Параметры электрических цепей переменного тока

Большинство потребителей электрической энергии работает на переменном токе. В настоящее время почти вся электрическая энергия вырабатывается в виде энергии переменного тока. Это объясняется преимуществом производства и распределения этой энергии. Переменный ток получают на электростанциях, преобразуя с помощью генераторов механическую энергию в электрическую. Основное преимущество переменного тока по сравнению с постоянным заключается в возможности с помощью трансформаторов повышать или понижать напряжение, с минимальными потерями передавать электрическую энергию на большие расстояния, в трехфазных источниках питания получать сразу два напряжения: линейное и фазное. Кроме того, генераторы и двигатели переменного тока более просты по устройству, надежней в работе и проще в эксплуатации по сравнению с машинами постоянного тока.

В электрических цепях переменного тока наиболее часто используют синусоидальную форму, характеризующуюся тем, что все токи и напряжения являются синусоидальными функциями времени. В генераторах переменного тока получают ЭДС, изменяющуюся во времени по закону синуса, и тем самым обеспечивают наиболее выгодный эксплуатационный режим работы электрических установок. Кроме того, синусоидальная форма тока и напряжения позволяет производить точный расчет электрических цепей с использованием метода комплексных чисел и приближенный расчет на основе метода векторных диаграмм. При этом для расчета используются законы Ома и Кирхгофа, но записанные в векторной или комплексной форме.

В современной технике широко используют разнообразные по форме переменные токи и напряжения: синусоидальные, прямоугольные, треугольные и др. Значение тока, напряжения, ЭДС в любой момент времени t называется мгновенным значением и обозначается малыми строчными буквами, соответственно

i = i(t); u = u(t); e = e(t).

Токи, напряжения и ЭДС, мгновенные значения которых повторяются через равные промежутки времени, называют периодическими, а наименьший промежуток времени, через который эти повторения происходят, называют периодом Т.

Если кривая изменения периодического тока описывается синусоидой, то ток называют синусоидальным. Если кривая отличается от синусоиды, то ток несинусоидальный.

В промышленных масштабах электрическая энергия производится, передается и расходуется потребителями в виде синусоидальных токов, напряжений и ЭДС,

При расчете и анализе электрических цепей применяют несколько способов представления синусоидальных электрических величин.

 Цепь с последовательным соединением элементов

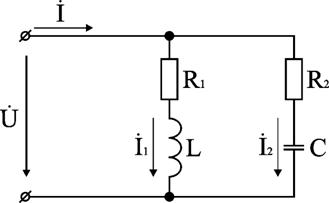 Цепь с параллельным соединением элементов

Уравнение и графики синусоидальных величин (период, частота, угловая частота, фаза, начальная фаза, сдвиг фаз)

В любой линейной цепи вне зависимости от вида элементов, входящих в цепь, гармоническое напряжение вызывает гармонический ток и, наоборот, гармонический ток порождает напряжения на зажимах этих элементов также гармонической формы. Обратим внимание, что индуктивности катушек и емкости конденсаторов предполагаются также величинами линейными.

В более общем случае можно сказать, что в линейных цепях при гармонических воздействиях все отклики имеют также гармоническую форму. Следовательно, в любой линейной цепи все мгновенные напряжения и токи имеют одну и ту же гармоническую форму. Если цепь содержит хотя бы несколько элементов, то синусоидальных кривых становится достаточно много, эти временные диаграммы накладываются друг на друга, чтение их сильно затрудняется, изучение становится предельно неудобным.

По указанным причинам изучение процессов, происходящих в цепях при гармонических воздействиях, производят не на кривых синусоидальной формы, а с помощью векторов, длины которых берутся пропорциональными максимальным значениям кривых, а углы, под которыми откладываются векторы, равными углам между началами двух кривых или началом кривой и началом координат. Таким образом, вместо временных диаграмм, занимающих много места, приводят их изображения в виде векторов, т. е. прямых линий со стрелками на концах, причем у векторов напряжения стрелки показывают заштрихованными, а у векторов тока оставляют незаштрихованными.

Совокупность векторов напряжений и токов в цепи называется векторной диаграммой. Правило отсчета углов на векторных диаграммах следующее: если необходимо показать вектор, отстающий от начального положения на некоторый угол, то поворачивают вектор на данный угол по часовой стрелке. Вектор, повернутый против часовой стрелки, означает опережение на указанный угол.

Например, на схеме рис. 1 показаны три временные диаграммы с одинаковыми амплитудами, но различными начальными фазами. Следовательно, длины векторов, соответствующих этим гармоническим напряжениям, должны быть одинаковыми, а углы — разными. Проведем взаимно перпендикулярные координатные оси, за начало отсчета примем горизонтальную ось с положительными значениями, в этом случае вектор первого напряжения должен совпадать с положительной частью горизонтальной оси, вектор второго напряжения — быть повернутым по часовой стрелке на угол ψ2, а вектор третьего напряжения — против часовой стрелки на угол(рис. 1).

Длины векторов зависят от выбранного масштаба, иногда их проводят произвольной длины с соблюдением пропорций. Поскольку максимальные и действующие значения всех гармонических величин отличаются всегда в одно и то же число раз (в √2= 1,41), то на векторных диаграммах можно откладывать как максимальные, так и действующие значения.

Временная диаграмма показывает значение гармонической функции в любой момент в соответствии с уравнением u = Umsinωt.На векторной диаграмме также можно показать значения в каждый момент времени. Для этого необходимо представить вектор вращающимся в направлении против часовой стрелки с угловой скоростью ω и брать проекцию этого вектора на вертикальную ось. Получившиеся длины проекций будут подчиняться закону u = Umsinωt и, следовательно, представлять мгновенные значения в том же масштабе. Направление вращения вектора против часовой стрелки считают положительным, а по часовой стрелке — отрицательным.

Рис.1 Рис.2

Рис.3

Графическое изображение синусоидальных величин

Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.

Любая синусоидальная величина характеризуется:

1. амплитудой;

2. угловой частотой;

3. начальной фазой.

При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.

При этом длина вектора равна амплитудному значению величины, угол между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью 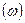. Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.

Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.

Совокупность нескольких векторов называется векторной диаграммой.

Электромагнитный процесс в электрической цепи называется периодическим, если значения токов и напряжений повторяются через равные промежутки времени. Время, через которое повторяются мгновенные значения величин, называются периодом T.

f(t ± kT) = f(t). (2.7)

Величина, обратная периоду, называется частотой. ;

,(2.8)

.

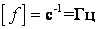Наиболее распространенным и важным видом периодических токов и напряжений являются синусоидальные (гармонические) токи и напряжения.

Мгновенное значение синусоидального тока записывается следующим образом:

, (2.9)

где I_m – амплитуда, или максимальное значение тока; w ? угловая или циклическая частота;

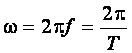, (2.10)

где ? фаза; ; Y_i – начальная фаза, [Y_i]= рад (или градус).

Аналогично записываются мгновенные значения других синусоидальных функций времени.

Для построения графиков обычно используют основные значения синуса. При Y_I ? 0 начинают построение с величин wt₀= ?Y_i, т.е., при Y > 0 график смещается влево от начала координат, а при Y_I < 0 – вправо на величину (рис. 2.3).

Разность начальных фаз двух синусоидальных функций одной частоты называется сдвигом их по фазе. Если Y₁ ?Y₂ = 0, синусоиды совпадают по фазе, а если Y₁ ?Y₂ = ±p, они находятся в противофазе.

 

---

Дата добавления: 2018-04-04; просмотров: 3178; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!