Тема 3.1. Приближенные аналитические методы решения задач теплопроводности
Метод дополнительных граничных условий в нестационарных задачах теплопроводности
Настоящая глава посвящена спектральным задачам, лежащим в основе всей аналитической теории краевых задач переноса. При использовании для решения таких задач метода разделения переменных (метода Фурье) возникает необходимость нахождения функций, удовлетворяющих дифференциальным уравнениям краевой задачи, полученным после разделения переменных в исходном уравнении. Такие функции известны лишь для классических дифференциальных уравнений (Штурма-Лиувилля, Бесселя, Лежандра и др.). Собственные числа находятся из граничных условий краевой задачи путём решения трансцендентных уравнений. При сложных дифференциальных уравнениях, когда неизвестны функции, удовлетворяющие им, трудности применения метода Фурье настолько возрастают, что во многих случаях он оказывается практически неприменим.
В настоящей работе для решения спектральных задач совместно с методом Фурье используются методы взвешенных невязок (ортогональный метод Бубнова-Галёркина). Важной особенностью является введение дополнительных граничных условий, необходимость которых объясняется появлением дополнительного неизвестного параметра 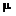 после разделения переменных в исходном дифференциальном уравнении. Дополнительные граничные условия выводятся из основного дифференциального уравнения путём его дифференцирования в граничных точках. Использование метода Бубнова-Галеркина позволяет находить высокой точности приближенные аналитические решения для всех тех краевых задач, уравнения (в частных производных) которых допускают разделение переменных. Такой подход значительно расширяет круг задач, решаемых с использованием метода Фурье, что связано с универсальностью метода Бубнова-Галеркина, при использовании которого на вид дифференциальных операторов не накладывается практически никаких условий. Это могут быть задачи с несимметричными и неоднородными граничными условиями первого, второго и третьего рода, с переменным начальным условием и физическими свойствами среды, задачи теплопроводности для многослойных конструкций и другие задачи.
после разделения переменных в исходном дифференциальном уравнении. Дополнительные граничные условия выводятся из основного дифференциального уравнения путём его дифференцирования в граничных точках. Использование метода Бубнова-Галеркина позволяет находить высокой точности приближенные аналитические решения для всех тех краевых задач, уравнения (в частных производных) которых допускают разделение переменных. Такой подход значительно расширяет круг задач, решаемых с использованием метода Фурье, что связано с универсальностью метода Бубнова-Галеркина, при использовании которого на вид дифференциальных операторов не накладывается практически никаких условий. Это могут быть задачи с несимметричными и неоднородными граничными условиями первого, второго и третьего рода, с переменным начальным условием и физическими свойствами среды, задачи теплопроводности для многослойных конструкций и другие задачи.
|
|
|
Тема 3.2. Применение приближенных аналитических методов.
Неограниченная пластина
(алгебраические координатные функции)
Рассмотрим методику определения собственных чисел, основанную на совместном использовании метода Фурье и методов взвешенных невязок. При таком подходе на первоначально принимаемое решение в виде простого алгебраического или тригонометрического полинома не накладывается никаких предварительных условий. Неизвестные коэффициенты решения определяются из выполнения основных и дополнительных граничных условий. Собственные числа находятся путём интегрирования невязки дифференциального уравнения Штурма-Лиувилля либо из условия ортогональности невязки к собственной функции.
|
|
|
В качестве конкретного примера рассмотрим задачу теплопроводности для бесконечно-протяжённой пластины при граничных условиях первого рода:

 ; (
; (  ;
;  ) (6.1)
) (6.1)
 ; (4.2)
; (4.2) 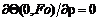 ; (4.3)
; (4.3)  , (6.4)
, (6.4)
где  – относительная избыточная температура;
– относительная избыточная температура; 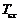 – температура пластины при
– температура пластины при  ;
;  – безразмерная координата;
– безразмерная координата;  – половина толщины пластины;
– половина толщины пластины; 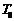 – начальная температура;
– начальная температура; 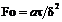 – число Фурье;
– число Фурье;  – коэффициент температуропроводности;
– коэффициент температуропроводности;  – время.
– время.
Следуя методу Фурье, решение задачи (6.1) – (6.4) принимается в виде:
 . (6.5)
. (6.5)
Подставляя (6.5) в (6.1), находим:
 .
.
Отсюда получаем следующие два обыкновенные дифференциальные уравнения:
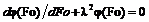 ; (4.6)
; (4.6)  , (6.7)
, (6.7)
где 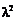 – некоторая постоянная.
– некоторая постоянная.
Решение уравнения (6.6), как известно, имеет вид:
 , (6.8)
, (6.8)
где  – неизвестный коэффициент.
– неизвестный коэффициент.
Уравнение Штурма-Лиувилля (6.7) представим следующим образом:
 , (6.9)
, (6.9)
|
|
|
где  .
.
Граничные условия для уравнения (6.9) согласно (6.3), (6.4) будут:
 ; (6.10)
; (6.10)  . (6.11)
. (6.11)
Решение задачи (4.9) – (4.11) разыскивается в виде следующего ряда:
 , (6.12)
, (6.12)
где 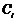 (
(  ) – неизвестные постоянные, определяемые из граничных условий задачи;
) – неизвестные постоянные, определяемые из граничных условий задачи;  – координатные функции (алгебраический или тригонометрический полином).
– координатные функции (алгебраический или тригонометрический полином).
Если ограничиться, например, пятью членами ряда (6.12) (  ), то будем иметь пять неизвестных коэффициентов
), то будем иметь пять неизвестных коэффициентов 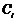 (
(  ), а граничных условий только два (6.10), (6.11). В связи с чем, необходимо добавить ещё три дополнительных граничных условия, которые находятся из условия (6.10) и из уравнения (6.9) путём выполнения этого уравнения, а также соотношений, полученных после взятия производных от него различного порядка в граничных точках
), а граничных условий только два (6.10), (6.11). В связи с чем, необходимо добавить ещё три дополнительных граничных условия, которые находятся из условия (6.10) и из уравнения (6.9) путём выполнения этого уравнения, а также соотношений, полученных после взятия производных от него различного порядка в граничных точках  и
и  . Такие дополнительные граничные условия будут иметь вид:
. Такие дополнительные граничные условия будут иметь вид:
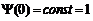 ; (6.13)
; (6.13)  ; (6.14)
; (6.14)  . (6.15)
. (6.15)
Необходимость введения дополнительных граничных условий объясняется тем, что в уравнениях (6.6), (6.7) появляется новый неизвестный параметр  , который находится из характеристического уравнения, получаемого в результате подстановки (6.12) в дифференциальное уравнение (6.9). В зависимости от числа членов ряда (6.12) вводится соответствующее число дополнительных граничных условий и в итоге получается соответствующее количество собственных чисел.
, который находится из характеристического уравнения, получаемого в результате подстановки (6.12) в дифференциальное уравнение (6.9). В зависимости от числа членов ряда (6.12) вводится соответствующее число дополнительных граничных условий и в итоге получается соответствующее количество собственных чисел.
|
|
|
Подставляя (6.12) в (6.10), (6.11), (6.13) – (6.15), получим пять алгебраических линейных уравнений относительно пяти неизвестных 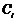 . При этом каждое из неизвестных
. При этом каждое из неизвестных  ,
,  ,
,  входит лишь в одно уравнение, из которого они легко определяются. Все эти уравнения получаются из граничных условий при
входит лишь в одно уравнение, из которого они легко определяются. Все эти уравнения получаются из граничных условий при  (условия (6.10), (6.13), (6.15)). Относительно неизвестных
(условия (6.10), (6.13), (6.15)). Относительно неизвестных  ,
,  необходимо решить два взаимосвязанных алгебраических линейных уравнения. В итоге для всех искомых неизвестных постоянных будем иметь следующие значения:
необходимо решить два взаимосвязанных алгебраических линейных уравнения. В итоге для всех искомых неизвестных постоянных будем иметь следующие значения:
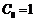 ;
;  ;
;  ;
;  ;
;  .
.
Подставляя найденные значения 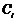 в (6.12), получаем:
в (6.12), получаем:
 . (6.16)
. (6.16)
Для определения первого собственного числа найдём интеграл взвешенной невязки уравнения (6.9), т. е.
 . (6.17)
. (6.17)
Подставляя (6.16) в (6.17), относительно  получаем характеристическое уравнение, из которого находим
получаем характеристическое уравнение, из которого находим  . Точное значение первого собственного числа
. Точное значение первого собственного числа  [49].
[49].
Для уточнения первого собственного числа составим невязку уравнения (4.9) и потребуем ортогональность невязки к собственной функции (6.16), т. е.
 . (6.18)
. (6.18)
Подставляя (6.16) в (6.18), относительно  получаем характеристическое уравнение:
получаем характеристическое уравнение:
 .
.
Его решение  .
.
Следовательно, выполнение требования ортогональности невязки уравнения (6.9) к собственной функции (6.16) приводит к существенному уточнению первого собственного числа.
Для получения первых двух собственных значений вводятся следующие дополнительные граничные условия, получаемые из уравнения (6.9):
 ; (4.19)
; (4.19)  . (6.20)
. (6.20)
В итоге всего имеем семь граничных условий – два основных (4.10), (4.11) и пять дополнительных (6.13) – (6.15), (6.19), (6.20). Следовательно, для определения коэффициентов 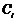 (
( 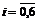 ) следует использовать семь членов ряда (6.12).
) следует использовать семь членов ряда (6.12).
Подставляя (6.12) при  во все граничные условия задачи, относительно
во все граничные условия задачи, относительно 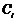 получим семь алгебраических уравнений. Пять из этих уравнений разделяются, т. е. в одно уравнение входит лишь одно неизвестное. Таким путём находятся неизвестные:
получим семь алгебраических уравнений. Пять из этих уравнений разделяются, т. е. в одно уравнение входит лишь одно неизвестное. Таким путём находятся неизвестные:
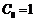 ;
;  ;
; 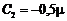 ;
;  ;
;  .
.
Неизвестные  ,
,  находятся из системы двух алгебраических уравнений, составленных из граничных условий при
находятся из системы двух алгебраических уравнений, составленных из граничных условий при  , т. е. из граничных условий (6.11), (6.14). Из решения этой системы находим:
, т. е. из граничных условий (6.11), (6.14). Из решения этой системы находим:
 ;
;  .
.
После подстановки коэффициентов 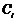 в (6.12) составляется интеграл взвешенной невязки уравнения (6.9). Отсюда для определения собственных чисел получается следующее характеристическое уравнение:
в (6.12) составляется интеграл взвешенной невязки уравнения (6.9). Отсюда для определения собственных чисел получается следующее характеристическое уравнение:
 .
.
Его решение  ;
;  .
.
Для уточнения первых двух собственных чисел требуется ортогональность невязки уравнения (6.9) к собственной функции (6.12) при  . Для определения собственных чисел получается характеристическое уравнение вида:
. Для определения собственных чисел получается характеристическое уравнение вида:

 .
.
Его решение  ;
;  .
.
Ввиду того, что уравнение Штурма-Лиувилля (6.9) удовлетворяется лишь при некоторых дискретных значениях  (собственных значениях, образующих спектр), остальные корни уравнения (три корня) следует отбросить, как не удовлетворяющие этому уравнению (в чём можно убедиться непосредственной подстановкой).
(собственных значениях, образующих спектр), остальные корни уравнения (три корня) следует отбросить, как не удовлетворяющие этому уравнению (в чём можно убедиться непосредственной подстановкой).
Как видно, первое собственное число до девятого знака совпадает с точным его значением. Точное значение второго собственного числа [49]:
 .
.
Собственные функции находятся из (6.12).
Для получения трёх собственных чисел ко всем имеющимся граничным условиям добавляются дополнительные граничные условия вида:
 ;
;  ;
;  ;
;  ;
;  ;
;  .
.
В данном случае для первых трех собственных чисел получаются следующие значения (найдены с учётом ортогональности невязки уравнения (6.9) к функции (6.12))  ;
;  ;
; 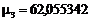 . Отметим, что точное значение третьего собственного числа составляет
. Отметим, что точное значение третьего собственного числа составляет  [49].
[49].
Для получения пяти собственных чисел используются следующие дополнительные граничные условия:
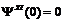 ;
;  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;  ; (6.21)
; (6.21)
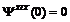 ;
;  .
.
В этом случае имеем  ;
;  ;
;  ;
;  ;
; 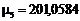 . Точные значения четвёртого и пятого собственных чисел
. Точные значения четвёртого и пятого собственных чисел  ;
;  .
.
Подставляя (6.8), (6.12) в (6.5), для каждого собственного числа будем иметь частные решения вида:
 . (
. (  )
)
Каждое частное решение точно удовлетворяет граничным условиям (6.3), (6.4) и приближённо (в пятом приближении) удовлетворяет уравнению (6.1) на отрезке  . Однако ни одно из этих частных решений, в том числе и их сумма
. Однако ни одно из этих частных решений, в том числе и их сумма
 , (6.22)
, (6.22)
не удовлетворяют начальному условию (6.2).
Для выполнения начального условия составляется его невязка и требуется ортогональность невязки к каждой собственной функции, т. е.
 . (
. (  ) (6.23)
) (6.23)
Определяя интегралы в (4.23), для нахождения коэффициентов  (
(  ) получаем систему пяти алгебраических линейных уравнений. Её решение:
) получаем систему пяти алгебраических линейных уравнений. Её решение:
 ;
;  ;
;  ;
; 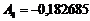 ;
; 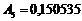 .
.
Приведённые здесь коэффициенты  найдены из уточнённых значений собственных чисел (путём требования ортогональности невязки уравнения (6.9) к функции (6.12)).
найдены из уточнённых значений собственных чисел (путём требования ортогональности невязки уравнения (6.9) к функции (6.12)).
Таблица 6.1
Собственные числа для различных приближений в сравнении
с точными их значениями
| Число прибли- жений | Собственные числа | ||||

| 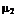
| 
| 
| 
| |
| 1 | 2,5 2,4677419355 | – | – | – | – |
| 2 | 2,46698193 2,46740110 | 21,79447220 22,26983 | – | – | – |
| 3 | 2,4674011011 2,4674011001 | 22,2018150 22,2066100 | 61,465669 62,055342 | – | – |
| 4 | 2,4674011003 2,4674011002 | 22,2066102 22,2066098 | 61,680400 61,685017 | 120,5326 120,9039 | – |
| 5 | 2,4674011 2,4674011002 | 22,2066099 22,206610 | 61,684934 61,685023 | 120,9750 120,9024 | 238,095 201,058 |
| Точные значе- ния [49] | 2,4674011003 | 22,2066099 | 61,685026 | 120,9026 | 199,859 |
Собственные числа для различных приближений в сравнении с точными их значениями приведены в табл. 6.1 (для каждого приближения верхняя строка – без ортогональности, нижняя – с ортогональностью невязки уравнения (6.9) к функции (6.12)).
Результаты расчётов безразмерных температур по формуле (6.22) в сравнении с точными их значениями [49] представлены на графиках рис. 6.1, 6.2.
Анализ результатов расчётов позволяет заключить, что в пятом приближении температуры, полученные по формуле (6.22), в диапазоне чисел Фурье  практически совпадают с точными их значениями.
практически совпадают с точными их значениями.
Таким образом, в методе Бубнова-Галеркина требуется удовлетворить условиям ортогональности невязки первым 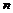 функциям некоторой полной в данной области системы линейно-независимых функций. Из теории рядов Фурье [28] следует, что равенство невязки нулю (а это имеет место при точном решении уравнения (6.9)) равносильно требованию ортогональности ее ко всем функциям
функциям некоторой полной в данной области системы линейно-независимых функций. Из теории рядов Фурье [28] следует, что равенство невязки нулю (а это имеет место при точном решении уравнения (6.9)) равносильно требованию ортогональности ее ко всем функциям  системы. Имея, однако, в своем распоряжении лишь
системы. Имея, однако, в своем распоряжении лишь 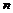 членов полинома (6.12) (или
членов полинома (6.12) (или 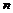 постоянных
постоянных 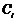 ) мы можем удовлетворить только
) мы можем удовлетворить только 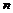 условиям ортогональности, что и приводит лишь к приближенному решению.
условиям ортогональности, что и приводит лишь к приближенному решению.

|
Рис. 6.1 Изменение относительной избыточной температуры в пластине. –———— – точное решение [49];  – по формуле (6.22) – по формуле (6.22)
|

|
Рис. 6.2 Изменение температуры в пластине. –———— – точное решение [49];  – по формуле (6.22) – по формуле (6.22)
|
Следует отметить высокую точность определения собственных чисел по сравнению с другими методами совместного использования точных и приближенных методов. К числу таких методов относятся: совместное использование интегральных преобразований Лапласа и метода Бубнова-Галеркина [83], методов Фурье и Л.В. Канторовича [27, 28, 46], методов Фурье и Бубнова-Галеркина (без использования дополнительных граничных условий). Все эти методы для одних и тех же задач приводят к мало отличающимся результатам. В качестве конкретного примера в таблице 6.2 приведены собственные числа для четвертого и пятого приближений, полученные при решении задачи (6.1) – (6.4) путем совместного использования интегральных преобразований Лапласа и метода Бубнова-Галеркина.
Таблица 6.2
Дата добавления: 2018-02-28; просмотров: 743; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
