Вычисление обратной матрицы с помощью присоединённой матрицы
Теорема.
Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной.
Замечание.
Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.
25.Свойства линейных пространств.
1) В каждом линейном пространстве существует только один нулевой элемент.
2) Для каждого элемента существует только один противоположный элемент.
3) Для каждого х Î L верно 0×х = 0
4) Для каждого a Î R и оÎ L верно a×о=о
5) Если a×х = о, то a = 0 или х= о
6) (-1) х = -х
Линейные преобразования.
Определение: Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу хÎ L по некоторому правилу ставится в соответствие элемент АхÎ L.
Определение: Преобразование А называется линейным, если для любых векторов хÎ L ихÎ L и любого a верно:
A(х+у) = Aх+Aу
A(aх) = aAх
27. (теорема Кронекера-Капелли). Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.
Доказательство.
- Необходимость: пусть система (2.2) совместна и
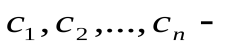ее решение. Тогда
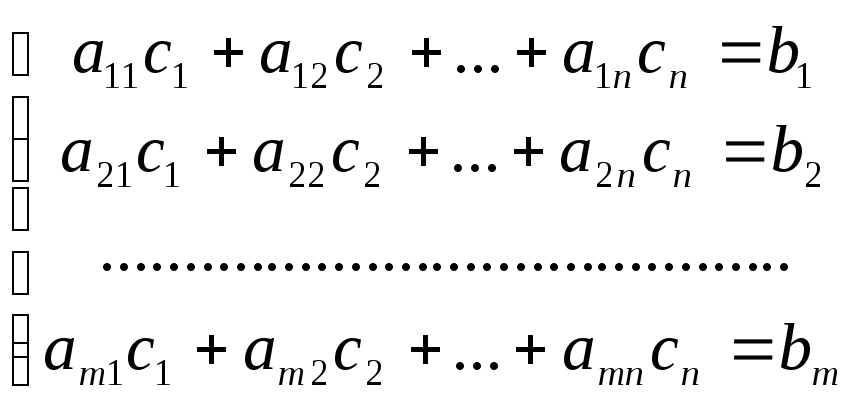, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть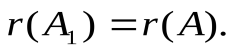 
|
|
|
- Достаточность: если
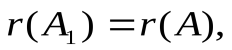то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации 
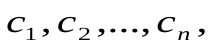то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
Общее решение однородной линейной системы.
Рассмотрим однородную линейную систему
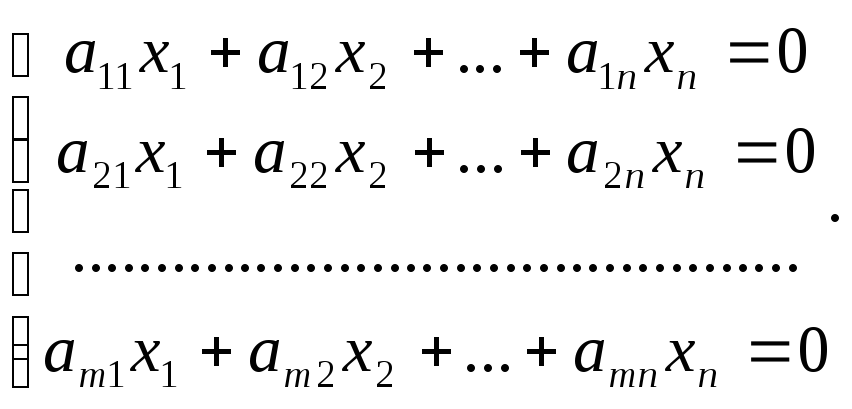. (4.2)
Отметим, что такая система всегда совместна, поскольку имеет нулевое решение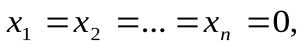 
называемое тривиальным.
Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первыхrуравнений. Тогда оставшиесяm–rуравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первыеrуравнений:
. 
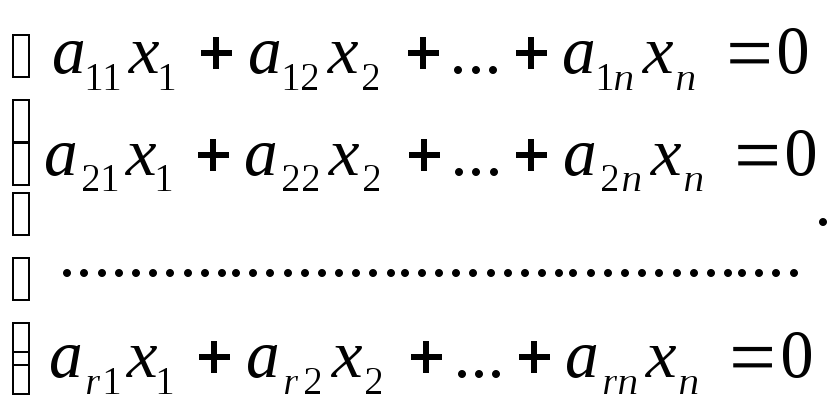
Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:
|
|
|
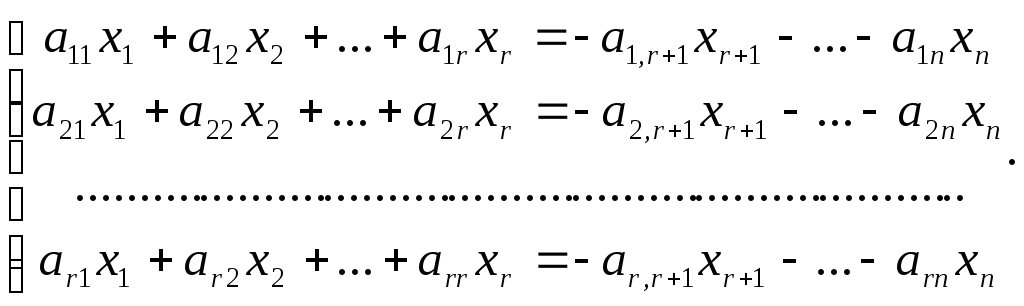(4.3)
Эта система будет иметь единственное решение относительно неизвестных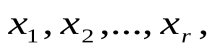 
выражающее их через остальные неизвестные ( 
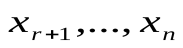), которым можно придавать любые произвольные значения. Таким образом, система (4.2) приr<nявляется неопределенной.
Определение: Линейное преобразование называется тождественным, если оно преобразует элемент линейного пространства сам в себя.
Е х= хКасательная к графику функции График дифференцируемой в точке х0 функции f вблизи х0 практически не отличается от отрезка касательной, а значит, он близок к отрезку секущейl, проходящей через точки(х0; f(х0)) и (х0 +?x;f (х0+?x)). Любая из таких секущих проходит через точку А(х0; f(х0)) графика
Дата добавления: 2018-02-28; просмотров: 260; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!