Методы вычисления обратной матрицы

Стр 1 из 4Следующая ⇒

Признак коллинеарности (параллельности) векторов.Если векторы коллинеарны, то их соответствующие координаты пропорциональны и обратно.Если коэффициент пропорциональности положителен, то векторы равнонаправлены; если отрицателен — противоположно направлены. Абсолютное значение X выражает отношение длин.Замечание. Если одна из координат вектора равна нулю, то пропорцию (1) надо понимать в том смысле, что соответствующая координата вектора тоже равна нулю. 2.Определение. Линейной комбинацией векторов a1, ..., an с коэффициентами x1, ..., xn называется вектор x1a1 + ... + xnan. Определение. Линейная комбинация x1a1 + ... + xnan называется тривиальной, если все коэффициенты x1, ..., xnравны нулю. Определение. Линейная комбинация x1a1 + ... + xnan называется нетривиальной, если хотя быбы один из коэффициентов x1, ..., xn не равен нулю. Определение. Вектора a1, ..., an называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору. То есть вектора a1, ..., an линейно независимы если x1a1 + ... + xnan = 0 тогда и только тогда, когда x1 = 0, ..., xn = 0. Определение. Вектора a1, ..., an называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору. Свойства линейно зависимых векторов: Для 2-х и 3-х мерных векторов. Два линейно зависимые вектора - коллинеарные. (Коллинеарные вектора - линейно зависимы.) . Для 3-х мерных векторов. Три линейно зависимые вектора - компланарные. (Три компланарные вектора - линейно зависимы.) Для n -мерных векторов.1 вектор всегда линейно зависимы. 3. n + -мерные арифметические векторы n-мерным арифметическим вектором называется упорядоченная совокупность n действительных чисел, а числа, входящие в эту совокупность, называются координатами вектора. Число координат вектора называется его размерностью. Если все координаты вектора равны нулю, то вектор называется нулевым и обозначается 0 или . Если соответствующие координаты векторов и равны, то векторы называютсяравными: Таким образом, при сложении или вычитании векторов складываются или вычитаются их одноименные координаты. При умножении вектора на число каждая координата вектора умножается на это число. Базисом данной системы векторов (максимальной линейно независимой подсистемой) называется такая подсистема, векторы которой линейно независимы, а любой другой вектор системы является их линейной комбинацией.Система векторов может иметь несколько базисов. При этом все они содержат одинаковое количество векторов.Рангом системы векторов называется число векторов в любом базисе системы. Другими словами, ранг системы векторов равен максимальному числу линейно независимых векторов системы.Базисом n-мерного векторного пространства называется совокупность n линейно независимых векторов этого пространства.Координатами вектора в данном базисе называется упорядоченный набор коэффициентов, с помощью которых этот вектор выражается через базисные векторы.Пусть е = - базис и . Упорядоченный набор {х, у, z} - это координаты вектора в базисе е. Обозначение в= {х, у, z}. Если используется несколько базисов, то обозначают в= {х, у, z}е. 4. Даны точки A1(x1;x2) и A2(y1;y2), требуется найти координаты x, y, точки K, делящей отрезок AB в отношении.A1K:KA2=m1:m2 Решение производится формулами Если отношение m1:m2 обозначить буквой λ, тогда формула примет несимметричный вид. Замечание. 1. Выражение «точкиK, делящей отрезокA1A2в отношенииm1:m2» означает, что отношениеm1:m2равно отношению отрезковA1K:KA2, взятых именно в этом порядке. 2. Пусть точкаKделит отрезокA1A2внешним образом, т.е. лежит на продолжение отрезкаA1A2, тогда формулы сохраняют силу, если величинеm1:m2=λприписать отрицательный знак. 18.Поверхности вращения. Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращенияс осью вращения d. Если уравнение поверхности в прямоугольной системе координат имеет вид: F(x2 + y2, z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz. Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу, F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох. Запишем уравнения поверхностей вращения для некоторых частных случаев: 1) — эллипсоид вращения 2) — однополостный гиперболоид вращения 3) — двуполостный гиперболоид вращения 4) — параболоид вращения Аналогично могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох или Оу. Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже: Сфера: 19.Цилиндрические поверхности. Определение. Поверхность называется цилиндрической, если она образована параллельным перемещением некоторой прямой, называемой образующей, вдоль некоторой кривой, называемой направляющей. Пример. Возьмем в качестве направляющей окружность. Рассмотрим множество прямых параллельных друг другу и расположенных под некоторым углом к плоскости в которой лежит окружность и проходящих через каждую точку окружности.Теорема. Если уравнение является уравнением кривой на координатной плоскости Оху, то это же уравнение является уравнением цилиндрической поверхности, направляющей которой служит данная кривая, а образующей является прямая, проходящая через точку данной кривой и параллельной оси Оz. Доказательство. Пусть точка лежит на кривой . Тогда . Так как это уравнение не содержит переменной z, то для любого числа координаты точки также удовлетворяют этому уравнению. Иначе, любое решение этого уравнения есть координаты точки, лежащей на прямой, параллельной оси Оz и проходящей через точку кривой на плоскости Оху. Очевидно, верно и обратное. 20.Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением : (1) Уравнение (1) называется каноническим уравнением эллипсоида. Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h , где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями (2) Исследуем уравнения (2) при различных значениях h. 1) Если > c (c>0), то и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует. 2) Если , то и линия (2) вырождается в точки (0; 0; + c ) и (0; 0; - c ) (плоскости касаются эллипсоида). 3) Если , то уравнения (2) можно представить в виде откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями и . При уменьшении значения и увеличиваются и достигают своих наибольших значений при , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями и . Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz . Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферо й . Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением (3) Уравнение (3) называется каноническим уравнением однополосного гиперболоида. Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy ( y=0) и Oyx (x=0).Получаем соответственно уравнения и из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy . Линия, получающаяся в сечении, определяется уравнениями или (4) из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями и , достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании величины a* и b* возрастают бесконечно. Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy. Величины a, b, c называются полуосями однополосного гиперболоида.3. Двуполостный гиперболоид. Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением (5) Уравнение (5) называется каноническим уравнением двуполостного гиперболоида. Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения и из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями или (6) из которых следует, что при >c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями и . При увеличении величины a* и b* тоже увеличиваются. При уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости касаются данной поверхности). При уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует. Величина a, b и c называются полуосями двуполостного гиперболоида. Эллиптический параболоид. Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением (7) где p>0 и q>0. Уравнение (7) называется каноническим уравнением эллиптического параболоида. Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения и из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями или (8) из которых следует, что при плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями и . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскостьz=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет. Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши. Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).

Гиперболический параболоид.

Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением

(9)

где p>0, q>0.

Уравнение (9) называется каноническим уравнением гиперболического параболоида.

Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение

(10)

из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.

рассмотрим сечение данного параболоида плоскостью Oyz (x=0).

Получаем уравнение

из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения

из которых следует, что при любом h в сеченииполучается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).

Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения

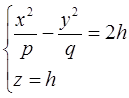или

из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых

точка (0;0;0) называется вершиной параболоида; числа p и q – его параметр

21.Обратная матрица A⁻¹ — матрица, произведение которой на исходную матрицу A равно единичной матрице E:

A·A^-1 = A^-1·A = E

Замечание.

Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.

Свойства обратной матрицы

●

det(A^-1) =	1
	det(A)

●

(A·B)^-1 = A^-1·B^-1

●

(A^-1)^T = (A^T)^-1

●

(kA)^-1 =	A^-1
	k

●

(A^-1)^-1 = A

Методы вычисления обратной матрицы

Дата добавления: 2018-02-28; просмотров: 288; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!