Расчет конструкций методом конечных элементов
Метод конечных элементов
Появление современных вычислительных средств отразилось не только на изменении алгоритмов классических методов расчетов, таких, как метод сил, метод перемещений и др., но и на формировании новых идей и методов. Изменился и подход к оценке эффективности приемов расчета сооружений, изменились критерии, позволяющие формировать требования, предъявляемые к современным методам. Так, если раньше при применении классических методов расчетов статически неопределимых шарнирно-стержневых систем трудоемкость расчетов определялась числом лишних неизвестных, то в настоящее время основные трудности расчетов подобных систем связаны с необходимостью общения человека с машиной, с определенной ограниченностью существующих алгоритмических языков. При этом возникла необходимость создания таких алгоритмов, которые, может быть, и приводят к более сложному математическому описанию, но обладают большей логической четкостью и ясностью.
Одним из таких методов, эффективно развиваемых в последнее время, является МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ (МКЭ) [1].
Название этого метода в некоторой мере предопределяет его сущность, так как при его использовании конструкция, тем или иным путем разбивается на отдельные элементы конечной длины и достаточно простой конфигурации, напряженно-деформированное состояние которых предварительно подробно изучено. Сопряжение элементов осуществляется путем удовлетворения условий равновесия и неразрывности перемещений (одинаковая величина перемещения в узле для всех соединенных с данным узлом элементов). Поведение каждого элемента описывается конечным числом обобщенных координат. Такая формулировка расчета объединяет подход как к объектам строительной механики стержневых систем, так и к объектам теории упругости, что позволяет найти эффективные методы расчета реальных конструкций, в которых обычно соединены (чаще всего сварены между собой) стержни, плиты, пластины, оболочки и т.д.
|
|
|
При использовании МКЭ представляется возможным четко сформулировать три группы уравнений, как это сделано в теории упругости:
1) статические, описывающие равновесное состояние системы;
2) геометрические, устанавливающие связь между деформациями и перемещениями;
3) физические, связывающие между собой силы и деформации.
При рассмотрении стержневых систем МКЭ является точным методом.
Алгоритм расчета усилий в стержнях плоской фермы методом конечных элементов
Алгоритм составлен на основе применения теории матриц к расчету ферм [1].
Рассмотрим произвольную плоскую стержневую систему. В первую очередь, необходимо описать структуру решетки системы, пронумеровав все узлы фермы и ее стержни. Для описания структуры составляется структурная матрица -S , в которой в каждом ее столбце находятся только два числа: 1 и -1, причем 1 располагается в строке, номер которой совпадает с началом стержня, а -1 - в строке, номер которой совпадает с номером узла, к которому примыкает конец стержня. За начало стержня принимается тот его конец, который примыкает (присоединяется) к меньшему по номеру узлу. В каждой строке структурной матрицы (а строка соответствует узлу, совпадающему с ней по номеру) значащие числа характеризуют номера элементов, соединяемых в узле, причем 1 подчеркивает то, что к узлу подходит начало стержня, а -1 - что к узлу подходит конец стержня. Далее следует сформировать матрицы - столбцы координат узлов фермы:
|
|
|
, (3.49)
где i - номер соответствующего узла,
Xi и Yi - соответственно координаты X и Y узла в выбранной системе координат.
Общая матрица - столбец координат узлов фермы:
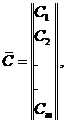(3.50)
|
|
|
где m - число узлов фермы.
Матрица проекций длин элементов фермы:
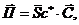(3.51)
где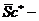 
транспонированная матрица 
.
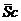(Транспонирование - преобразование исходной матрицы, состоящее в замене строк столбцами при сохранении их нумерации). Элементами матрицы проекций являются матрицы - столбцы, два элемента каждого из которых i-го стержня дают проекции:
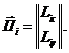(3.52)
Длины стержней определяются выражением:
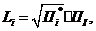(3.53)
где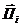 
- матрица проекций стержня.
- транспонированная матрица из .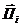
Векторы направляющих косинусов стержней:
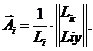(3.54)
По длине элемента фермы нормальная сила постоянна:
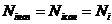. (3.55)
|
|
|
Построим вектор внешних нагрузок
(3.56)
элементами которого являются матрицы – столбцы -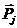 
, определяющие проекции внешних сил, действующих на узлы, например, для j-го узла имеем:
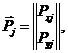(3.57)
где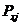 
и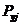 
- проекции внешних сил, действующих на j-й узел, на соответствующие координатные оси. Выражение, устанавливающее связь между внутренними усилиями и внешними силами, при этом будет следующее:
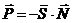, (3.58)
где 
- матрица – столбец, элементами которой являются искомые усилия в стержнях фермы;
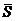- матрица, получаемая из структурной матрицы 
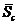путем замены элементов 1 на соответствующие векторы направляющих косинусов стержней, а элементов (-1) матрицы 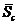на соответствующие векторы направляющих косинусов с обратным знаком. Для определения неизвестных усилий в стержнях из вектора 
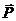следует исключить элементы матрицы, соответствующие опорным связям системы, и таким путем получить вектор 
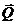. Tаким же образом из матрицы 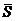необходимо исключить строки, соответствующие опорным узлам фермы. При этом для узла с шарнирно-неподвижным опиранием удаляются обе строки, а для узла с шарнирно-подвижным опиранием удалить одну строку. В результате таких преобразований получаем матрицу 
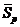. Тогда вектор усилий находится решением матричного уравнения:
(3.59)
Из уравнения (2.59) матрица столбец может быть определена:
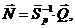(3.60)
где 
- обратная матрица относительно .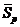
Дата добавления: 2018-02-28; просмотров: 694; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!