Уравнения гармонических колебаний, графики смещения скорости и ускорения, фаза
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия - достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Основное уравнение динамики гармонических колебаний. Решение уравнения.
Второй закон Ньютона позволяет, в общем виде, записать связь между силой и ускорением, при прямолинейных гармонических колебаниях материальной точки (или тела) с массой m.
Т.к. исходя из второго закона 
, можно записать:
где Fx – проекция силы на направление х. Из формулы следует, что сила F пропорциональна х и всегда направлена к положению равновесия (поэтому ее и называют возвращающей силой). Период и фаза силы совпадают с периодом и фазой ускорения.
|
|
|
Примером сил удовлетворяющих формуле являются упругие силы. Силы же, имеющие иную природу, но удовлетворяющие ф-ле, называются квазиупругими. Квазиупругая сила:
где k – коэффициент квазиупругой силы.
Сравнивая ф-лы, видим, что 
.
В случае прямолинейных колебаний вдоль оси х, проекция ускорения на эту ось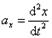 
.
Подставив выражения для ax и Fx во второй закон Ньютона, получим основное уравнение динамики гармонических колебаний, вызываемых упругими или квазиупругими силами:
или 
; 
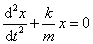, тогда
Решением этого уравнения всегда будет выражение вида:
,т.е. смещение груза под действием упругой или квазиупругой силы является гармоническим колебанием, происходящим по синусоидальному закону.
Круговая частота незатухающих колебаний 
, но, т.к. , тогда , отсюда
то есть чем больше жесткость пружины k, тем меньше период (больше частота), а чем больше масса, тем период колебаний больше.
Маятники математический и физический, пружинный. Их уравнения движения.
Математический маятник - это материальная точка, подвешенная на тонкой нерастяжимой и невесомой нити.
|
|
|
Период колебаний математического маятника зависит от его длины, определяется по формуле
Пружинный маятник - это груз, прикрепленный к пружине, массой которой можно пренебречь.
Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости.
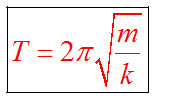
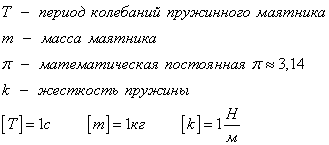
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
Тогда период колебаний математического маятника будет равен:
48.Затухающие колебания. Частота собственных колебаний ω0, затухающих колебаний ω, условный период Тусл.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Период затухающих колебаний вычисляют по формуле
Частота собственных колебаний:
Частота затухающих колебаний ω:
Дата добавления: 2018-02-28; просмотров: 2611; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!