ОЦЕНКА ПОГРЕШНОСТИ ИЗМЕРЕНИЯ С ПОМОЩЬЮ ДАТЧИКОВ
ДЕФОРМАЦИЙ ИНТЕГРАЛЬНОГО ТИПА КРУТЯЩЕГО МОМЕНТА НА ВАЛАХ И РОТОРАХ
| Д |
ля оценки погрешности измерения крутящего момента на роторах нефтеперекачивающих агрегатов с помощью датчиков деформаций интегрального типа (ДДИТ) необходимо получить границы доверительного интервала тарировочной зависимости, связывающей амплитуду касательных напряжений tg и число циклов нагружения Ng тарировочного образца с размещенным (наклеенным) на нем датчиком. Прежде чем решать данную задачу, рассмотрим причины возникновения разброса экспериментальных точек тарировочной зависимости. Анализируя методы регистрации напряжений и поврежденности деталей с помощью ДДИТ, изложенные в работах [3, 4], основными причинами вышеотмеченного разброса являются: погрешность регистрации показаний ДДИТ; флуктуация в определенных пределах свойств ДДИТ, влияющая на чувствительность датчика к накопленным пластическим деформациям в процессе его циклического деформирования; вариация физико-механических свойств тарировочных образцов и усталостных характеристик их материала.
В процессе построения тарировочной зависимости, связывающей амплитуду касательных напряжений g и число циклов нагружения Ng , реакция на ДДИТ устанавливается путем осмотра изготовленного из материала ротора тарировочного образца с ДДИТ под микроскопом [1]. В ходе реализации методики тарирования, при прерывании испытаний для осмотра датчиков, число циклов нагружения Ng известно точно (по счетчику циклов), диаметр рабочей части образца с ДДИТ, на которой фиксируется граница реакции на датчике, измеряется микрометром с погрешностью ±0,01мм. Действующие в этом сечении касательные напряжения (tgj) можно рассчитать по формуле
| . |
 (1)
(1)
Относительная погрешность задания на экспериментальном стенде [1] величины крутящего момента составляет pT / T = 0,006 (pT - абсолютная погрешность измерения T). Диаметр рабочей части используемых в эксперименте тарировочных образцов не превышает 10мм. Поэтому относительная погрешность измерения диаметра сечения образца, до которого распространилась реакция на датчике, pd / d = 0,01 / 10 = 0,001. Изложенное позволяет оценить погрешность измерения касательного напряжения tg в процессе проведения тарировочных испытаний на стенде.
Воспользуемся зависимостью (1) для расчета величины tgj в сечении тарировочного образца, определяемого диаметром dj. На основании результатов работы [6], ошибка pt результатов измерения tgj может быть вычислена по формуле
 . (2)
. (2)
После дифференцирования (1) и перехода к относительной ошибке измерения, на основе (2) получим
 . (3)
. (3)
Значения ( pT / T) и ( pd / dj) были определены выше, подставляя их в (2), установим
pt / tgj = 0,0067, то есть погрешность измерения tgj определяется погрешностью задания при тарировочных испытаниях величины T. Результаты калибровки ДДИТ, отраженные на рис. 4 [2], свидетельствуют о более высоком разбросе экспериментальных точек тарировочной зависимости. Аналогичная ситуация наблюдалась и ранее, при тарировании ДДИТ в условиях испытания образцов при изгибе [3, 4]. Обратимся к математическому описанию тарировочной кривой в форме (зависимость (2) [2]):
 , (4)
, (4)
где Ng – число циклов нагружения образца до реакции ДДИТ; tg – амплитуда касательного напряжения; Пg – величина поврежденности материала образца, соответствующая появлению реакции на ДДИТ; tbg – аналог предела прочности материала датчика; tr – предел выносливости материала образца при кручении с коэффициентом асимметрии цикла r.
Если калибровка ДДИТ осуществляется на одном образце, то величины tbg, tr являются детерминированными. Тогда помимо погрешности, вносимой неточностью измерения tgj, на разброс экспериментальных точек при тарировке ДДИТ будет оказывать влияние случайная природа величины пg, отражающей процесс накопления повреждений в материале датчика. Отметим, что при построении границ доверительного интервала тарировочной зависимости на основе обработки данных усталостных испытаний образцов зависимости [2], разброс результатов, следуя работам [3, 4], определяется, в первую очередь, случайной природой предела выносливости материала образца(tr). В общем случае Пg и tr являются независимыми случайными величинами со своими законами распределения. В то же время из анализа формулы (4) следует, что параметры Пg и tr присутствуют всегда вместе в виде произведения (tn= Пg×tr). Поэтому при разработке алгоритма определения границ доверительного интервала тарировочной зависимости достаточно считать случайной величину tn. В рассматриваемом варианте обработки экспериментальных данных, принимая величину tr детерминированной, определим характеристики случайной величины Пg, с учетом которых построим доверительный интервал тарировочной зависимости.
При решении задачи воспользуемся найденными в работе [2] значениями параметров tbg, tr и K зависимости (4). Величина же Пg, рассчитанная как Пg = tn / tr, в этом случае является лишь точечной оценкой случайной величины Пg. С целью определения статистических характеристик случайной величины Пg воспользуемся имеющейся совокупностью экспериментальных данных  , полученных в процессе тарирования ДДИТ [2] и математическим описанием (4). Эта зависимость при фиксированных и известных на момент решения задачи параметрах tbg, tr и K справедлива для каждой j-той точки, определяемой координатами
, полученных в процессе тарирования ДДИТ [2] и математическим описанием (4). Эта зависимость при фиксированных и известных на момент решения задачи параметрах tbg, tr и K справедлива для каждой j-той точки, определяемой координатами  . Воспользовавшись данным обстоятельством, преобразуем выражение (4), разрешив его относительно величины Пg º Пgj:
. Воспользовавшись данным обстоятельством, преобразуем выражение (4), разрешив его относительно величины Пg º Пgj:
 , (5)
, (5)
где  .
.
Осуществив расчет по формуле (5) для всех полученных в эксперименте значений  , определим совокупность
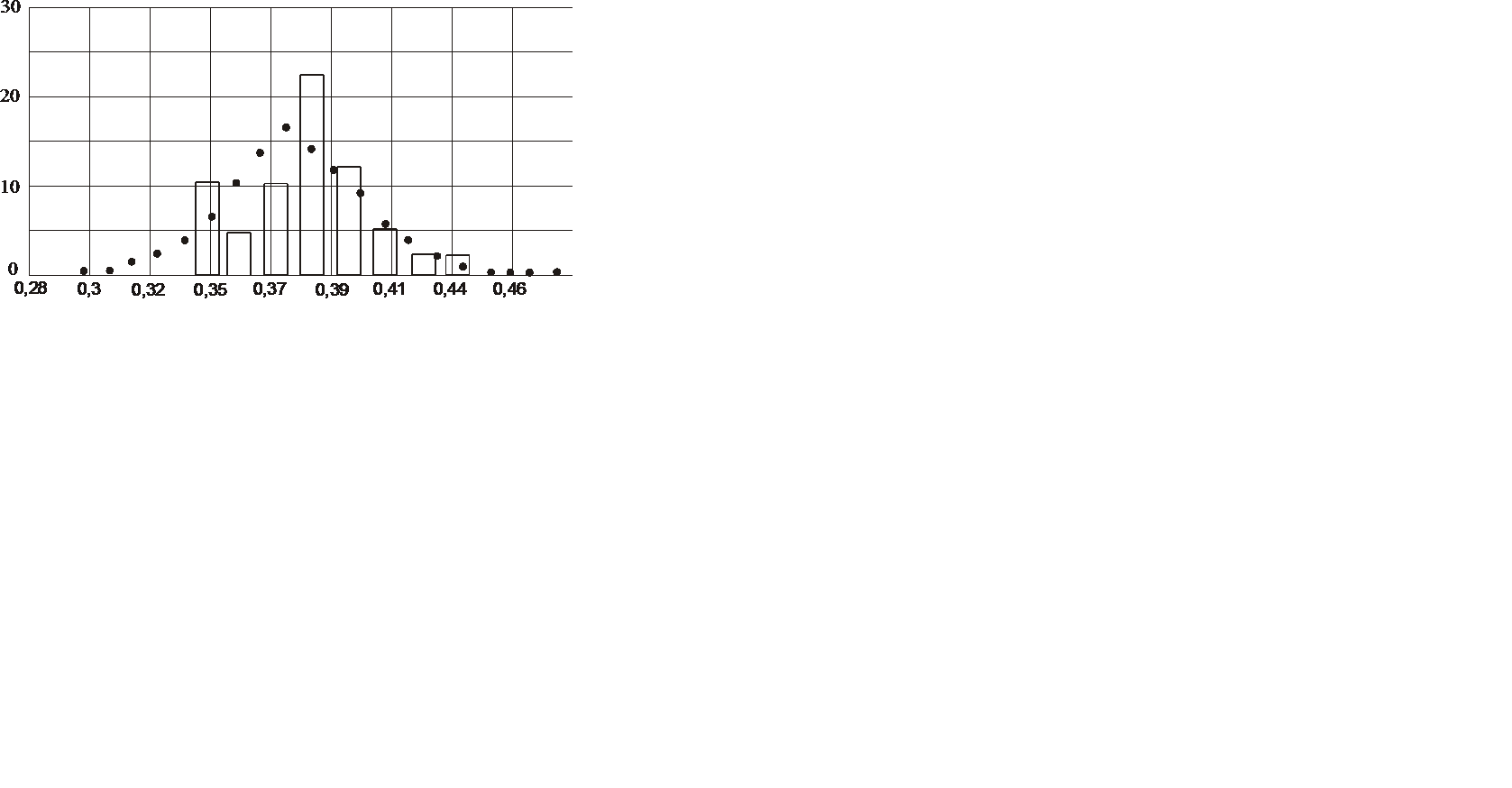
, определим совокупность  , которая является выборкой случайной величины Пg. Обработка конкретных данных ранее выполненных тарировочных испытаний ДДИТ [2] свидетельствует [3, 4], что с вероятностью 0,9 и выше случайная величина Пg подчиняется нормальному закону распределения. Гистограмма частот распределения величины Пg показана на рисунке 1.
, которая является выборкой случайной величины Пg. Обработка конкретных данных ранее выполненных тарировочных испытаний ДДИТ [2] свидетельствует [3, 4], что с вероятностью 0,9 и выше случайная величина Пg подчиняется нормальному закону распределения. Гистограмма частот распределения величины Пg показана на рисунке 1.
|
Рассчитаем на основе результатов работы [3] оценки параметров нормального распределения величины поврежденности датчика Пg, когда случайная выборка  объема ng извлечена из нормального распределения, усеченного снизу
объема ng извлечена из нормального распределения, усеченного снизу  и сверху
и сверху  . Следуя этой работе, для определения оценок максимального правдоподобия
. Следуя этой работе, для определения оценок максимального правдоподобия  и Sn ( математического ожидания и дисперсии случайной величины Пg) используются рекуррентные соотношения вида
и Sn ( математического ожидания и дисперсии случайной величины Пg) используются рекуррентные соотношения вида
| (6) |

где  и
и  - выборочные моменты, вычисляемые по зависимостям:
- выборочные моменты, вычисляемые по зависимостям:
 (7)
(7)
В выражениях (6) через j и Ф соответственно обозначены ордината и кумулятивная площадь под кривой стандартного нормального распределения, индекс "k" означает k-е приближение оценки максимального правдоподобия. Вычисления по формулам (6) осуществляют до тех пор, пока не будет достигнута необходимая точность (изменения Пg,k и Sn,k будут происходить в заданном знаке после запятой). В результате определяются оценки величин  и
и  . После чего максимальное Пgmax и минимальное Пgmin значения случайной величины Пg рассчитываются по следующим формулам:
. После чего максимальное Пgmax и минимальное Пgmin значения случайной величины Пg рассчитываются по следующим формулам:
 , (8)
, (8)
где ta,k - критерий Стьюдента при уровне значимости a и числе степеней свободы k = ng - 1.
В результате обработки по вышеизложенному алгоритму данных тарировочных испытаний (табл. 1 [2]) получены следующие значения величин, входящих в формулы (8):  = 0,376 и
= 0,376 и  0,027. После чего по выражениям (8) рассчитаны величины Пgmin = 0,3639 и Пgmax = 0,388 , при этом
0,027. После чего по выражениям (8) рассчитаны величины Пgmin = 0,3639 и Пgmax = 0,388 , при этом  .
.
Подставляя в зависимость (4) вместо Пg установленные по выражениям (8) величины Пgmin, Пgmax,получаем нижнюю и верхнюю границы доверительного интервала тарировочной зависимости:
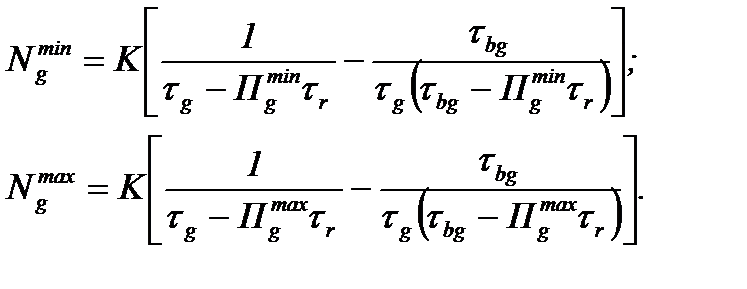 (9)
(9)
При  уравнение (4) описывает данные тарировочных испытаний ДДИТ при 50% вероятности.
уравнение (4) описывает данные тарировочных испытаний ДДИТ при 50% вероятности.
Результаты выполненных расчетов по формулам (9) отражены на рис. 2, где показаны экспериментальные точки  и границы 99% доверительного интервала.
и границы 99% доверительного интервала.
Ранее отмечалось, что на разброс показаний датчиков при их тарировании на образцах влияют механические свойства материала образцов, особенно проявляющиеся при их испытаниях на выносливость. Поскольку выше для предела выносливости уже получены статистические характеристики [1], учтем их в разработанной модели аппроксимации данных эксперимента. Принимая изложенное во внимание, окончательный вид уравнений для расчета границ доверительного интервала следующий:
 (10)
(10)

|
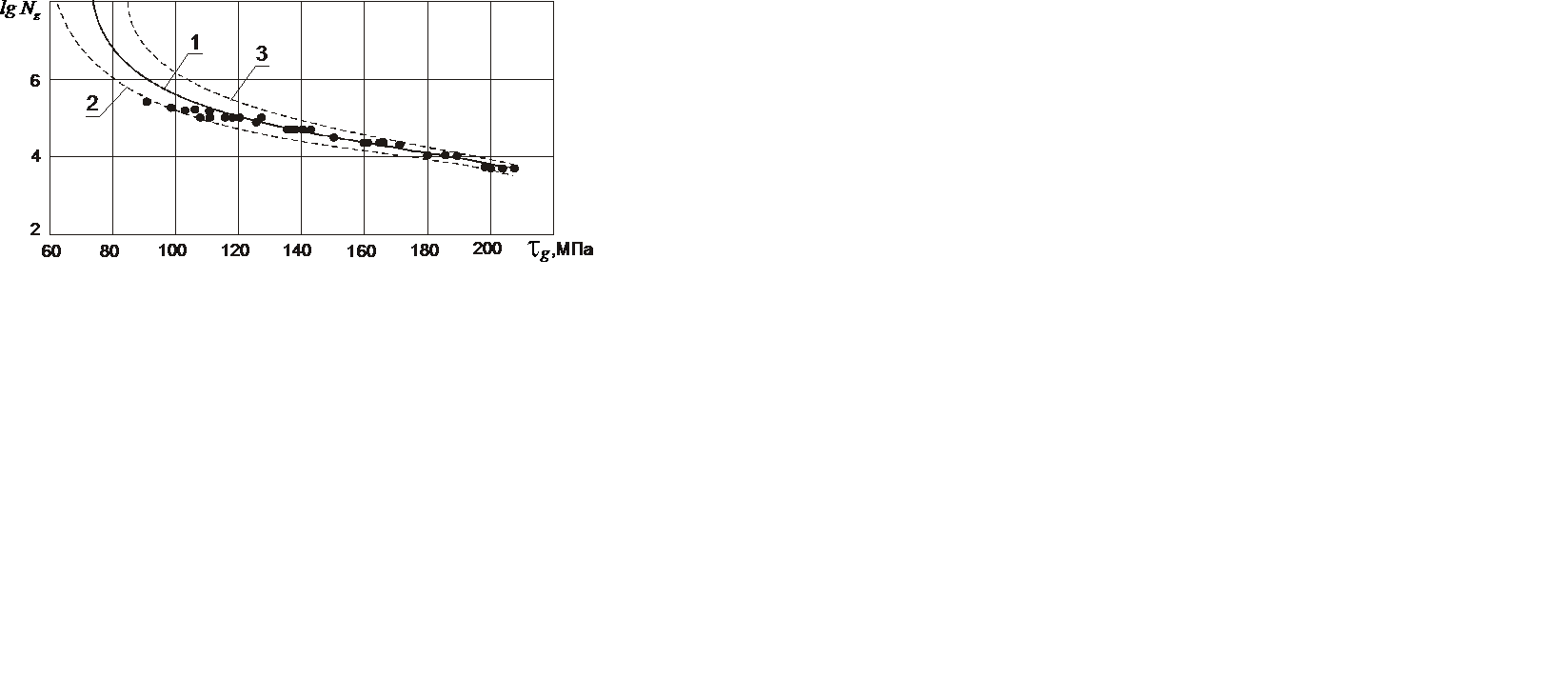
Расчеты по формулам (10) отражены на рис. 3, откуда следует, что качество аппроксимации по сравнению с рис. 4 [2] и 2 существенно выше.
|
Таким образом, обработка данных тарирования алюминиевых ДДИТ завершена.
Ñïèñîê ëèòåðàòóðû
1. В.Н. Сызранцев, С.Л. Голофаст, О.В. Богомолов, Ю.С. Иванова. Применение датчиков деформаций интегрального типа для оценки нагруженности валов и роторов. Известия вузов. Нефть и газ. – Тюмень. 2005. – №6. С.105-112.
2. Тарирование датчиков деформаций интегрального типа для оценки нагруженности валов и роторов. Известия вузов. Нефть и газ. – Тюмень. 2006. – № 1. С. 85-93.
3. Сызранцев В.Н., Голофаст С.Л. Измерение циклических деформаций и прогнозирование долговечности деталей по показаниям датчиков деформаций интегрального типа. - Новосибирск: Наука, Сибирская издательская фирма РАН, 2004. 206 с.
4. Сызранцев В.Н., Голофаст С.Л., Сызранцева К.В. Диагностика нагруженности и ресурса деталей трансмиссий и несущих систем машин по показаниям датчиков деформаций интегрального типа. - Новосибирск: Наука, Сибирская издательская фирма РАН, 2004. 188 с.
5. Коллинз Дж. Повреждение материалов в конструкции. Анализ, предсказание, предупреждение: Пер. с англ. - М.: Мир, 1984. 624 с.
6. Шенк Х. Теория инженерного эксперимента. Пер. с англ. – М.: Мир, 1972. 382 с.
(13) Тема 2009-2-4 С. Моделирование оценок запасов нефти.
Зиганшин А.Р. Использование модельных запасов нефти для выбора первоочередных поисковых объектов (на примере Тимано-Печорской НГП) // Известия высших учебных заведений. Нефть и газ. 2009. № 2. С. 4 – 7
УДК 550.834
Дата добавления: 2018-02-28; просмотров: 620; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
