Примеры задач для участников 7-9 классов
Задание 1.
1.1.Жесткий стержень скользит по ровной плоской поверхности. В некоторый момент времени скорость одного из его концов направлена перпендикулярно стержню. Под каким углом друг к другу направлены в этот момент скорости центра стержня и другого конца? Известно, что этот угол не равен нулю и что величина этих скоростей также отлична от нуля. Ответ запишите в градусах.
Подсказка 1: расстояние между любыми двумя точками жесткого стержня не изменяется при его движении.
Подсказка 2: из утверждения подсказки 1 следует, что проекции скоростей всех точек стержня на прямую, идущую вдоль стержня, равны.
Решение:
Расстояние между любыми двумя точками жесткого стержня не изменяется при его движении. Поэтому проекции скоростей всех точек стержня на прямую, идущую вдоль стержня, равны. Так как скорость одного из концов стержня имеет нулевую проекцию на эту прямую, то скорости всех точек также имеют нулевую проекцию. Значит, скорости другого конца и центра стержня направлены вдоль одной прямой. Так как угол между ними не равен нулю, то он равен 180°.
ОТВЕТ: 180.
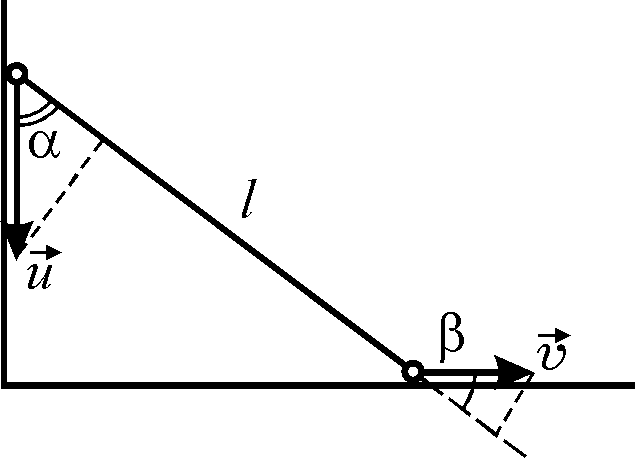
1.2.Один из узлов промышленного робота представляет собой два одинаковых маленьких шарика, соединенных легким жестким стержнем длиной  см. Один из шариков может свободно перемещаться по вертикальной направляющей, а другой − по горизонтальной. Первоначально стержень располагался вертикально. Из-за неосторожности, допущенной при сборке узла, нижний шарик сместился вправо на малое расстояние и система пришла в движение в плоскости рисунка. Найдите модуль скорости нижнего шарика
см. Один из шариков может свободно перемещаться по вертикальной направляющей, а другой − по горизонтальной. Первоначально стержень располагался вертикально. Из-за неосторожности, допущенной при сборке узла, нижний шарик сместился вправо на малое расстояние и система пришла в движение в плоскости рисунка. Найдите модуль скорости нижнего шарика  в момент времени, когда верхний шарик опустился до высоты
в момент времени, когда верхний шарик опустился до высоты 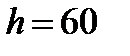 см над горизонтальной направляющей. Считайте, что при движении шарики не отрываются от направляющих, трением пренебрегите. Ускорение свободного падения примите равным
см над горизонтальной направляющей. Считайте, что при движении шарики не отрываются от направляющих, трением пренебрегите. Ускорение свободного падения примите равным  м/с2. Ответ запишите в виде десятичной дроби с одним знаком после запятой.
м/с2. Ответ запишите в виде десятичной дроби с одним знаком после запятой.
|
|
|
Подсказка 1: поскольку длина стержня постоянна, проекции скоростей шариков на направление стержня в каждый момент времени совпадают.
Подсказка 2: кинетическая энергия системы – сумма кинетических энергий шариков, потенциальная – энергия верхнего шарика в поле тяжести Земли.
 Подсказка 3: из закона сохранения механической энергии шариков следует равенство
Подсказка 3: из закона сохранения механической энергии шариков следует равенство  , где
, где  – угол между стержнем и вертикальной направляющей.
– угол между стержнем и вертикальной направляющей.
Решение:
Поскольку длина стержня постоянна, проекции скоростей шариков на направление стержня в каждый момент времени совпадают. Обозначив через 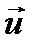 скорость верхнего шарика, имеем (см. рисунок):
скорость верхнего шарика, имеем (см. рисунок): 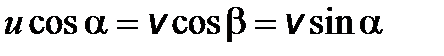 , откуда
, откуда  , где
, где 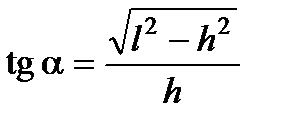 . Из закона сохранения механической энергии шариков следует равенство:
. Из закона сохранения механической энергии шариков следует равенство:  . Из записанных выражений получаем, что
. Из записанных выражений получаем, что  м/с.
м/с.
|
|
|
ОТВЕТ: 1,5.
Задание 2.
2.1. Найти расход воды (т.е. массу воды, вытекающую в единицу времени) для трубы сечением 20 см2, в которой вода движется со скоростью 4 м/с. Плотность воды считать равной 1 г/см3. Ответ дать в кг/с.
Подсказка 1: объем воды, протекающий за время  через трубу сечением
через трубу сечением  , равен
, равен 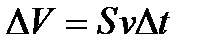 (где
(где  – скорость течения воды).
– скорость течения воды).
Подсказка 2: расход воды  , где
, где  – плотность воды.
– плотность воды.
Решение:
Объем воды, протекающий за время  через трубу сечением
через трубу сечением  , равен
, равен 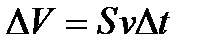 (где
(где  – скорость течения воды). Поэтому расход воды с плотностью
– скорость течения воды). Поэтому расход воды с плотностью  равен
равен  кг/с.
кг/с.
ОТВЕТ: 8.
2.2. Бензиновый двигатель модели потребляет 2 г бензина на 10 м пути при скорости движения 2 м/с. Его КПД равен 30%. Температура двигателя поддерживается постоянной за счет водяного охлаждения. Вода поступает в систему охлаждения двигателя из радиатора с температурой 25°С, а возвращается в радиатор с температурой 45°С. С какой скоростью циркулирует вода в системе охлаждения, если площадь сечения трубок в ней постоянна и равна 0,5 см2. Удельная теплота сгорания используемого бензина 45 МДж/кг, удельная теплоемкость воды 4,2 кДж/(кг·°С). Плотность воды считать равной 1 г/см3. Ответ дать в м/с.
|
|
|
Подсказка 1: расход воды в системе охлаждения  .
.
Подсказка 2: отводимое водой тепло равно разности количества тепла, выделившегося при сгорании топлива, и полезной работы двигателя.
Подсказка 3: следовательно, умножение расхода воды на ее удельную теплоемкость  и разность температур
и разность температур  на выходе и входе в систему охлаждения дает величину, равную 70% от теплоты сгорания бензина в единицу времени.
на выходе и входе в систему охлаждения дает величину, равную 70% от теплоты сгорания бензина в единицу времени.
Решение:
Отводимое водой тепло равно разности количества тепла, выделившегося при сгорании топлива, и полезной работы двигателя. Полезная работа двигателя за время  равна 30% от теплоты сгорания топлива
равна 30% от теплоты сгорания топлива  (
(  МДж/кг, а
МДж/кг, а 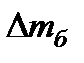 – масса сгоревшего бензина). Ясно, что
– масса сгоревшего бензина). Ясно, что  г соответствует
г соответствует  с. Расход воды в системе охлаждения
с. Расход воды в системе охлаждения  . Умножение расхода воды на ее удельную теплоемкость
. Умножение расхода воды на ее удельную теплоемкость  и разность температур
и разность температур  на выходе и входе в систему охлаждения дает величину, равную 70% от теплоты сгорания бензина в единицу времени. Таким образом,
на выходе и входе в систему охлаждения дает величину, равную 70% от теплоты сгорания бензина в единицу времени. Таким образом,
 м/с.
м/с.
ОТВЕТ: 5
Задание 3.
3.1. При работе светодиода напряжение на нем примерно постоянно и равно 7,5 В. Чему равно его сопротивление в рабочем режиме, в котором мощность излучаемого света составляет 9 Вт? КПД светодиода равно 80%. Ответ запишите в Омах.
|
|
|
Подсказка 1: Потребляемая светодиодом мощность равна 1,25×9 Вт.
Подсказка 2: Эта мощность равна  , где
, где  – напряжение на светодиоде, а
– напряжение на светодиоде, а  – его сопротивление.
– его сопротивление.
Решение:
Потребляемая светодиодом мощность равна 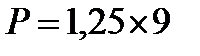 Вт. Эта мощность равна
Вт. Эта мощность равна  , где
, где  – напряжение на светодиоде, а
– напряжение на светодиоде, а  – его сопротивление. Поэтому
– его сопротивление. Поэтому  Ом.
Ом.
ОТВЕТ: 5.
3.2. Для световой панели с тремя светодиодами собрана схема, показанная на рисунке.
Резистор в схеме имеет сопротивлением  Ом. Для питания схемы используется источник постоянного напряжения. Оказалось, что при изменении положения движка реостата яркость свечения всех светодиодов совершенно не изменяется. При работе каждого светодиода напряжение на нем примерно постоянно и равно и двух светодиодов Ом. Для питания схемы используется источник постоянного напряжения. Оказалось, что при изменении положения движка реостата яркость свечения всех светодиодов совершенно не изменяется. При работе каждого светодиода напряжение на нем примерно постоянно и равно и двух светодиодов  В, а у третьего оно отличается от этого значения. КПД всех светодиодов равен 75%, а мощность излучаемого света у третьего В, а у третьего оно отличается от этого значения. КПД всех светодиодов равен 75%, а мощность излучаемого света у третьего
|
|
в два раза больше, чем у двух других. у двух из них номинальная мощность была равна 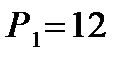 Вт, а у третьей –
Вт, а у третьей –  Вт. меняется. Найдите суммарную мощность излучения панели. Ответ запишите в Ваттах.
Вт. меняется. Найдите суммарную мощность излучения панели. Ответ запишите в Ваттах.
Подсказка 1: яркость свечения светодиодов не изменяется, если ток через реостат отсутствует при любом положении движка.
Подсказка 2: это возможно только в том случае, если напряжения на диодах в нижней части схемы равны друг другу, а напряжение на диоде в верхней части схемы равно напряжению на резисторе.
Подсказка 3: поскольку при одинаковом токе и одинаковом КПД мощность свечения светодиодов отличается в два раза, то и рабочие напряжения у них отличаются в два раза.
Решение:
Яркость свечения светодиодов не изменяется, если ток через реостат отсутствует при любом положении движка. Это возможно только в том случае, если напряжения на диодах в нижней части схемы равны друг другу, а напряжение на диоде в верхней части схемы равно напряжению на резисторе. Значит, два «нижних» светодиода одинаковы и напряжение на них равно  В. Поскольку при одинаковом токе и одинаковом КПД мощность свечения светодиодов отличается в два раза, то и рабочие напряжения у них отличаются в два раза. Следовательно, рабочее напряжение «верхнего» светодиода и напряжение на резисторе равны
В. Поскольку при одинаковом токе и одинаковом КПД мощность свечения светодиодов отличается в два раза, то и рабочие напряжения у них отличаются в два раза. Следовательно, рабочее напряжение «верхнего» светодиода и напряжение на резисторе равны 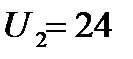 В. По закону Ома ток через резистор равен
В. По закону Ома ток через резистор равен  А, и такой же ток течет через все светодиоды. Значит, суммарная мощность, потребляемая тремя светодиодами, равна
А, и такой же ток течет через все светодиоды. Значит, суммарная мощность, потребляемая тремя светодиодами, равна 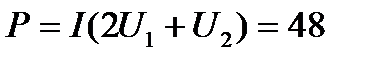 Вт, а мощность излучения
Вт, а мощность излучения  Вт.
Вт.
ОТВЕТ: 36.
При внимательном рассмотрении можно заметить, что многие физические идеи, нужные для решения тренировочных заданий, связаны с идеями, разобранными в заданиях отборочного этапа. И эта тенденция сохраняется и при переходе к заданиям финала!
ЗАДАНИЯ ТЕОРЕТИЧЕСКОГО ТУРА ЗАКЛЮЧИТЕЛЬНОГО ЭТАПА ПО ФИЗИКЕ:
Условия, решения и ответы
И 11 классы
БИЛЕТ № 01 (10-11 классы)
Задание 1:
Вопрос: На горизонтальной поверхности лежит доска, на которой покоится небольшой брусок массы  г. Коэффициент трения между доской и бруском равен
г. Коэффициент трения между доской и бруском равен 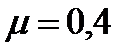 . Доску быстро сместили вдоль нее самой по поверхности на расстояние
. Доску быстро сместили вдоль нее самой по поверхности на расстояние  м. При этом брусок сдвинулся относительно поверхности на расстояние
м. При этом брусок сдвинулся относительно поверхности на расстояние  см. Какое количество тепла выделилось из-за трения между бруском и доской? Ускорение свободного падения
см. Какое количество тепла выделилось из-за трения между бруском и доской? Ускорение свободного падения  м/с2.
м/с2.
Ответ: Количество тепла равно модулю работы силы трения скольжения, которая равна  , а относительное смещение бруска и доски равно
, а относительное смещение бруска и доски равно  . Итак,
. Итак,  Дж.
Дж.
Задача: Модель бульдозера должна вытеснить за пределы поля небольшую коробку. Скорость
модели направлена перпендикулярно краю поля, а ковш повернут на угол  относительно этого края (см. рисунок). Начальное расстояние от коробки до края поля относительно этого края (см. рисунок). Начальное расстояние от коробки до края поля  м, коэффициент трения между ковшом и коробкой м, коэффициент трения между ковшом и коробкой  . Найдите координату . Найдите координату  точки, в которой коробка пройдет край. Во сколько раз отличаются количества теплоты, выделившиеся из-за трения между ковшом и коробкой и между коробкой и полом? Коэффициент трения коробки о пол точки, в которой коробка пройдет край. Во сколько раз отличаются количества теплоты, выделившиеся из-за трения между ковшом и коробкой и между коробкой и полом? Коэффициент трения коробки о пол  . .
|
|
Коробка движется поступательно и не отрывается от ковша. Скорость модели постоянна.
Решение: Коробка двигалась бы перпендикулярно краю поля, если бы не скользила по ковшу.
Но в этом случае также была бы направлена и равнодействующая сил трения о ковш и силы нормальной реакции ковша. Но тогда между этими силами выполнялось бы соотношение  , что невозможно, ибо , что невозможно, ибо  . Значит, коробка скользит по ковшу. Поэтому результирующая сила . Значит, коробка скользит по ковшу. Поэтому результирующая сила  направлена под углом направлена под углом
|
|
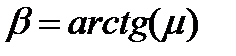 к силе
к силе  , то есть под углом
, то есть под углом  к перпендикуляру к краю поля. Значит,
к перпендикуляру к краю поля. Значит, 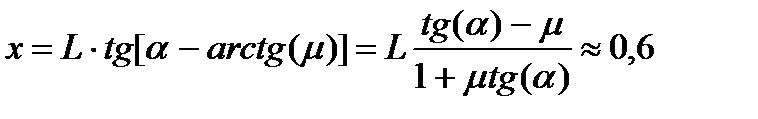 м. Так как скорость модели постоянна, то и скорость коробки почти на всем пути постоянна, и поэтому сила
м. Так как скорость модели постоянна, то и скорость коробки почти на всем пути постоянна, и поэтому сила  равна по величине силе трения коробки о пол
равна по величине силе трения коробки о пол  . Тогда
. Тогда 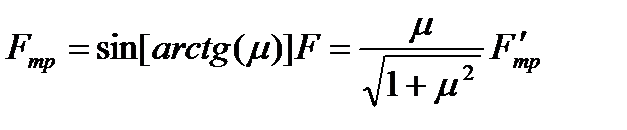 , и соотношение количеств теплоты, выделившиеся из-за трения между ковшом и коробкой и между коробкой и полом
, и соотношение количеств теплоты, выделившиеся из-за трения между ковшом и коробкой и между коробкой и полом  , где
, где  – величина проскальзывания коробки по ковшу, а и
– величина проскальзывания коробки по ковшу, а и  – путь коробки по полу. Из геометрии находим; что
– путь коробки по полу. Из геометрии находим; что  , а
, а  . Итак,
. Итак,  .
.
Ответ:  м,
м,  .
.
Задание 2:
Вопрос: На сколько процентов нужно изотермически уменьшить объем идеального газа, чтобы его давление возросло на 25%? А на 0,5% (ответ дайте с точностью до 0,1%)?
Ответ: Согласно закону Бойля-Мариотта, в изотермическом процессе  . Поэтому, если
. Поэтому, если  , то
, то  , то есть для увеличения давления на 25% нужно уменьшить объем на 20%. Аналогично для
, то есть для увеличения давления на 25% нужно уменьшить объем на 20%. Аналогично для 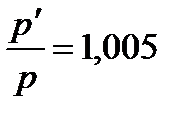 получается
получается  , то есть во втором случае уменьшить объем нужно примерно на 0,5%. Можно сделать вывод: при малых изменениях величины относительных изменений совпадают с точностью до поправок большего порядка малости.
, то есть во втором случае уменьшить объем нужно примерно на 0,5%. Можно сделать вывод: при малых изменениях величины относительных изменений совпадают с точностью до поправок большего порядка малости.
Задача: В конструкции специализированного робота используется акселерометр (датчик
| ускорения) следующей конструкции: в гладкой герметичной горизонтальной трубке, заполненной газом, находится небольшой поршень. В отсутствие ускорения поршень располагается точно посередине трубки. |
|
При появлении продольного ускорения поршень смещается. На испытаниях робот двигался с ускорением  м/с2, а температура газа равнялась
м/с2, а температура газа равнялась  , и при этом смещение поршня составило
, и при этом смещение поршня составило  мм. В один из моментов работы робота смещение поршня равнялось
мм. В один из моментов работы робота смещение поршня равнялось  мм при температуре газа
мм при температуре газа  . С каким продольным ускорением двигался робот? Ответ нужно получить с ошибкой менее 2%.
. С каким продольным ускорением двигался робот? Ответ нужно получить с ошибкой менее 2%.
Решение: Поскольку в отсутствие ускорения поршень располагается точно посередине трубки, то в трубке по разные стороны от поршня находится одинаковое количество газа  . Запишем уравнение Менделеева-Клапейрона для газа в каждой из частей трубки, в которой поршень смещен от середины на
. Запишем уравнение Менделеева-Клапейрона для газа в каждой из частей трубки, в которой поршень смещен от середины на 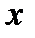 при температуре
при температуре  :
:  (здесь
(здесь  – площадь поперечного сечения трубки). Дополним их уравнением движения поршня массой
– площадь поперечного сечения трубки). Дополним их уравнением движения поршня массой  , движущегося вместе с трубкой с ускорением
, движущегося вместе с трубкой с ускорением  :
:  . Выразив силы давления из первых двух соотношений и подставив их в третье, получим связь ускорения и смещения:
. Выразив силы давления из первых двух соотношений и подставив их в третье, получим связь ускорения и смещения:
 .
.
При указанных в условиях величинах ускорений и температурах, близких к нормальной, смешения небольшого по массе поршня должны быть малы по сравнению с длиной трубки (  ). Поэтому в знаменателе можно пренебречь
). Поэтому в знаменателе можно пренебречь  по сравнению с
по сравнению с 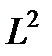 , и тогда
, и тогда  . Например, если давление в трубке близко к нормальному атмосферному, а масса поршня равна 100 г при площади 1 см2 (то есть он весьма тяжелый), то для создания ускорения в 1 м/с2 достаточно, чтобы разность давлений составляла 1% от равновесного давления. Того же порядка должна быть и относительная разность объемов, тогда
. Например, если давление в трубке близко к нормальному атмосферному, а масса поршня равна 100 г при площади 1 см2 (то есть он весьма тяжелый), то для создания ускорения в 1 м/с2 достаточно, чтобы разность давлений составляла 1% от равновесного давления. Того же порядка должна быть и относительная разность объемов, тогда 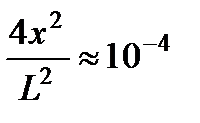 ! Значит, точность полученной формулы при разумных значениях параметров акселерометра значительно лучше требуемой. Таким образом, для разных значений температуры и ускорения
! Значит, точность полученной формулы при разумных значениях параметров акселерометра значительно лучше требуемой. Таким образом, для разных значений температуры и ускорения  м/с2. В вычислениях округление производим с учетом требуемой точности.
м/с2. В вычислениях округление производим с учетом требуемой точности.
Ответ:  м/с2.
м/с2.
Задание 3:
Вопрос: Электродвигатель, работающий от источника постоянной ЭДС, поднимает по очереди два разных груза. Сила тяги двигателя пропорциональна силе тока, текущего в обмотке. Для первого груза эта сила тока меньше, чем для второго. Какой из грузов поднимается с большей установившейся скоростью? Ответ объяснить.
Ответ: Работа сторонних сил источника с ЭДС  идет на механическую работу двигателя, перемещающего груз силой
идет на механическую работу двигателя, перемещающего груз силой 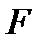 со скоростью
со скоростью  , и на компенсацию тепловых потерь на сопротивлении
, и на компенсацию тепловых потерь на сопротивлении  , то есть
, то есть  . Если
. Если  , то
, то  , то есть установившаяся скорость больше при меньшем токе. Значит, большая скорость у первого груза.
, то есть установившаяся скорость больше при меньшем токе. Значит, большая скорость у первого груза.
Задача: Двигатель робота работает от аккумулятора с ЭДС  В. Известно, что сила, с которой двигатель натягивает наматывающийся на вал прочный легкий трос, прямо пропорциональна силе тока, текущего в обмотке. Когда закрепленный робот поднимает вверх с помощью этого троса груз массой
В. Известно, что сила, с которой двигатель натягивает наматывающийся на вал прочный легкий трос, прямо пропорциональна силе тока, текущего в обмотке. Когда закрепленный робот поднимает вверх с помощью этого троса груз массой  кг, ток в обмотке равен
кг, ток в обмотке равен  А при установившейся скорости подъема
А при установившейся скорости подъема  м/с. С какой установившейся скоростью закрепленный робот будет подтягивать этим же тросом тот же груз по горизонтальной поверхности? Коэффициент трения между грузом и поверхностью
м/с. С какой установившейся скоростью закрепленный робот будет подтягивать этим же тросом тот же груз по горизонтальной поверхности? Коэффициент трения между грузом и поверхностью  .
.
Решение: При установившейся скорости подъема ускорение груза равно нулю, то есть сила тяги двигателя уравновешивает вес груза. Значит, уравнение энергетического баланса имеет вид  , причем, поскольку
, причем, поскольку  , то
, то 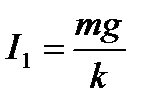 . Во тором случае при установившемся движении сила тяги уравновешивает силу трения скольжения, то есть
. Во тором случае при установившемся движении сила тяги уравновешивает силу трения скольжения, то есть 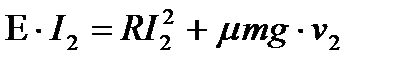 и
и  . Исключая из уравнений энергетического баланса сопротивление контура обмотки, получаем:
. Исключая из уравнений энергетического баланса сопротивление контура обмотки, получаем:  . Таким образом,
. Таким образом, 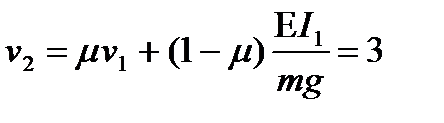 м/с.
м/с.
Ответ:  м/с.
м/с.
Задание 4:
Вопрос: При каких условиях можно наблюдать явление полного внутреннего отражения?
Ответ: Полное внутреннее отражение наблюдается в ситуациях, когда закон Снелла выдает для синуса угла преломления невозможное (≥ 1) значение. Такое возможно, если луч выходит из оптически более плотной среды с показателем преломления  в оптически менее плотную – с
в оптически менее плотную – с  , и угол падения превышает по величине «угол полного внутреннего отражения»
, и угол падения превышает по величине «угол полного внутреннего отражения»  .
.
Задача: В оптической системе робота используется так называемый планарный световод,
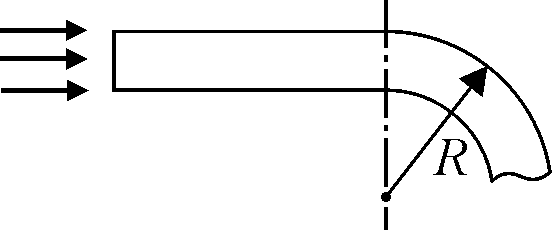
представляющий собой плоскопараллельную пластинку толщиной 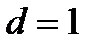 мм, изготовленную из прозрачной пластмассы с показателем преломления мм, изготовленную из прозрачной пластмассы с показателем преломления  . Изгибая пластинку, ей придают форму, изображенную на рисунке. Перпендикулярно торцу пластинки падает в . Изгибая пластинку, ей придают форму, изображенную на рисунке. Перпендикулярно торцу пластинки падает в
| 
|
плоскости рисунка параллельный пучок света. Найдите минимально допустимый радиус кривизны  изгиба пластинки, при котором свет не будет выходить из пластинки наружу через ее боковую поверхность. Радиус кривизны определяйте по внешней (по отношению к направлению изгиба) поверхности пластинки.
изгиба пластинки, при котором свет не будет выходить из пластинки наружу через ее боковую поверхность. Радиус кривизны определяйте по внешней (по отношению к направлению изгиба) поверхности пластинки.
Решение:Рассмотрим ход светового луча, распространяющегося вплотную к внутренней поверхности плоской части пластинки (см. рисунок). Легко видеть, что из всех лучей,

| попавших внутрь пластинки через ее торец, этот луч имеет наименьший угол падения  на искривленную поверхность пластинки. Рассматриваемый луч не выйдет наружу, если он испытает на искривленной поверхности полное отражение, условие которого имеет вид: на искривленную поверхность пластинки. Рассматриваемый луч не выйдет наружу, если он испытает на искривленной поверхности полное отражение, условие которого имеет вид:  . Ясно, при выполнении этого условия все остальные лучи, образующие пучок, также не выйдут . Ясно, при выполнении этого условия все остальные лучи, образующие пучок, также не выйдут
|
из пластинки через ее искривленную поверхность. На рисунке видно, что  . Из записанных соотношений находим, что
. Из записанных соотношений находим, что 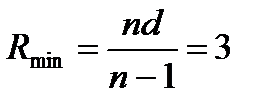 мм.
мм.
Ответ:  мм.
мм.
БИЛЕТ № 05 (7-9 классы)
Задание 1:
Вопрос: Жесткий стержень движется в плоскости. В некоторый момент времени скорость одного из его концов равна 0,5 м/с и направлена вдоль стержня. В тот же момент времени скорость другого конца стержня равна 1 м/с. Под каким углом к стержню направлена эта скорость? Ответ объяснить.
Ответ: Так как длина «жесткого» стержня не должна изменяться, то проекции скоростей его точек на стержень должны быть одинаковы и поэтому равны 0,5 м/с. Такой должна быть и проекция скорости «другого конца», то есть проекция (катет прямоугольного треугольника, образованного вектором скорости, его проекцией и перпендикуляром к стержню) должна равняться половине самой скорости (гипотенузы). Значит, прилежащий угол для этого катета – угол между скоростью и стержнем – равен 60°.
Задача: Вам необходимо изучить движение следующего механического устройства: три
одинаковых массивных шарика прикреплены к концам и середине легкого жесткого стержня. Длина стержня  м. Крайние шарики могут без трения скользить по вертикальной и горизонтальной направляющим (см. рисунок). Средний шарик шарнирно соединен с легким жестким стержнем вдвое меньшей длины. Второй конец этого стержня прикреплен (также с помощью шарнира) к перекрестью направляющих. Изначально стержень располагают вдоль вертикальной направляющей и отпускают без начальной скорости. Трения нигде нет, крайние шарики не м. Крайние шарики могут без трения скользить по вертикальной и горизонтальной направляющим (см. рисунок). Средний шарик шарнирно соединен с легким жестким стержнем вдвое меньшей длины. Второй конец этого стержня прикреплен (также с помощью шарнира) к перекрестью направляющих. Изначально стержень располагают вдоль вертикальной направляющей и отпускают без начальной скорости. Трения нигде нет, крайние шарики не
|
|
отрываются от направляющих и не застревают в них. По какой траектории будет двигаться средний шарик? Куда будет направлена его скорость в тот момент, когда длинный стержень будет проходить положение, в котором он составляет 45˚ с горизонтом? Найдите величину этой скорости. Ускорение свободного падения 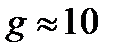 м/с2.
м/с2.
Решение: Расстояние между средним шариком и перекрестьем направляющих все время остается постоянным (равным половине  ). Поэтому ясно, что средний шарик движется по окружности радиуса
). Поэтому ясно, что средний шарик движется по окружности радиуса  . Его скорость в любой момент времени направлена по касательной к этой окружности, и в момент, когда длинный стержень будет проходить положение, в котором
. Его скорость в любой момент времени направлена по касательной к этой окружности, и в момент, когда длинный стержень будет проходить положение, в котором
он составляет 45˚ с горизонтом, эта скорость будет направлена вдоль стержня. Пусть ее величина в этот момент равна  . Так как длина стержня не должна изменяться, то проекции скоростей шариков на стержень должны быть одинаковы, поэтому скорости крайних шариков в этот момент одинаковы и равны . Так как длина стержня не должна изменяться, то проекции скоростей шариков на стержень должны быть одинаковы, поэтому скорости крайних шариков в этот момент одинаковы и равны 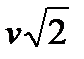 . Следовательно, кинетическая энергия системы в этот момент времени . Следовательно, кинетическая энергия системы в этот момент времени 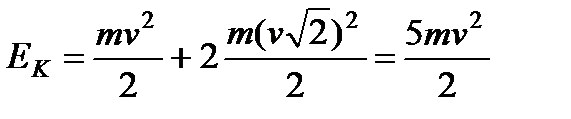 . Так как эта энергия появилась из-за убыли потенциальной энергии верхнего и . Так как эта энергия появилась из-за убыли потенциальной энергии верхнего и
|
|
среднего шариков в поле тяжести Земли  , то
, то  , и из этого соотношения находим, что
, и из этого соотношения находим, что  м/с.
м/с.
Ответ: средний шарик движется по окружности радиуса  , в указанный момент времени его скорость направлена вниз вдоль длинного стержня, а ее величина
, в указанный момент времени его скорость направлена вниз вдоль длинного стержня, а ее величина  м/с.
м/с.
Задание 2:
Вопрос: Двигатель с КПД 50% работает от аккумулятора, напряжение на клеммах которого неизменно и равно 12 В. За время полной разрядки аккумулятора двигатель совершил работу 324 Дж. Какова «емкость» аккумулятора (так называют величину заряда, который перемещает аккумулятор до полной разрядки)? Выразите ответ в миллиампер-часах (мА·ч).
Ответ: Потраченная аккумулятором энергия в два раза больше полезной работы, то есть 648 Дж. Но она равна произведению напряжения на перемещенный заряд. Поэтому «емкость» аккумулятора равна  (Кл). Так как 1 ч = 3600 с, то 1мА·ч=0,001А·3600с=3,6 Кл, то есть 54 Кл = 15 мА·ч.
(Кл). Так как 1 ч = 3600 с, то 1мА·ч=0,001А·3600с=3,6 Кл, то есть 54 Кл = 15 мА·ч.
Задача: Двигатель робота работает от аккумулятора, создающего неизменное напряжение  В. Емкость аккумулятора
В. Емкость аккумулятора  мА·ч. Во время работы, в ходе которой аккумулятор полностью разрядился за время
мА·ч. Во время работы, в ходе которой аккумулятор полностью разрядился за время  ч, у двигателя поддерживалась постоянная температура за счет водяного охлаждения. Вода циркулирует в системе охлаждения по трубкам постоянного сечения
ч, у двигателя поддерживалась постоянная температура за счет водяного охлаждения. Вода циркулирует в системе охлаждения по трубкам постоянного сечения  см2 со скоростью
см2 со скоростью  м/с. Она поступает в систему охлаждения двигателя из радиатора с температурой 25°С, а возвращается в радиатор с температурой 28°С. Удельная теплоемкость воды
м/с. Она поступает в систему охлаждения двигателя из радиатора с температурой 25°С, а возвращается в радиатор с температурой 28°С. Удельная теплоемкость воды  Дж/(кг·°С), плотность воды считать равной
Дж/(кг·°С), плотность воды считать равной  кг/м3. Считая, что все потери связаны с выделяющимся теплом, найти КПД двигателя.
кг/м3. Считая, что все потери связаны с выделяющимся теплом, найти КПД двигателя.
Решение: Ток через обмотку двигателя  А. Поэтому мощность затрат аккумулятора
А. Поэтому мощность затрат аккумулятора  Вт. Объем воды, протекающий за время
Вт. Объем воды, протекающий за время  через трубу сечением
через трубу сечением  , равен
, равен 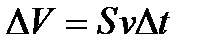 (где
(где  – скорость течения воды). Поэтому расход воды с плотностью
– скорость течения воды). Поэтому расход воды с плотностью  равен
равен  кг/с. Умножение расхода воды на ее удельную теплоемкость
кг/с. Умножение расхода воды на ее удельную теплоемкость  и разность температур
и разность температур  на выходе и входе в систему охлаждения дает мощность тепловых потерь
на выходе и входе в систему охлаждения дает мощность тепловых потерь  Вт. Полезная мощность равна разности мощности затрат и мощности тепловых потерь. Значит, КПД двигателя
Вт. Полезная мощность равна разности мощности затрат и мощности тепловых потерь. Значит, КПД двигателя  .
.
Ответ: 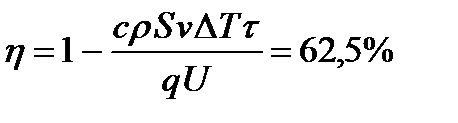 .
.
Задание 3:
Вопрос: Когда светодиод находится в «открытом» состоянии, напряжение на нем практически не зависит от протекающего тока. Пусть это напряжение равно 8 В. Какова величина силы тока, протекающего через светодиод, если мощность излучаемого света составляет 12 Вт? КПД светодиода равно 75%.
Ответ: Мощность, потребляемая светодиодом, равна 12Вт:0,75 = 16 Вт. Сила тока через светодиод 16Вт:8В = 2А.
Задача: Цепь питания светодиода собрана по схеме, показанной на рисунке. Яркость его свечения регулируется с помощью реостата. При сопротивлении реостата  Ом мощность излучения светодиода равна Ом мощность излучения светодиода равна 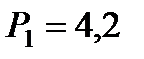 Вт, при Вт, при 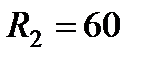 Ом – Ом –  Вт. Какой будет мощность излучения светодиода при максимальном сопротивлении реостата, равном Вт. Какой будет мощность излучения светодиода при максимальном сопротивлении реостата, равном  Ом? Можно считать, что КПД светодиода одинаков при любой мощности и напряжение на нем не зависит от протекающего тока. Ом? Можно считать, что КПД светодиода одинаков при любой мощности и напряжение на нем не зависит от протекающего тока.
|
|
Решение: Так как светодиод излучает, то он находится в открытом состоянии – напряжение, создаваемое источником, больше порогового напряжения светодиода. На светодиоде падает постоянное напряжение 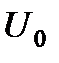 . Тогда по закону Ома ток через реостат с сопротивлением
. Тогда по закону Ома ток через реостат с сопротивлением  равен
равен  . С другой стороны, ток через резистор равен
. С другой стороны, ток через резистор равен  . Ток через светодиод
. Ток через светодиод  , поэтому
, поэтому  . Тогда мощность излучения светодиода
. Тогда мощность излучения светодиода  (в этой формуле
(в этой формуле  – КПД светодиода). Нетрудно заметить, что эта формула описывает линейную зависимость мощности от
– КПД светодиода). Нетрудно заметить, что эта формула описывает линейную зависимость мощности от  . Заметив, что
. Заметив, что  , понимаем, что
, понимаем, что  . Значит,
. Значит,  Вт.
Вт.
Ответ:  Вт.
Вт.
Задание 4:
Вопрос: Фотодатчик направлен на лампочку, и при расстоянии между ним и лампочкой в 50 см ток фотодатчика равен 72 мА. При каком расстоянии между фотодатчиком и лампочкой ток фотодатчика будет равен 8 мА? Лампочка светит одинаково во всех направлениях. Ток фотодатчика пропорционален мощности света, попадающего на фотодатчик. Влиянием среды (воздуха) на излучение лампы пренебречь.
Ответ: Площадь сферы пропорциональна квадрату радиуса. Энергия излучения лампочки равномерно распределяется по окружающей ее сфере, поэтому мощность света, попадающего на фотодатчик, обратно пропорциональна квадрату расстояния до нее до фотодатчика. Следовательно,  м.
м.
Задача: Робот находится на площадке в форме квадрата со стороной  м. В трех вершинах квадрата расположены лампы разных цветов, а робот снабжен тремя фотодатчиками, настроенными на эти же цвета (см. рисунок). Датчики настроены так, что при нахождении робота на расстоянии
м. В трех вершинах квадрата расположены лампы разных цветов, а робот снабжен тремя фотодатчиками, настроенными на эти же цвета (см. рисунок). Датчики настроены так, что при нахождении робота на расстоянии  м от любой из ламп ток соответствующего датчика равен
м от любой из ламп ток соответствующего датчика равен
 мА. По току трех датчиков в текущем положении программа робота определяет его положение на поле и направляет робота по кратчайшему пути в угол поля А со скоростью мА. По току трех датчиков в текущем положении программа робота определяет его положение на поле и направляет робота по кратчайшему пути в угол поля А со скоростью  м/с. За какое время робот достигнет А из положения, в котором токи датчиков равны м/с. За какое время робот достигнет А из положения, в котором токи датчиков равны  мА, мА,  мА и мА и  мА? мА?
|
|
Решение: Квадрат расстояния от каждой из ламп до робота обратно пропорционален току соответствующего датчика, то есть  ,
,  и
и 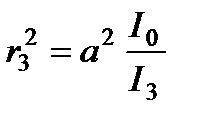 . С другой стороны, эти квадраты расстояний можно с помощью теоремы Пифагора выразить через
. С другой стороны, эти квадраты расстояний можно с помощью теоремы Пифагора выразить через
декартовы координаты робота относительно угла А. Если ось  направить от угла А к третьей лампочке, а ось направить от угла А к третьей лампочке, а ось  – к первой, совместив начало координат с углом А, то квадрат расстояния от первой лампы до робота – к первой, совместив начало координат с углом А, то квадрат расстояния от первой лампы до робота  . Аналогично . Аналогично  и также и также  . Из этих уравнений выражаем: . Из этих уравнений выражаем:
|
|
 .
.
Значит, робот находится от угла А на расстоянии  м. Время достижения этого угла площадки
м. Время достижения этого угла площадки  с.
с.
Ответ: за время  с.
с.
Внимательное изучение материалов заданий отчетливо демонстрирует, что они являются продолжением той «образовательной линии», которая берет свое начало от заданий отборочного этапа и проходила через задания, разбираемые на подготовительных занятиях.
Теперь разберем, как подводятся итоги заключительного этапа олимпиады «Робофест». В 2016/17 учебном году использовались следующие критерии определения победителей и призеров:
Для учащихся 10-11 классов:
ПОБЕДИТЕЛЬ (диплом I степени) ─ от 72 баллов включительно и выше;
ПРИЗЕР (диплом II степени) ─ от 66 баллов включительно до 71 балла включительно;
ПРИЗЕР (диплом III степени) ─ от 62 баллов включительно до 65 баллов включительно.
Для учащихся 7-9 классов:
ПОСТАНОВИЛИ:
Установить следующие критерии для определения победителей и призеров заключительного этапа олимпиады школьников «Робофест» по ФИЗИКЕ среди учащихся 7-9 классов:
ПОБЕДИТЕЛЬ (диплом I степени) ─ от 75 баллов включительно и выше;
ПРИЗЕР (диплом II степени) ─ от 58 баллов включительно до 74 баллов включительно; ПРИЗЕР (диплом III степени) ─ от 53 баллов включительно до 57 баллов включительно.
Итак, всякий из участников олимпиады, умеющий учиться и имеющий достаточно мотивации для серьезной работы – начиная от отборочного этапа и до финала, может стать победителем или призером олимпиады «Робофест». Поэтому – дерзайте!
Желаем успеха всем участникам Фестиваля «РобоФест» и олимпиады «Робофест»!
Дата добавления: 2018-02-28; просмотров: 327; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
