Элементарных функций

1) f(x)=e^x, f⁽ⁿ⁾(x)= e^x, f⁽ⁿ⁾(0)=1 "nÎN,

.

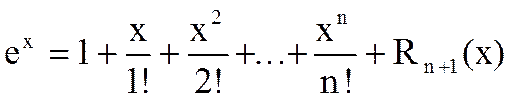Остаточный член в форме Лагранжа равен

.

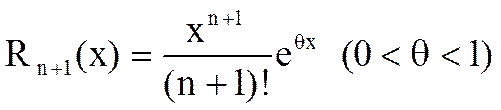На любом сегменте [-r, r] (r>0) в силу того, что ,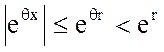

получим следующую оценку остаточного члена:

.

 

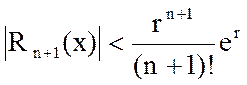2) f(x)=sinx. Поскольку 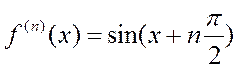(доказывается методом математической индукции),

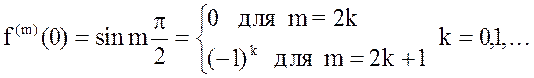(1)

 

Формула Маклорена имеет вид:

.

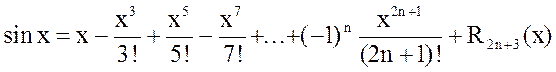Мы записали R_2n+3(x), а не R_2n+2(x), т.к. все члены разложения с четными номерами в силу (1) равны нулю.

.

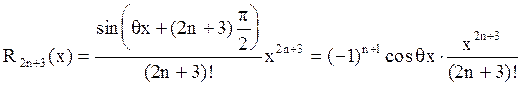На любом сегменте [-r, r] (r>0) .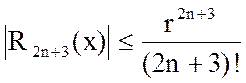

 

3) f(x)=cosx. Поскольку ,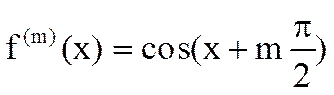

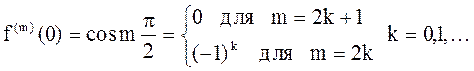(2)

 

Формула Маклорена имеет вид:

.

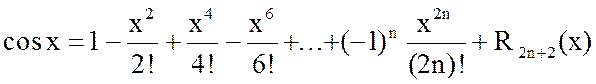Мы записали R_2n+2(x), а не R_2n+1(x), т.к. следующий за последним выписанным слагаемым член многочлена Тейлора в силу (2) равен нулю.

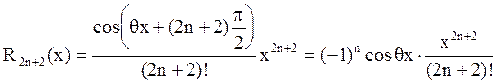
На любом сегменте [-r, r] .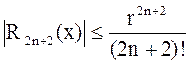

 

4) f(x)=ln(1+x)

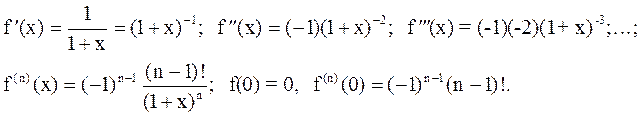
Формула Маклорена имеет вид:

.

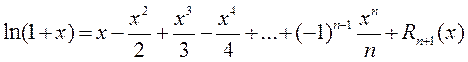Остаточный член запишем в форме Лагранжа

 

 

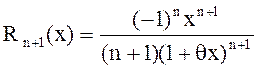
5) f(x)=(1+x)^a, где a - вещественное число

 

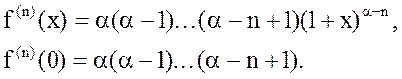
Формула Маклорена имеет вид:

,

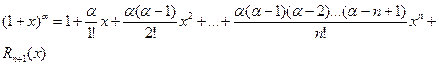где остаточный член в форме Лагранжа равен

.

 

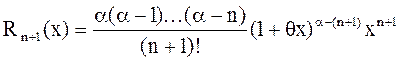В частном случае, когда 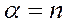- целое число, R_n+1(x)=0 и мы получим формулу бинома Ньютона

 

 

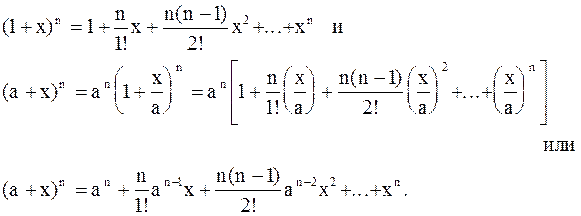
Итак, общий случай бинома Ньютона является частным случаем формулы Маклорена.

1.5.14.8.3. Приложения формулы Маклорена Приближенное

Вычисление числа е

 

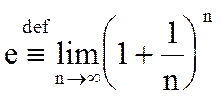. Ранее были установлены оценки 2 £е<3. Положим в формуле Маклорена для e^x, х=1 и r=1, получим

 

,

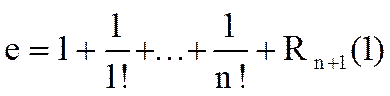где

.

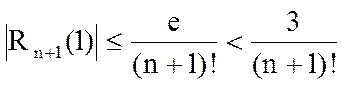Выбирая номер n достаточно большим, получим приближенное значение e с любой наперед заданной точностью.

 

---

Дата добавления: 2015-12-21; просмотров: 13; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!