Оценка остаточного члена в форме Лагранжа.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности U точки х=0 и существует М>0 такое, что 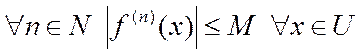, тогда

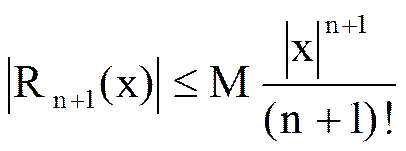Действительно,

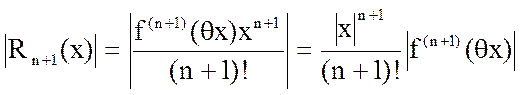Здесь (0<q<1), xÎUÞ qxÎUÞ ,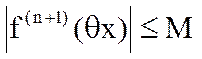

поэтому

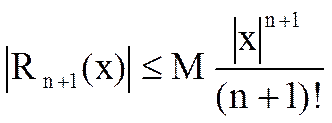. (1)

Замечание 1. 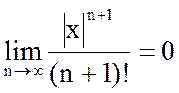при любом фиксированном x.

Докажем это. Положим

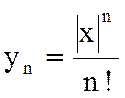, тогда .

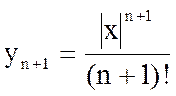Так как х фиксированно,

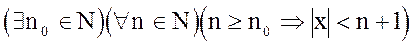Пусть n³n₀, тогда

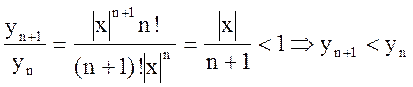т.е. начиная с номера n₀ последовательность 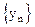является убывающей. Так как, кроме того, эта последовательность ограничена снизу (например, числом нуль), то по теореме п.2.7. она имеет предел y.

Для нахождения предела заметим, что

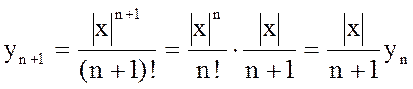Переходя к пределу при n®¥, получим y=0×y, т.е. y=0.

Таким образом, 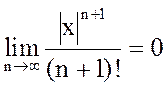(2)

Замечание 2. Из условий (1) и (2) следует. что, выбирая достаточно большой номер n, мы можем сделать R_n+1(x) как угодно малым. Таким образом, если заменить значение f(x) приближенным, равным

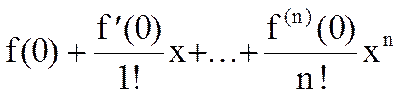то ошибка R_n+1(x) по абсолютной величине может быть сделана сколь угодно малой, если только в формуле Маклорена взято достаточно большое число членов.

Дата добавления: 2015-12-21; просмотров: 14; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!