Формула Тейлора с остаточным членом в форме Лагранжа
Теорема. (Тейлора). Пусть функция f(x) имеет в некоторой окрестности точки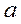 
производную порядка n+1 (где n - любой фиксированный номер). Пусть х - любое значение аргумента из указанной окрестности. Тогда между точками 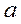и х найдется точка x такая, что справедлива следующая формула:
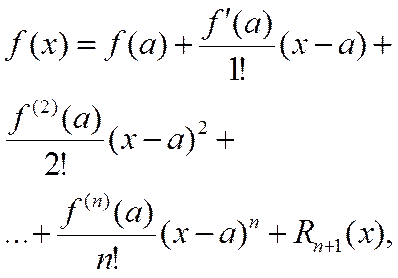где
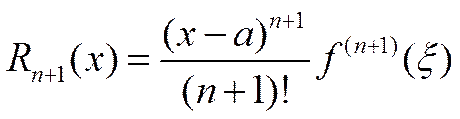-остаточный член в форме Лагранжа.
Замечание.
Точка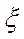 
зависит от n и x
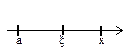,где a<x<x,
(x<x<a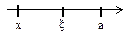 
).
Очевидно, найдется такое число q (q зависит от x, n): 0<q<1, что
x-a=q(x-a). Отсюда x=a+q(x-a), и
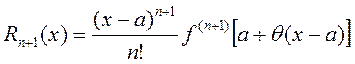- остаточный член в форме Лагранжа.
Сформулируем без доказательства следующую теорему.
Теорема. Пусть функция f(x) имеет производные до порядка (n-1) в некоторой окрестности точки а и производную порядка n в самой точке а, тогда справедливо равенство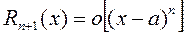 
(бесконечно малая при х®а более высокого порядка малости, чем 
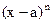). Последнее выражение есть остаточный член в форме Пеано.
Замечание. Запишем формулу Тейлора в несколько ином виде:
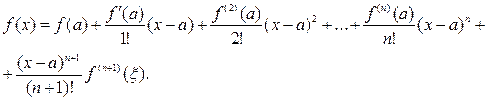
Пусть а=х0, х-а=Dх. Остаточный член запишем в форме Лагранжа,
тогда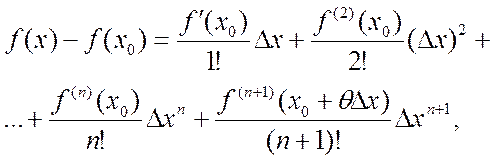 
где 0<q<1. При n=0 приходим к формуле Лагранжа:
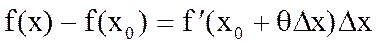. Таким образом, формула Тейлора является обобщением формулы Лагранжа.
Формула Маклорена
Формулой Маклорена называют формулу Тейлора с центром в точке а=0, т.е. формула Маклорена дает представление функции в окрестности точки х=0. Формула Маклорена с остаточным членом в форме Лагранжа, Коши и Пеано имеет вид:
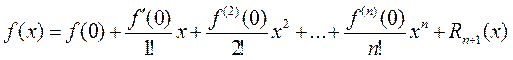где
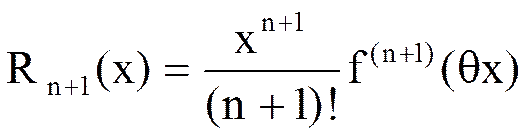(0<q<1) (остаточный член, записанный в форме Лагранжа).
|
|
|
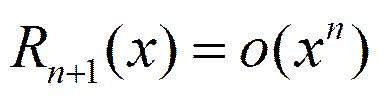(остаточный член, записанный в форме Пеано)
Дата добавления: 2015-12-21; просмотров: 15; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!