Метод Остроградского.
Пусть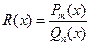 
- правильная рациональная дробь вещественного аргумента (
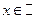), у которой многочлены 
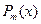и 
и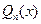меют вещественные коэффициенты. Представим
,
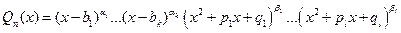где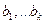 
- различные вещественные корни многочлена , 
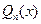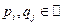(i,j=1,…,l), трёхчлен 
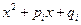(i=1,…,l) имеет комплексно сопряжённые корни (различные при разных i), 
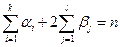. Из теоремы о разложении рациональных дробей на простейшие и интегрирования простейших рациональных дробей следует, что
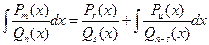, где (4)
, 
,
, 
.
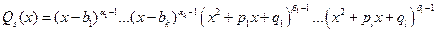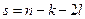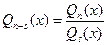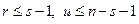Дробь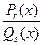 
называется рациональной частью интеграла 
.
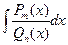М.В.Остроградский предложил следующий способ вычисления интеграла .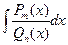
- Находится многочлен
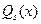(при этом не обязательно раскладывать 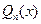на множители): 
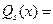НОД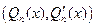 
. - Выписываем
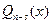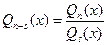: . - Дифференцируем равенство (4), в котором
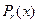и 
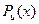записаны с неопределёнными коэффициентами:
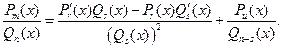
- Умножаем обе части полученного равенства на :
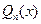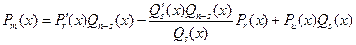, (5)
а так как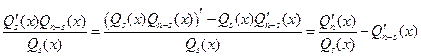 
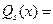, а НОД 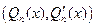, т.е. 
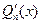делится на 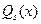, то в правой части равенства (5) стоит полином.
- Приравниваем коэффициенты при одинаковых степенях переменной x в обеих частях равенства (получим систему
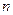уравнений с 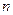неизвестными), откуда и находим коэффициенты 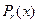и .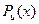
Рассмотрим пример на применение метода Остроградского.
Пример. Найдем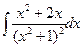 
.
Имеем: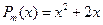 
, 
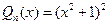
Применяем метод Остроградского:
- ,
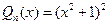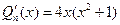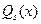, =НОД(, )=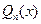 
.
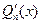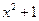Таким образом, = .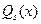
- =
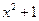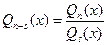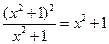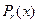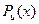. - Запишем равенство (5), где и записаны с неопределёнными коэффициентами:
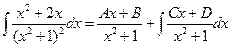(6)
и продифференцируем его:
.
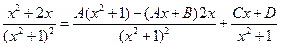- Умножаем на :
,
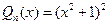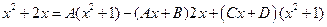откуда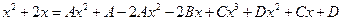 
,
.
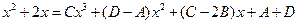- Приравниваем коэффициенты при одинаковых степенях переменной x в обеих частях равенства и находим коэффициенты 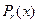и :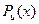
при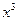 
: 
,
|
|
|
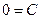при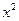 
: 
,
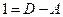при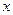 
: 
,
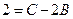при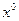 
(свободные коэф-ты): 
.
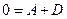Таким образом, получили 4 уравнения с 4 неизвестными:
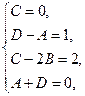
решая которую, находим: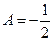 
, 
, 
, 
.
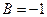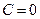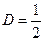Таким образом, подставляя полученные коэффициенты в (6), находим интеграл
.
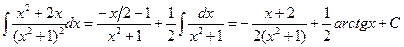Дата добавления: 2015-12-17; просмотров: 27; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!