Интегралы от простейших рациональных дробей вида
(1) вычисляются следующим образом:
a) при 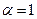
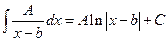 ;
;
b) при 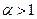
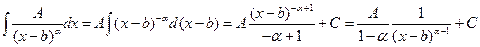 .
.
(2) вычисляются следующим образом:
a) при 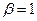
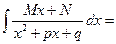
(так как 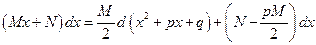 )
)
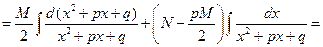
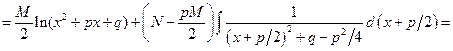
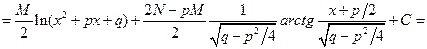
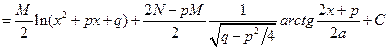 , где
, где 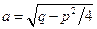 .
.
Заметим, что 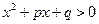 и
и 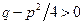 , т.к. трёхчлен
, т.к. трёхчлен 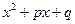 имеет только комплексно сопряжённые корни.
имеет только комплексно сопряжённые корни.
b) при 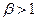
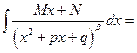
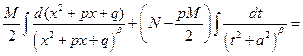
(где 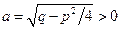 ,
, 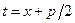 (используем рассуждения из пункта a))
(используем рассуждения из пункта a))
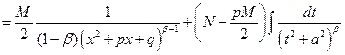 .
.
Вычислим
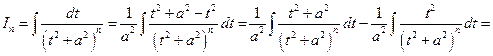
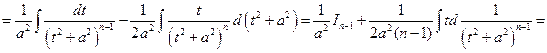
(далее используем формулу интегрирования по частям)
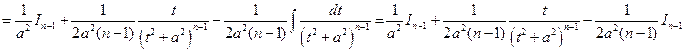 Таким образом, мы получили рекуррентную формулу
Таким образом, мы получили рекуррентную формулу
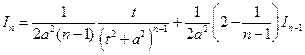 , (3)
, (3)
т.е. формулу, по которой каждый последующий интеграл 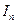 вычисляется через предыдущий
вычисляется через предыдущий 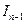 . Поэтому нам достаточно найти
. Поэтому нам достаточно найти 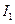 , чтобы мы могли вычислить любой следующий интеграл.
, чтобы мы могли вычислить любой следующий интеграл. 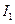 - табличный интеграл:
- табличный интеграл: 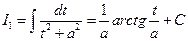 .
.
Возвращаясь к нашему случаю, получаем, что при 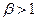
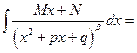
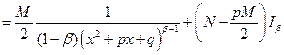 , где
, где 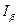 находится по рекуррентной формуле (3) с помощью
находится по рекуррентной формуле (3) с помощью 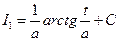 .
.
Используя все вышеприведенные рассуждения, приходим к следующему выводу.
Теорема. Всякая рациональная дробь интегрируется в элементарных функциях.
(Другими словами: интеграл от любой рациональной функции выражается через логарифмическую функцию, арктангенс и рациональную функцию).
Дата добавления: 2015-12-17; просмотров: 12; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
