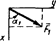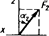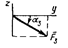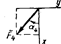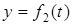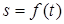Кинематика точки ( краткие сведения из теории)
Таблица С3
| Сила |
|
|
|
| ||||
| Номер условия | F1 = 4 кH | F2 = 6 кH | F3 = 8 кH | F4 = 10 кH | ||||
| Точка прилож. | 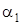 , град. , град.
| Точка прилож. | 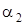 , град. , град.
| Точка прилож. | 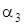 , град. , град.
| Точка прилож. | 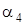 , град. , град.
| |
| 0 | D | 60 | - | - | E | 0 | - | - |
| 1 | H | 90 | D | 30 | - | - | - | - |
| 2 | - | - | E | 60 | - | - | D | 90 |
| 3 | - | - | - | - | E | 30 | H | 0 |
| 4 | E | 0 | - | - | H | 60 | - | - |
| 5 | - | - | D | 60 | H | 0 | - | - |
| 6 | - | - | H | 30 | - | - | D | 90 |
| 7 | E | 30 | H | 90 | - | - | - | - |
| 8 | - | - | - | - | D | 0 | E | 60 |
| 9 | - | - | E | 90 | D | 30 | - | - |
Перед выполнением задания прочтите по учебнику тему: «Произвольная пространственная система сил».
Вопросы, на которые следует обратить внимание и выучить:
1. Момент силы относительно оси, его вычисление. В каких случаях момент силы относительно оси равен нулю? Объясните каждый случай, опираясь на правило вычисления.
2. Какая система сил называется пространственной (произвольной пространственной)?
3. Сформулируйте и запишите уравнения: условия равновесия пространственной системы сил в векторной и алгебраической (координатной) формах.
Пример С3. Вертикальная прямоугольная плита весом Р (рис. C2) закреплена сферическим шарниром в точке А, цилиндрическим (подшипником) в точке В и невесомым стержнем DD', лежащим в плоскости, параллельной плоскости yz. На плиту действуют сила 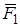 (в плоскости xz), сила
(в плоскости xz), сила 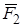 , (параллельная оси у)и пара сил с моментом М (в плоскости плиты).
, (параллельная оси у)и пара сил с моментом М (в плоскости плиты).
|
|
|
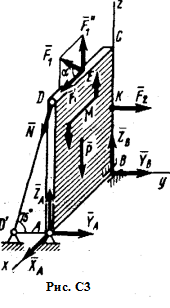
| Дано: Р= 5 кН, М= 3 кН ×м, F1= 6 кН, F2 = 7,5 кН, а = 30°, AВ = 1 м, ВС= 2 м, СЕ = 0,5 АВ, ВК = 0,5 ВС. Определить : реакции опор А, В и стержня DD'. |
Решение. Рассмотрим равновесие плиты. На нее действуют:
а) активные силы 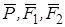 и пара сил, момент которой М;
и пара сил, момент которой М;
б) реакции связей: реакцию сферического шарнира A разложим на три составляющие 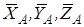 , цилиндрического шарнира (подшипника) B – на две составляющие
, цилиндрического шарнира (подшипника) B – на две составляющие 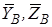 (в плоскости, перпендикулярной оси подшипника), реакцию
(в плоскости, перпендикулярной оси подшипника), реакцию 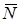
 стержня направим вдоль стержня, предполагая, что он растянут.
стержня направим вдоль стержня, предполагая, что он растянут.
Силы, приложенные к плите, образуют пространственную систему сил. Составляем уравнения ее равновесия:


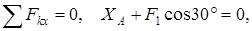 (1)
(1)
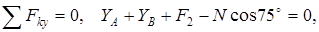 (2)
(2)
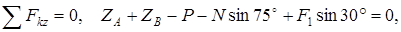 (3)
(3)
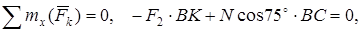 (4)
(4)
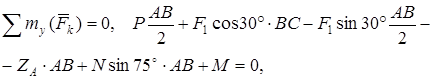 (5)
(5)
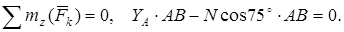 (6)
(6)
Для определения момента силы 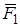 относительно оси y раскладываем
относительно оси y раскладываем 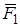 на составляющие
на составляющие 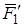 и
и 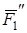 , параллельные осям х и z (
, параллельные осям х и z ( 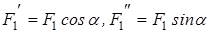 ), и применяем теорему Вариньона (относительно оси). Аналогично можно поступить при определении моментов реакции
), и применяем теорему Вариньона (относительно оси). Аналогично можно поступить при определении моментов реакции 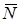 .
.
Подставив в уравнения (1)-(6) числовые значения заданных величин и решив эти уравнения, найдем величины реакций связей.
|
|
|
В своей задаче систему уравнений (1)-(6) следует решить полностью и с пояснениями. Сделайте проверку, например, составив уравнение моментов относительно оси x1, проведенной параллельно оси x.
Ответ: ХА = -5,2 кН, YA = 3,8 кН, ZA = 28,4 кН, YB = -7,5 кН, ZB = -12,4 кН, N = 14,5 кН, Знаки указывают, что силы 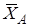 ,
, 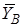 и
и 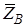 направлены противоположно показанным на рис. C2.
направлены противоположно показанным на рис. C2.
Вопросы для самоконтроля по статике
1. Предмет статики. Основные понятия статики (абсолютно твердое тело, сила, эквивалентные и уравновешенные системы сил, равнодействующая, внешние и внутренние силы). Аксиомы статики. Теорема об уравновешивании двух сходящихся сил третьей силой.
2. Несвободное твердое тело. Связи и реакции связей, виды связей.
3. Проекция силы на ось и на плоскость.
4. Система сходящихся сил. Геометрический и аналитический (координатный) способы нахождения равнодействующей. Условия равновесия системы сходящихся сил в векторной, графической и аналитической формах.
5. Алгебраический момент силы относительно точки. Момент силы относительно центра как вектор.
6. Момент силы относительно оси; случаи равенства нулю этого момента.
|
|
|
7. Пара сил. Алгебраический момент пары сил. Момент пары сил как вектор.
8. Условие эквивалентности пар сил (без доказательства). Свойства пары сил.
9. Теорема о параллельном переносе силы.
10. Приведение произвольной системы сил к данному центру. Главный вектор и главный момент системы сил и их нахождение.
11. Частные случаи приведения системы сил к центру (равнодействующая, пара сил, динамический винт) (без доказательства).
12. Теорема Вариньона о моменте равнодействующей силы относительно центра и оси (без доказательства).
13. Условия равновесия произвольной пространственной системы сил в векторной и аналитической (координатной) формах.
14. Частные случаи уравнений равновесия (плоская система сил, система параллельных сил на плоскости и в пространстве).
КИНЕМАТИКА
В кинематике рассматривается движение точек, тел и механических систем без учета действующих сил (геометрия движения).
В отличие от статики, темы задач разные; поэтому краткие сведения из теории помещены в каждой задаче.
Задача К1
(тема : “Кинематика точки ”)
Под номером К1 помещены две задачи К1а и К1б.
Задача К1а . Точка В движется в плоскости ху (рис. К1.0-К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х= f1 (t), у = f2 (t), где х и у выражены в сантиметрах, t – в секундах (координатный способ задания движения точки). Зависимость х=f1 (t) указана непосредственно на рисунках, а зависимость у = f2 (t) дана в табл. К1.
|
|
|
Найти уравнение траектории точки, а для момента времени t1 = 1с определить координаты, скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Выполнить чертеж, на котором построить траекторию точки, отметить положение точки при t1 = 1с и в этом положении построить все найденные векторы.
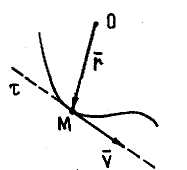
Задача К1б . Точка движется по дуге окружности радиуса 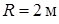 по закону
по закону 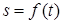 , заданному в таблице К1 (s – в метрах, t – в секундах), где
, заданному в таблице К1 (s – в метрах, t – в секундах), где 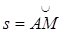 – расстояние точки от некоторого начала A, измеренное вдоль дуги окружности (естественный способ задания движения точки). Определить скорость, нормальное, касательное и полное ускорение точки в момент времени
– расстояние точки от некоторого начала A, измеренное вдоль дуги окружности (естественный способ задания движения точки). Определить скорость, нормальное, касательное и полное ускорение точки в момент времени 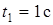 . Изобразить на рисунке векторы
. Изобразить на рисунке векторы 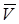 ,
, 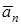 ,
, 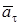 ,
, 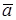 , считая, что точка в этот момент находится в положении M, а положительное направление отсчета s – от A к M. Установить характер движения точки по траектории при
, считая, что точка в этот момент находится в положении M, а положительное направление отсчета s – от A к M. Установить характер движения точки по траектории при 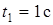 (ускоренное или замедленное).
(ускоренное или замедленное).
Таблица К1
| Номер условия |
|
| ||
| Рис. 0-2 | Рис. 3-6 | Рис. 7-9 | ||
| 0 | 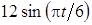
| 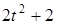
| 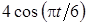
| 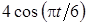
|
| 1 | 
| 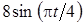
| 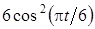
| 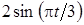
|
| 2 | 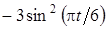
| 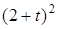
| 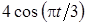
| 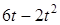
|
| 3 | 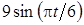
| 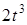
| 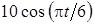
| 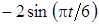
|
| 4 | 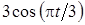
| 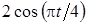
| 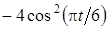
| 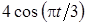
|
| 5 | 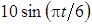
| 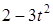
| 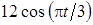
| 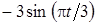
|
| 6 | 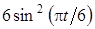
| 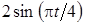
| 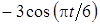
| 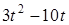
|
| 7 | 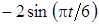
| 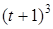
| 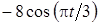
| 
|
| 8 | 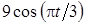
| 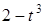
| 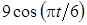
| 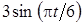
|
| 9 | 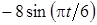
| 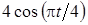
| 
| 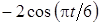
|
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.
В данной задаче все искомые величины нужно определить только для момента времени t1 = 1 с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы: cos 2a= 1 – 2sin2a = 2 cos2a- 1; sin 2a = 2sin a×cos a.
В задаче К1а чертеж следует выполнить на клетчатой или миллиметровой бумаге, указав масштабы длины, скорости и ускорения.
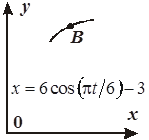 Рис . К1 .0
Рис . К1 .0
| 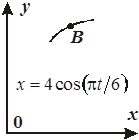 Рис . К1 .1
Рис . К1 .1
| 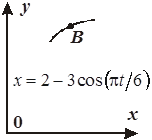 Рис . К 1.2
Рис . К 1.2
|
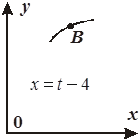 Рис . К 1.3
Рис . К 1.3
| 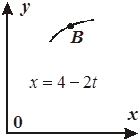 Рис . К1 .4
Рис . К1 .4
| 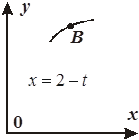 Рис . К1 .5
Рис . К1 .5
|
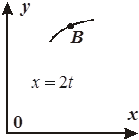 Рис . К 1.6
Рис . К 1.6
| 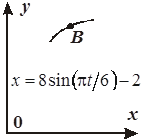 Рис . К1 .7
Рис . К1 .7
| 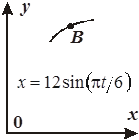 Рис . К 1.8
Рис . К 1.8
|
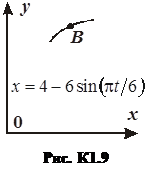
Перед выполнением задания прочтите по учебнику тему: «Кинематика точки».
Вопросы, на которые следует обратить внимание и выучить:
1. Что означает задать движение точки?
2. Три основных способа задания движения точки (векторный, координатный, естественный).
3. Объясните, как в каждом из способов задать движение точки (уравнения движения);
4. Как определяются траектория точки, ее скорость 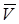 и ускорение
и ускорение 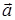 (величина и направление) в каждом способе?
(величина и направление) в каждом способе?
5. Поясните, как строятся естественные оси (в какой точке находится начало координат, каково направление каждой оси);
6. Каков физический смысл векторов 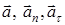 ;
;
7. Поясните, как определить характер движения точки по траектории (ускоренное или замедленное).
Кинематика точки ( краткие сведения из теории)
Задать движение точки - это значит указать способ, позволяющий определить положение точки в любой момент времени относительно выбранной системы отсчета.
Три основных способа задания движения точки: векторный, координатный, естественный.
| Способ задания движения точки. | Задание движения. Уравнения движения точки. | Определение траектории точки. | Определение скорости точки ( 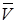 ). ).
| Определение ускорения точки ( 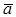 ). ).
|
| Векторный способ |
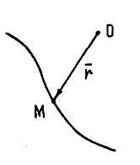
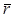 - радиус-вектор, проведенный из не- подвижного центра O в точку M, которая движется. - радиус-вектор, проведенный из не- подвижного центра O в точку M, которая движется.
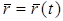 - уравнение
движения точки в
векторной форме. - уравнение
движения точки в
векторной форме.
| Траектория точки -
геометрическое место концов
радиуса-вектора 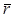 , следящего за движе-нием точки (линия, которую движу-щаяся точка описы-вает в простран-стве). , следящего за движе-нием точки (линия, которую движу-щаяся точка описы-вает в простран-стве).
| 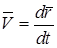 ; направлен вектор ; направлен вектор 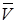 по касатель- ной к траектории в данной точке в сто- рону движения точки. по касатель- ной к траектории в данной точке в сто- рону движения точки.
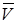 характеризует
быстроту изменения характеризует
быстроту изменения
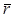 по величине и
направлению. по величине и
направлению.
| 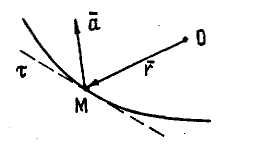 Вектор
Вектор 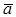 характеризует быстроту изменения характеризует быстроту изменения 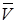 по величине и направ-лению. по величине и направ-лению.
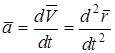 ;
Вектор ;
Вектор 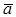 направлен в сторону вогнутости траектории, расположен в соприкасающейся плоскости. Если точка при движении остается в плоскости, то вектор направлен в сторону вогнутости траектории, расположен в соприкасающейся плоскости. Если точка при движении остается в плоскости, то вектор 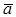 лежит в этой плоскости. лежит в этой плоскости.
|
| Координат- ный способ |
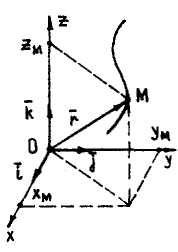
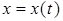 уравнения уравнения
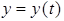 движения движения
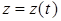 точки M
в координат-
ной форме. точки M
в координат-
ной форме.
| Траектория точки - это линия, которую описывает точка при движении. Уравнение линии получим, исключив параметр t из урав-нений движения; или строим линию по точкам, подстав-ляя значения t в уравнения движе-ния. |
Уравнения движения позволяют определить проекции 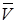 на оси,
затем величину и на-правление. на оси,
затем величину и на-правление.
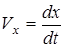 ; ; 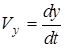 ; ;
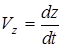 ; модуль: ; модуль:
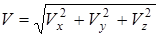 ; ;
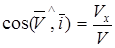 ; ;
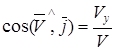
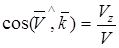
|
Проекции 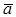 на координатные оси: на координатные оси:
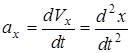 ; ; 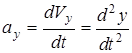 ; ;
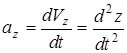 ; модуль: ; модуль:
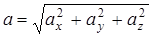 ; ;
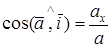 ; ; 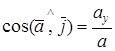 ; ;
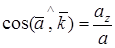 . .
|
 Естествен-
ный способ Естествен-
ный способ
|
Траектория известна заранее и считается криволинейной
осью s. На траекто-рии указано начало отсчета коорди-
наты s (ноль 0), на-
правление отсчета s (+, -);
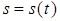 - уравнение (закон) движения точки по траектории. - уравнение (закон) движения точки по траектории.
| Траектория известна. |
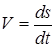 ; если ; если 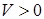 , то точка движется в сторону положитель-ных значений s ; если , то точка движется в сторону положитель-ных значений s ; если
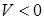 , - точка движет-ся в сторону отрица-тельных значений s; вектор , - точка движет-ся в сторону отрица-тельных значений s; вектор 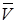 направлен по касательной к траектории в данной точке. направлен по касательной к траектории в данной точке.
| Естественные оси: начало осей в том месте, где находится движу-щаяся точка М. Ось 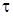 направлена по касательной к траектории. Ось n - главная нормаль - направлена по касательной к траектории. Ось n - главная нормаль - 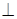 к оси к оси 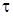 , расположена в соприкасающейся плоскости; направлена в сторону вогнутости траектории. Ось b - би-
нормаль - , расположена в соприкасающейся плоскости; направлена в сторону вогнутости траектории. Ось b - би-
нормаль - 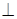 к плоскости к плоскости 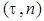 . .
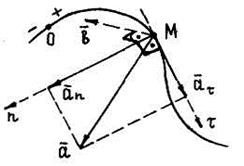 Проекции
Проекции 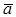 на естественные оси: на естественные оси:
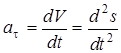 ; ; 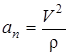 ; ; 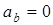 ; при ; при 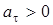 вектор вектор 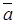 направлен в сторону положительных значений s; направлен в сторону положительных значений s;
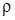 - радиус кривизны траектории в точке М. Если знаки - радиус кривизны траектории в точке М. Если знаки 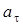 и V совпадают, то движение точки ускоренное, в противном случае - замедленное. и V совпадают, то движение точки ускоренное, в противном случае - замедленное. 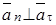 ; ; 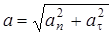 . .
|
Пример К1 a . Уравнения движения точки в плоскости заданы координатным способом и имеют вид:
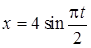 , (1)
, (1)
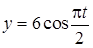 , (2)
, (2)
где время t задано в секундах, координаты x, y – в метрах.
Найти: уравнение траектории точки; положение точки на траектории при 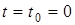 (начальное положение) и при
(начальное положение) и при 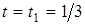 c; скорость
c; скорость 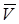 точки; ускорение
точки; ускорение 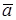 точки; касательное
точки; касательное 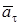 , нормальное
, нормальное 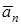 ускорения точки и радиус кривизны траектории
ускорения точки и радиус кривизны траектории 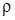 при
при 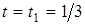 c. В каждом пункте выполнить соответствующие построения на рисунке.
c. В каждом пункте выполнить соответствующие построения на рисунке.
Решение. 1. Найдем уравнение траектории, исключив из (1) и (2) параметр t – время. Способ исключения t зависит от вида функций в правых частях (1), (2). В данном случае найдем из (1), (2) соответственно
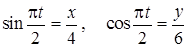 .
.
Возводя полученные соотношения в квадрат, после этого складывая их и учитывая, что 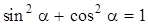 , найдем:
, найдем:
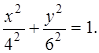
Из этого уравнения следует, что траекторией точки является эллипс, полуоси которого равны 4 м и 6 м, а центр имеет координаты (0, 0).
Выберем масштаб координат и выполним рисунок. Следует заметить, что приведенный рисунок (Рис. К1а) имеет вид, соответствующий уже окончанию решения; свой рисунок рекомендуется делать по мере продвижения решения. Это позволяет контролировать получаемые результаты и делает их более наглядными.
2. Находим положение точки при 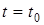 , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):
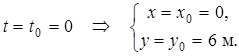
3. Находим положение точки при 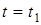 , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):
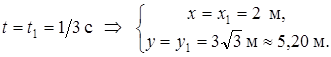
Указываем на рисунке точки 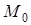 и
и 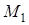 , учитывая масштаб координат.
, учитывая масштаб координат.
4. Найдем скорость точки. Из теории следует, что при координатном способе задания движения определяются сначала проекции скорости на оси координат. Используя (1) и (2) – уравнения движения точки – находим
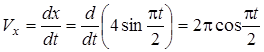 , (3)
, (3)
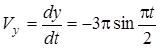 . (4)
. (4)
Модуль скорости 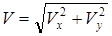 . Подставляя сюда (3), (4), получим
. Подставляя сюда (3), (4), получим
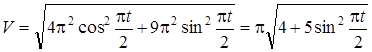 . (5)
. (5)
При 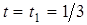 с :
с : 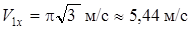 ,
, 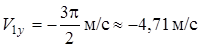 ,
,
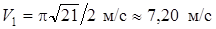 . (6)
. (6)
Выберем масштаб для скоростей (рис. К1а), проведем в точке M1 линии параллельные осям x и y, и на этих линиях в масштабе скоростей отложим отрезки: 5,44 по оси x и - 4,71 по оси y, что соответствует величинам и знакам найденных проекций вектора скорости. На этих составляющих строим параллелограмм (прямоугольник), диагональ которого по величине и направлению соответствует вектору 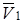 . Проверьте следующее: длина построенного вектора должна получиться равной найденному значению
. Проверьте следующее: длина построенного вектора должна получиться равной найденному значению 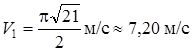 (с учетом масштаба скоростей). Вектор
(с учетом масштаба скоростей). Вектор 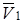 направлен по касательной к траектории в точке
направлен по касательной к траектории в точке 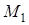 и показывает направление движения точки по траектории.
и показывает направление движения точки по траектории.
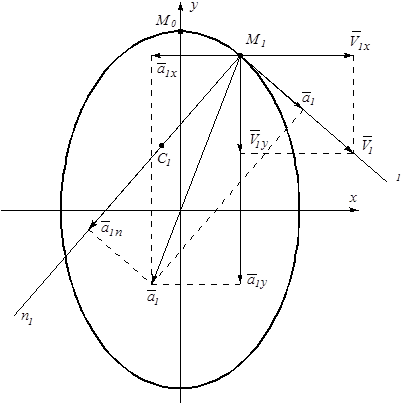 Масштаб длины: _____ =1м, скорости ___ =1м/с, ускорения: __ =1м/с2
Рис . К 1а. Масштаб длины: _____ =1м, скорости ___ =1м/с, ускорения: __ =1м/с2
Рис . К 1а.
| В точке 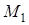 именно сейчас построим естественные оси: касательную именно сейчас построим естественные оси: касательную 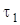 и главную нормаль и главную нормаль 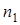 (эти оси потребуются позже). Каса-тельную (эти оси потребуются позже). Каса-тельную 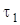 проводим вдоль проводим вдоль 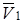 ; главную нормаль ; главную нормаль 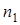 проводим перпендикулярно проводим перпендикулярно 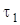 в плоскости рисунка и направляем к центру кривизны траектории в точке в плоскости рисунка и направляем к центру кривизны траектории в точке 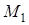 (в сторону вогнутости траектории). (в сторону вогнутости траектории).
|
5. Находим ускорение точки, используя (3), (4):
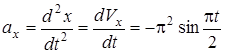 , (7)
, (7)
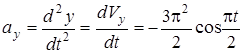 . (8)
. (8)
Модуль ускорения 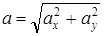 . Из (7), (8) получим
. Из (7), (8) получим
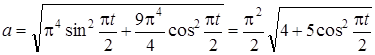 . (9)
. (9)
Подставляя в (7) - (9) 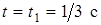 , найдем
, найдем
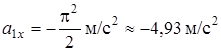 ,
, 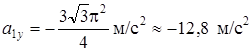 ,
,
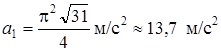 . (10)
. (10)
В точке 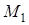 строим в масштабе проекции ускорений
строим в масштабе проекции ускорений 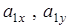 , учитывая их величины и знаки, а затем строим вектор ускорения
, учитывая их величины и знаки, а затем строим вектор ускорения 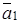 . Построив
. Построив 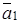 , следует проверить, получилось ли на рисунке
, следует проверить, получилось ли на рисунке 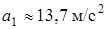 (c учетом масштаба ускорений), и направлен ли вектор
(c учетом масштаба ускорений), и направлен ли вектор 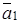 в сторону вогнутости траектории (вектор
в сторону вогнутости траектории (вектор 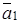 проходит через центр эллипса, но это есть особенность данной задачи, связанная с конкретным видом функций (1) и (2)).
проходит через центр эллипса, но это есть особенность данной задачи, связанная с конкретным видом функций (1) и (2)).
6. Находим касательное ускорение 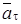 , характеризующее изменение модуля
, характеризующее изменение модуля 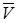 .
.
Учитывая (5), получим 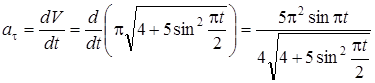 .
.
При 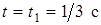
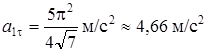 . (11)
. (11)
Касательное ускорение можно также найти, дифференцируя по времени равенство 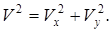 Получим
Получим
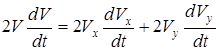 , откуда следует
, откуда следует
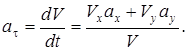
Нормальную составляющую 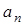 ускорения, характеризующую изменение направления
ускорения, характеризующую изменение направления 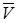 , можно найти по формуле
, можно найти по формуле
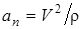 , (12)
, (12)
если 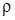 - радиус кривизны траектории заранее известен, или (учитывая, что,
- радиус кривизны траектории заранее известен, или (учитывая, что, 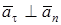 и, следовательно,
и, следовательно, 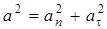 ) по формуле
) по формуле
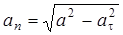 . (13)
. (13)
Так как в данной задаче радиус 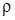 заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
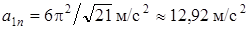 . (14)
. (14)
Вернемся к рис. К1а. Ранее на этом рисунке вектор 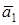 был построен по составляющим
был построен по составляющим 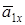 ,
, 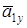 . С другой стороны, этот вектор можно разложить на составляющие по естественным осям
. С другой стороны, этот вектор можно разложить на составляющие по естественным осям 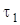 и
и 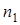 (пользуясь правилом параллелограмма). Выполним это разложение и построим на рисунке векторы
(пользуясь правилом параллелограмма). Выполним это разложение и построим на рисунке векторы 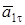 и
и 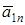 . Далее следует провести проверку: с учетом масштаба ускорений определить по рисунку величины
. Далее следует провести проверку: с учетом масштаба ускорений определить по рисунку величины 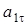 ,
, 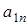 и убедиться, что они совпадают с (11), (14).
и убедиться, что они совпадают с (11), (14).
Заметим, что движение точки ускоренное, т.к. направления векторов 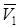 и
и 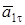 совпадают (рис. К1а).
совпадают (рис. К1а).
Найдем радиус кривизны 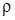 , используя (12), откуда следует, что
, используя (12), откуда следует, что 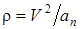 . Подставляя в последнее соотношение
. Подставляя в последнее соотношение 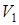 и
и 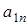 из (6) и (14), получим радиус кривизны траектории в точке
из (6) и (14), получим радиус кривизны траектории в точке 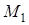 :
: 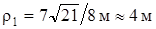 . Отложим на рисунке от точки
. Отложим на рисунке от точки 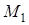 по оси
по оси 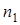 отрезок
отрезок 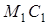 длины
длины  (в масштабе длин); полученная точка
(в масштабе длин); полученная точка 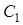 есть центр кривизны траектории в точке
есть центр кривизны траектории в точке 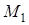 .
.
Объединяя полученные результаты, запишем
Ответ :
1. траектория точки - эллипс, имеющий уравнение 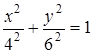 ;
;
2. 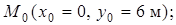
3. 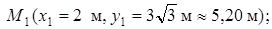
4. 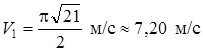 ;
;
5. 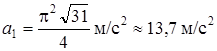 ;
;
6. 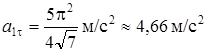 ;
; 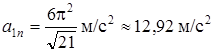 ;
;
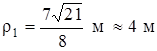 .
.
Обсудим некоторые особенности и частные случаи, которые могут встретиться в задачах.
Если траектория точки – прямая линия, то 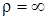 и, следовательно,
и, следовательно, 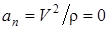 . Найденное по величине и направлению ускорение
. Найденное по величине и направлению ускорение 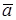 равно ускорению
равно ускорению 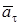 .
.
Если траектория точки – окружность, то 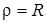 , где R – радиус окружности (определяется из уравнения траектории). Если скорость V точки найдена, то
, где R – радиус окружности (определяется из уравнения траектории). Если скорость V точки найдена, то 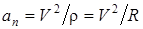 . Вектор
. Вектор 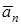 направлен к центру окружности. Касательное ускорение
направлен к центру окружности. Касательное ускорение 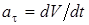 , полное ускорение
, полное ускорение 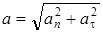 .
.
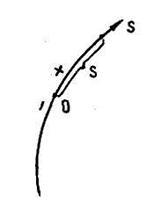
Пример К1б. Точка движется по дуге окружности радиуса 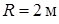 по закону
по закону 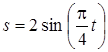 (s – в метрах, t – в секундах), где
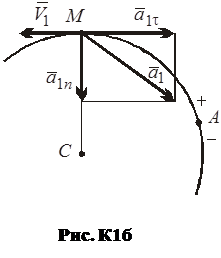
(s – в метрах, t – в секундах), где 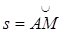 (рис. К1б).
(рис. К1б).
Определить : скорость и ускорение точки в момент времени 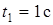 ; характер движения точки по траектории (ускоренное или замедленное).
; характер движения точки по траектории (ускоренное или замедленное).
 Решение. Определяем скорость точки:
Решение. Определяем скорость точки:
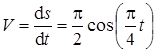 .
.
При 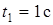 получим
получим 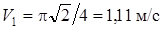 .
.
Ускорение находим по его касательной и нормальной составляющим:
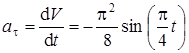 ,
,
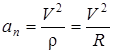 .
.
При 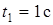 получим, учитывая, что
получим, учитывая, что 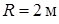 ,
,
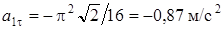 ,
, 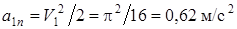 .
.
Тогда ускорение точки при 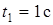 будет
будет
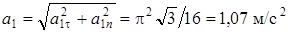 .
.
Изобразим на рис. К1б векторы 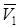 ,
, 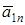 ,
, 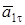 ,
, 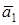 , считая положительным направление от A к M. Так как
, считая положительным направление от A к M. Так как 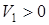 ,
, 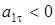 , то движение точки замедленное.
, то движение точки замедленное.
Ответ: 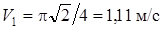 ;
; 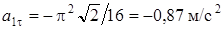 ;
;
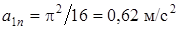 ; движение точки замедленное.
; движение точки замедленное.
Примечание : одна из частей задачи К3 (см. ниже) аналогична задаче К1б.
Задача К2
Дата добавления: 2022-12-03; просмотров: 111; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!