Задание 1. Используя схему Горнера, многочлен f( x) разделите на x- c. Выпишите частное, остаток. Выясните, является ли число c корнем многочлена f( x).
Вариант 2.
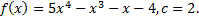
Решение.
Вычисления по схеме Горнера имеют вид
| 5 | -1 | 0 | -1 | -4 | |
| 2 | 5 | 9 = 2 * 5 - 1 | 18 = 2 * 9 + 0 | 35 = 2 * 18 - 1 | 66 = 2 * 35 - 4 |
Следовательно,
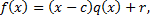
где
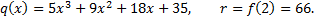
Значит, число 2 не является корнем многочлена f(x).
Задание 2. Найдите линейное представление наибольшего общего делителя (НОД) многочленов f( x) и g( x).
Вариант 2.
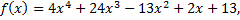
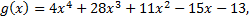
Решение.
Для нахождения НОД многочленов воспользуемся алгоритмом Евклида.
Шаг 1. Разделим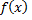 
на 
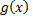с остатком:
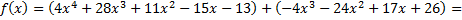
остаток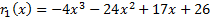 
.
Шаг 2. Разделим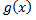 
на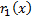 
с остатком:
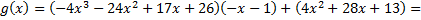
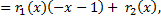
остаток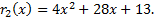 
Шаг 3. Разделим 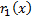на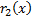 
с остатком:
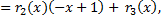
остаток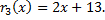 
Шаг 4. Разделим 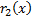на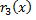 
с остатком:
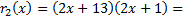
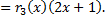
На этом шаге остаток равняется нулю. Это означает, что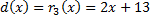 
является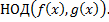 
Найдем его линейное представление.
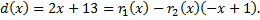
Заменим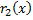 
его выражением через 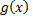и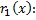 
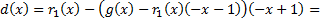
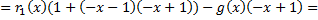
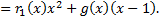
Заменим 
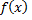его выражением через и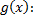 
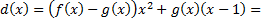
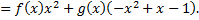
Отсюда следует, что искомые многочлены, входящие в линейное представление НОД
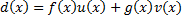
имеют вид:
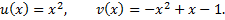
Сделаем проверку:
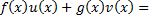
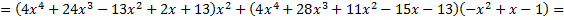
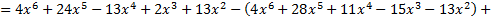
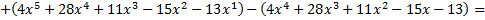
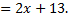
Ответ: 
Задание 3. Пользуясь алгоритмом Евклида, освободитесь от иррациональности в знаменателе данной дроби.
Вариант 2.
Решение.
Знаменатель данной дроби имеет вид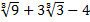 
, то есть содержит иррациональное число 
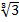. Нам нужно дробь привести к виду, чтобы в знаменателе не было иррационального числа. Для этого необходимо подобрать такой сомножитель, после умножения на который в знаменателе получится рациональное число. С этой целью введем многочлены 
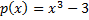(корнем которого является число 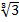) и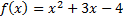 
(значение которого при 
стоит в знаменателе данной дроби).
|
|
|
Многочлен 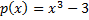неприводим над полем Q, поскольку он третьей степени и не имеет рациональных корней. Действительно, рациональными корнями этого многочлена могут быть лишь числа 
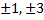, а подстановкой легко убедиться, что ни одно из них не является корнем.
Поскольку многочлен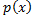 
неприводим, а степень многочлена 
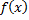равна 2 и меньше степени 
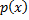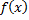, то и 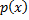- взаимно-простые многочлены.
Найдем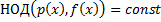 
по алгоритму Евклида.
Шаг 1. Разделим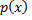 
на 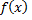с остатком:
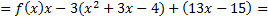
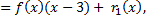
остаток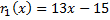 
.
Шаг 1. Разделим 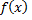на 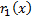с остатком:
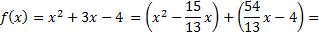
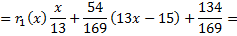
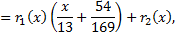
остаток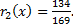 
Отсюда следует, что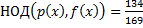 
. Найдем его линейное представление.
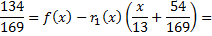
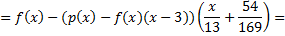
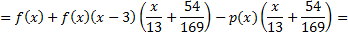
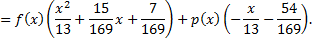
Так как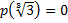 
, то отсюда следует, что
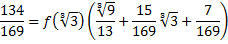
или
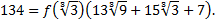
Таким образом, мы нашли сомножитель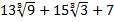 
, после умножения на который в знаменателе данной дроби получится число 134.
Получаем, что данная дробь равна:
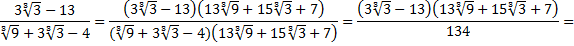
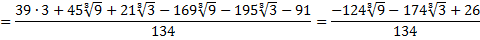
В знаменателе полученного числа нет иррациональности. Проверим полученный результат. Для этого найдем произведение:
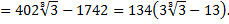
Это значит, что
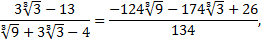
то есть все вычисления верны.
Ответ: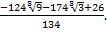 
Задание 4. Найдите разложения многочленов f( x), g( x) на неприводимые множители над полями Q, R, C.
Вариант 2.
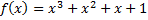
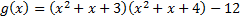
Решение.
Разложим многочлен 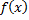на неприводимые множители над полем С:
|
|
|
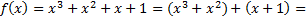
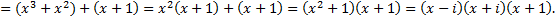
Над полем R многочлен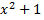 
является неприводимым, поскольку не имеет действительных корней, поэтому разложение 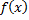на неприводимые множители над полем R имеет вид:
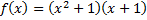
Это же разложение является разложением 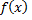на неприводимые множители и над полем Q, так как коэффициенты входящих в него множителей рациональные.
Ответ:
· над полем Q: ;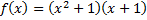
· над полем R: ;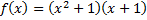
· над полем C: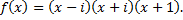 
Теперь рассмотрим многочлен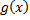 
. Обозначим 
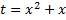, тогда:
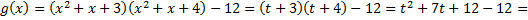
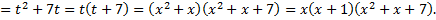
Преобразуем квадратный трехчлен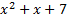 
путем выделения полного квадрата:
Он не имеет действительных корней, и, таким образом, над полями Q и R неприводим, а разложение многочлена 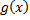на неприводимые множители над этими полями имеет, следовательно, вид:
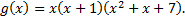
Над полем С имеем:
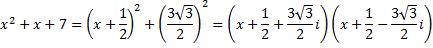
Поэтому разложение многочлена 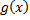на неприводимые множители над полем С:
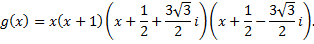
Ответ:
· над полем Q: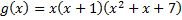 
;
· над полем R: ;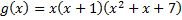
· над полем C: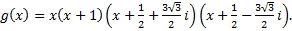 
Задание 5. Решите уравнение f(x)=0 методом Кардано и разложите f( x) на неприводимые множители над полями R и С.
Вариант 2.
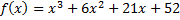
Решение.
Сделаем замену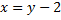 
и получим:
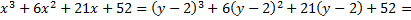
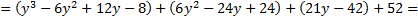
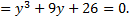
Неизвестное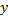 
ищем в виде 
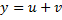, и тогда наше уравнение запишется следующим образом:
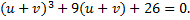
Раскрыв скобки и перегруппировав члены, получим
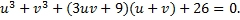
Предположим, что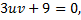 
т.е.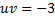 
(так что 
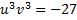). Тогда 
.
|
|
|
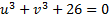Таким образом, имеем
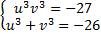
Мы видим, что числа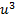 
и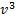 
являются корнями квадратного уравнения 
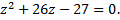Решая это уравнение, находим его корни: 
Тогда:
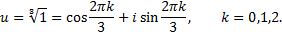
Значит,
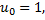
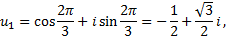
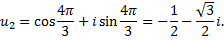
Тогда,
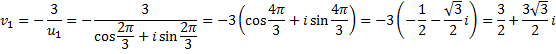
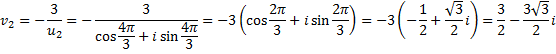
Теперь, складывая каждое значение 
с соответствующим значением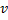 
, получим три корня неполного кубического уравнения:
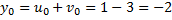
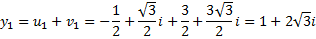
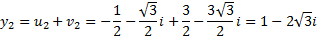
Но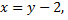 
поэтому корнями исходного уравнения будут
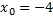
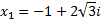
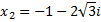
Таким образом, разложение над полем С имеет вид
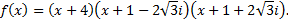
Чтобы найти разложение над полем R, разделим многочлен 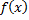на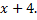 
Тогда разложение над полем R будет иметь вид
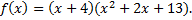
Задание 6. Решите уравнение f(x)=0 методом Феррари и разложите f( x) на неприводимые множители над полями R и С.
Вариант 2.
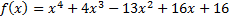
Решение.
Переносим в правую часть уравнения с противоположными знаками все члены, степени которых не выше двух:
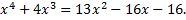
Если к обеим частям последнего уравнения прибавить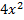 
, то в левой части получится полный квадрат:
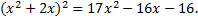
Пока в правой части уравнения нет полного квадрата. Чтобы получить равенство с полными квадратами в обеих частях, введем параметр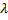 
и составим следующий многочлен:
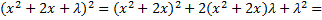
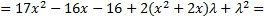
Таким образом, мы нашли равенство
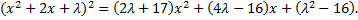
Возьмем параметр 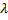таким, чтобы и правая часть была полным квадратом. Для этого надо требовать, чтобы дискриминант квадратного трехчлена в правой части равнялся нулю. Имеем
|
|
|
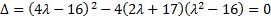
Легко видно, что одним из решений данного уравнения является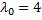 
. Подставляя данное значение, получим:
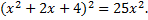
Это уравнения распадается на два квадратных уравнения:
Решая эти уравнения, получаем все четыре корня данного уравнения четвертой степени:
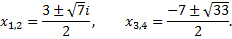
Таким образом, разложение 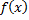над полем С имеет вид:
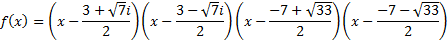
А над полем R:
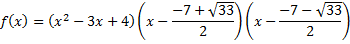
Дата добавления: 2022-11-11; просмотров: 71; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!