Задание 4, б) Найдите корни уравнения в поле комплексных чисел и изобразите их геометрически.
Задание 1. Решите данные уравнения.
Вариант 2.
а)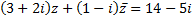 
б) 
Решение.
а) Неизвестное комплексное число z будем искать в алгебраической форме 
. Тогда 
, где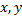 
– соответственно действительная и мнимая части комплексного числа 
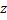, пока неизвестные действительные числа. Подставляя в данное уравнение выражения для 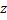и 
, получим:
Выполним указанные действия в левой части уравнения и запишем в алгебраической форме:
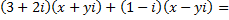
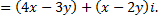
Тогда заданное уравнение примет вид:
Приравнивая соответственно действительные и мнимые части в последнем равенстве, получим систему уравнений:
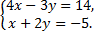
Найдем решение системы по правилу Крамера:
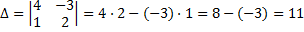
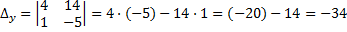
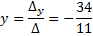
Таким образом, единственным решением данного уравнения будет комплексное число
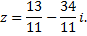
Ответ: 
Проверка:
.
б) По формуле 
нахождения корней квадратного уравнения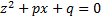 
, находим: 
, где
Теперь нужно вычислить 
, то есть алгебраическую форму записи этого комплексного числа. Пусть 
, здесь 
. Тогда, 
, то есть 
. Приравнивая соответственно действительные и мнимые части, получим систему уравнений относительно неизвестных x и y:
Кроме того,
По известным сумме и разности чисел 
и 
находим: 
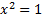и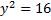 
, то есть 
и
, откуда, учитывая, что 
, находим решения:
Подставляя полученные значения x и y в выражения 
и 
, найдем решения данного уравнения:
Ответ: 
Проверка:
Задание 2. Изобразите на комплексной плоскости множество всех точек,
удовлетворяющих заданным условиям.
|
|
|
Вариант 2.
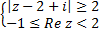
Решение.
Рассмотрим вначале первое условие. Комплексное число z в алгебраической форме имеет вид 
Тогда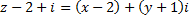 
. Откуда, по определению модуля комплексного числа, получим 
или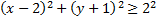 
. Множество точек 
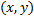, удовлетворяющих этому неравенству, есть множество точек, расположенных вне круга радиуса 2 с центром в точке (2, -1) или на соответствующей граничной окружности.
Второму условию удовлетворяют все комплексные числа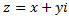 
, для которых 
. Эти неравенства задают полосу, лежащую между вертикальными прямым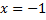и 
и 
. При этом точки прямой 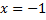входят в множество (неравенство 
нестрогое), а точки прямой 
- не входят в него (неравенство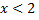 
строгое).
Множеством точек, удовлетворяющих обоим заданным условиям, будет пересечение двух множеств (внешности круга и полосы):
Задание 3. Вычислите значение данного выражения.
Вариант 2.
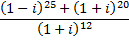
Решение.
Возведение в степень комплексных чисел легче выполнить в тригонометрическом виде. Поэтому, числа данного выражения запишем в тригонометрической форме:
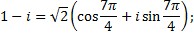
Тогда при помощи формулы возведения в степень комплексного числа (формула Муавра), получим, во-первых:
во-вторых:
и наконец:
|
|
|
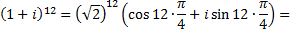
Подставляя полученные выражения в исходное, имеем:
Ответ: 
Задание 4, a) Найдите значение функции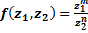 
для заданных значений 
Вариант 2.
Решение.
Сначала запишем числа 
и в тригонометрической форме:
Найдем модуль и аргумент числа 
находим из
системы уравнений:
Отсюда имеем: 
.
Найдем модуль и аргумент числа 
находим из
системы уравнений:
Отсюда имеем: 
.
Теперь по формулам Муавра получим:
и
Используя формулу деления комплексных чисел в тригонометрической форме, имеем:
Ответ: 
Задание 4, б) Найдите корни уравнения в поле комплексных чисел и изобразите их геометрически.
Вариант 2.
Решение.
Для того, чтобы решить данное уравнение, воспользуемся формулой вычисления корня n-ой степени из комплексного числа. Представим число 
в тригонометрической форме:
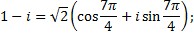
Согласно общей формуле,
где 
Итак, выпишем все корни уравнения:
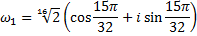
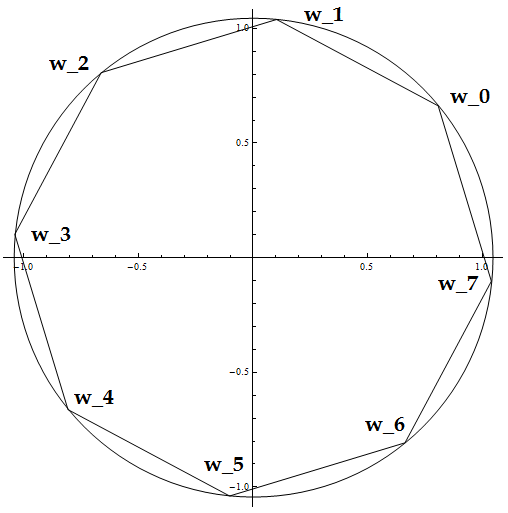
Изобразим полученные корни геометрически. Заметим, что все корни имеют один и тот же модуль, следовательно, все они расположены на окружности радиуса 
, а их аргументы отличаются на один и тот же угол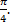 
Поэтому, корни этого уравнения являются вершинами правильного восьмиугольника, вписанного в окружность радиуса 
|
|
|
Дата добавления: 2022-11-11; просмотров: 99; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!