Сечение куба в форме правильного четырёхугольника
-Одним из вариантов построения такого сечения в кубе является квадрат MNKP, стороны которого параллельны рёбрам одной из граней.
Стороны сечения при таком построении будут равны стороне куба.
х = а
- Еще один вариант решения этой задачи – квадрат, построенный под углом.
Как рассчитать сторону такого квадрата? Пусть ребро куба равно а. Из прямоугольного треугольника АВЕ по теореме Пифагора находим сторону искомого сечения:
х =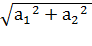 
,
где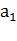 
, 
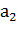- отрезки ребер куба, отсекаемые секущей плоскостью (ЕFG)
Ход построения
Построим сечение куба ABCDA1B1C1D1 плоскостью EFG, где AE=DF.
Шаг 1. Соединим точки E и F, так как они лежат в плоскости грани ADD1A1.
Точка G лежит на прямой BC.
Шаг 2. Прямая EF будет параллельна AD и, следовательно, BC.
Шаг 3. Соединим точки E и B, F и C, так как они лежат в плоскостях ABB1A1 и DCC1D1 соответственно.
Шаг 4. EFGС - искомое сечение куба ABCDA1B1C1D1 плоскостью EFG.
Количество таких сечений неограниченно.
Вывод: существует сечение куба в форме правильного четырехугольника.
Сечение куба в форме правильного пятиугольника
Воспользуемся свойством параллельных плоскостей: если две параллельные плоскости (грани куба) пересечены третьей (сечением), то линии их пересечения параллельны. В правильном пятиугольнике нет пар параллельных сторон. Значит, правильный пятиугольник не может быть сечением куба.
Экспериментальным путем мы это проверили. / Приложение 2. Рис.7/
|
|
|
Построим сечение куба ABCDA1B1C1D1 плоскостью EGH:
Шаг 1. Точки H и G лежат в одной плоскости грани BB1C1С. Соединим эти точки.
Шаг 2. Продолжим прямую HG и ребро BB1. Они пересекутся в точке О, которая будет лежать в плоскостях граней AA1B1B и B1BCC.
Шаг 3. Точки О и Е лежат в одной плоскости грани AA1B1B. Мы можем их соединить.
Прямая ЕО пересечет АВ в точке F. Соединим точки F и G.
Шаг 4. Продолжим прямую FE и ребро А1В1. Они пересекутся в точке О1. Аналогично, GH и B1C1 пересекутся в О2.
Шаг 5. Мы можем соединить точки О1 и О2, так как они лежат в плоскости верхней грани A1B1C1D1.
Получившуюся точка D1 соединяем с точками Е и Н.
Шаг 6. D1HGFE – искомое сечение куба ABCDA1B1C1D1 плоскостью EGH.
Вывод: Сечением куба может быть только неправильный пятиугольник. Количество таких сечений в кубе неограниченно; форма сечения зависит от выбора точек.
Сечение куба в форме правильного шестиугольника
Выполним построение секущей плоскости куба в форме правильного шестиугольника.
Для этого отметим точки - середины рёбер. Найдем сторону такого шестиугольника. Пусть ребро куба а.
Из прямоугольного треугольника АКМ выразим гипотенузу - сторону искомого сечения:
|
|
|
х =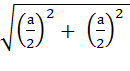 
= 
= 
= 
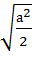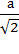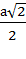
Ход построени:
Построим сечение куба ABCDA1B1C1D1 плоскостью KMN.
Шаг 1. Точки M, N лежат в одной плоскости нижней грани ABCD. Мы можем соединить их.
Точки K и M лежат в одной плоскости передней грани ABA1B1. Мы также можем их соединить.
Шаг 2. Продолжим прямую KM и ребро A1B1. Так как обе прямые лежат в одной передней грани, мы можем соединить их.
Шаг 3. Продолжим прямую NF и B1C1. Они лежат в общей боковой грани и мы можем их соединить.
Шаг 4. Получившиеся точки O1 и O2 лежат в верхней грани, так как ребра A1B1 И B1C1 принадлежат верхней грани. Мы можем соединить данные точки. Данная прямая пересекает ребра A1D1и C1D1 в точках Z и E соответственно.
Шаг 5. Точки K и Z лежат в плоскости боковой грани, точки E и F – в плоскости задней грани. Поэтому мы можем соединить т. K и Z, т. E и F.
Шаг 6. KMNFEZ - искомое сечение куба ABCDA1B1C1D1 плоскостью KMN.
Вывод: существует сечение куба в форме правильного шестиугольника. Количество таких сечений 4.
Экспериментальная часть
Выводы, полученные в ходе математических расчетов и геометрических построений, мы проверили экспериментально. /Приложение2/.
Использование программы GeoGebra позволило наглядно подтвердить верность полученных результатов. /Приложение3/.
|
|
|
Заключение
В ходе практической работы мы пришли к выводу, что наше первоначальное предположение оказалось неверным. В кубе возможно построение сечений только в форме правильных треугольника, четырёхугольника и шестиугольника. Правильный пятиугольник в силу определённых факторов не может быть сечением куба. В ходе экспериментальной проверки эти выводы подтвердились.
Работа над проектом помогла развить пространственное, абстрактное и логическое мышление, пространственное воображение, расширила наши представления о способах построения сечений многогранников. Мы познакомились с возможностями программы GeoGebra, наглядного инструмента в практике геометрических построений. Приобретенные знания и умения позволят усовершенствовать навыки в решении стереометрических задач.
Информационные источники
1. А.А. Прокофьев, А.Г. Корянов. Математика. Многогранники: типы задач и методы их решения – Ростов на Дону, Легион, 2015.
2. Л.С. Атанасян, В.Ф. Бутузов, Геометрия, 10-11: учебник для общеобразовательных учреждений, М.: Просвещение, 2008.
3. Н.М. Резникова, Е.М. Фридман. Математика. ЕГЭ. Профильный уровень. Сечения многогранников: учебное пособие; Ростов на Дону, 2017.
|
|
|
4. Научная библиотека избранных естественно – научных изданий, Геометрические построения на плоскости.
https://scask.ru/k_book_gpl.php?id=2
Дата добавления: 2022-07-16; просмотров: 251; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!