Теоретический обзор актуальных геометрических понятий
Рассмотрим основные геометрические объекты в контексте темы «Сечения многогранников»
· Многогранная поверхность или многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Грани – многоугольники, из которых составлен многогранник. Рёбра – стороны граней, а концы рёбер – вершины многогранника.
· Сечение многогранника – это многоугольник, вершины которого принадлежат рёбрам, а стороны – граням многогранника, при этом две соседние вершины принадлежат одной грани. Сечение многогранника представляет собой множество всех точек пространства, принадлежащих одновременно данным многограннику и секущей плоскости. Так как прямая и плоскость пересекаются в точке, а две плоскости - по прямой, то сечением многогранника плоскостью является плоский многоугольник, вершинами которого служат точки пересечения секущей плоскости с ребрами многогранника, а сторонами - отрезки, по которым секущая плоскость пересекает его грани. Это означает, что для построения искомого сечения данного многогранника плоскостью, достаточно построить точки ее пересечения с ребрами многогранника. Затем последовательно соединить эти точки отрезками.
· Правильный многогранник – выпуклый многогранник, составленный из равных правильных многоугольников; в каждой вершине правильного многогранника сходится одно и то же число рёбер.
|
|
|
· Куб (гексаэдр) – правильный многогранник, составленный из 6 равных квадратов. Все 12 ребер куба равны, двугранные углы прямые. Куб имеет 9 осей симметрии, центр симметрии куба - точка пересечения его диагоналей.
· Сечением правильного многогранника может быть многоугольник, число вершин которого не превышает числа граней многогранника. При этом, число вершин n ≥ 3 (не существует многоугольника, у которого число вершин меньше 2). Следовательно, сечениями куба могут быть n-угольники, где 3≤n ≤ 6 (треугольники, четырехугольники, пятиугольники, шестиугольники). /Приложение1/
Мы предположили, что сечением куба может быть любой правильный n-угольник, где 3≤ n ≤6. Рассмотрим каждый из возможных вариантов и выполним соответствующие построения.
Практическая часть
Сечение куба в форме правильного треугольника
Рассмотрим способы построения сечения куба в форме правильного треугольника.
- Диагональное сечение (линии пересечения секущей плоскости с гранями куба являются диагоналями его трех граней)
Вычислим сторону такого треугольника. Пусть ребро куба равно а. Тогда, по теореме Пифагора в прямоугольном треугольнике AB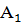 
катеты равны ребру куба а, гипотенуза – стороне сечения. Сторона треугольника (искомое сечение) равна а 
.
|
|
|
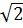х =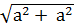 
= 
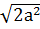= а .
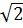- Если секущая плоскость пересекает три ребра куба, выходящие их одной вершины, то в сечении получится треугольник. Он будет правильным, если отсекаемые плоскостью отрезки ребер равны. Количество таких сечений в кубе неограниченно, результат построения зависит от выбора точек на ребре куба.
Ход построения:
- Отметим на 3 ребрах куба, имеющих одну общую вершину, 3 точки, равноудаленные от этой вершины.
- Соединим эти точки отрезками.
Получим сечение куба в форме правильного треугольника. Длину стороны такого треугольника находим по теореме Пифагора:
х =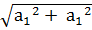 
= 
= 
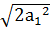, где 
- длина отрезка, отсекаемого секущей плоскостью.
Построим сечение куба ABCDA1B1C1D1 плоскостью NKM.
Шаг 1. Ребра A1B1, B1C1, B1B выходят из одной общей вершины B1. Отметим на этих ребрах точки K, N, M соответственно на равном расстоянии от общей вершины т.В1.
Шаг 2. Точки N и K лежат в плоскости верхней грани A1B1C1D1. Поэтому мы можем их соединить.
Аналогично, соединяем точки K и M, M и N.
MNK - сечение куба ABCDA1B1C1D1 в виде правильного треугольника.
Вывод: существует сечение куба в форме правильного треугольника.
|
|
|
Дата добавления: 2022-07-16; просмотров: 18; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!