Найти вероятность того, что сумма очков, выпавших при бросании двух игральных кубиков, равна 3 или 4.
Решение
Опыт: бросание двух игральных кубиков 
С – сумма выпавших очков равна 3 или 4, С = А + В, где
А - сумма выпавших очков равна 3; А={(1; 2), (2; 1)}
В - сумма выпавших очков равна 4; B={(1;3), (3; 1), (2; 2)}
A, B - несовместные события
По теореме 1: Р(А+В) = Р(А) + Р(В) =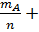 
= 
Ответ: 5/36
Следствия теоремы 1
1. Если события А1, А2, …, Апобразуют полную группу событий, то сумма их вероятностей равна 1:
Р(А1) + Р(А2) +…+Р(Ап) = 1 (3)
2. Сумма вероятностей противоположных событий равна 1:
Р(А) + Р(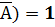 
(4)
Следствие 2 важно в практическом применении, так как часто оказывается легче вычислить Р( 
, чем Р(А). В таких случаях искомую вероятность находят по формуле:
Р(А) = 1 - Р( (5)
Пример 2
Круговая мишень состоит из трех зон. Вероятность попадания в первую зону при одном выстреле равна 0,15, во вторую – 0,23, в третью – 0,17. Найти вероятность промаха при одном выстреле.
Решение
Обозначим события: А – попадание в мишень,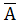 
– промах.
А1 – попадание в первую зону А2 – попадание во вторую зону А3 – попадание в третью зону
|
|
|
А = А1 + А2 + А3
По следствию 2 имеем: Р(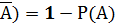 
.
Так как событияА1, А2, А3 – несовместные, по теореме 1 получим:
Р(А) = Р(А1+ А2 + А3) = Р(А1) + Р(А2) + Р(А3) = 0,15+0,23+0,17=0,55
Р( 
Ответ: 0,45
Пример 3
Из колоды, содержащей 36 карт, наудачу вынимают три карты. Какова вероятность того, что среди них окажется хотя бы одна «дама»?
Комментарий к решению
Формулировка задачи содержит фразу «хотя бы одна», что позволяет решать ее двумя способами: на основе теоремы 1 и с использованием следствия 2. Рассмотрим оба способа решения.
Решение 1
Обозначим события: А – из трех карт хотя бы одна дама,
А1 – из трех карт одна дама А2 – из трех карт две дамы
А3 – все три карты - дамы
А = А1 + А2 + А3
Так как событияА1, А2, А3 – несовместные, по теореме 1 получим:
Р(А) = Р(А1+ А2 + А3) = Р(А1) + Р(А2) + Р(А3), где каждое слагаемое вычислим на основе формул сочетания и классической формулы вероятности.
Р(А1)=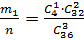 
, где
|
|
|
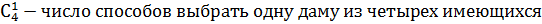
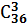– число способов выбрать три карты из колоды в 36 карт
Р(А2)=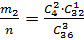 
, где
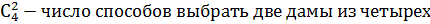
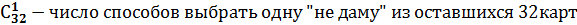
Р(А3)=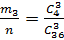 
, где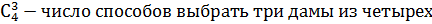 
Тогда получим:
Р(А) = Р(А1+ А2 + А3) = Р(А1) + Р(А2) + Р(А3)=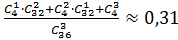 
Решение 2
Обозначим события: А – из трех карт хотя бы одна дама,
– среди трех карт нет ни одной дамы
По следствию 2 имеем: Р(А) = 1 - Р( , где
Р(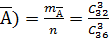 
= 
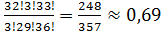
Тогда Р(А) = 1 - Р( 
Ответ: 0,31
Для произвольных событий теорема сложения вероятностей имеет другой вид.
Теорема 2. Если события А и В совместные, то вероятность их суммы равна сумме вероятностей этих событий без вероятности их совместного наступления, т.е.
Р(А+В) = Р(А) + Р(В) – Р(АВ) (6)
Замечание
Формулу (6) можно распространить на любые три события А, В и С:
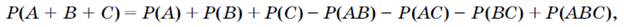
Пример 4
Числа 1,2, 3, …, 20 написаны на листах бумаги, которые помещены в коробку и тщательно перемешаны. Из коробки наугад вынимают один лист. Какова верочятность того, что число на вынутом листе окажется либо простым, либо делящимся на три?
|
|
|
Решение
Опыт: из коробки с 20 листами наугад вынимают один лист
А – на вынутом листе простое число → А = {2, 3, 5, 7, 11, 13, 17, 19}
В – на вынутом листе число, кратное 3 → В = {3, 6, 9, 12, 15, 18}
А и В – совместные, тогда по теореме 2 получим:
Р(А+В) = Р(А) + Р(В) – Р(АВ),
где АВ – на вынутом листе простое число, кратное 3 → АВ = {3}
Р(А)= 
, Р(B)=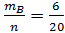 
, P(AB)=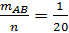 
Р(А+В) =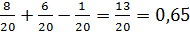 
Ответ: 0,65
Заметим, что формула (1) следует из формулы (6). Действительно, если события А и В несовместные, то их произведение является невозможным событием, поэтому Р(АВ)=0 и формула (6) превращается в формулу (1).
| 3. | Теоремы умножения вероятностей 3.1. Зависимые и независимые события |
Совместные события разделяются на зависимые и независимые. Чтобы определиться с их трактовкой рассмотрим испытания, связанные с извлечением шаров из ящика, в котором находятся три шара: белый, красный и черный. Из ящика последовательно извлекают два шара. Эти испытания можно проводить двумя способами.
|
|
|
| 1 способ | 2 способ |
| Извлекают 1й шар (1е испытание), фиксируют его цвет и кладут обратно в ящик. Шары перемешивают и извлекают второй шар (2е испытание). В этом случае результаты испытаний никак не влияют друг на друга. Такие испытания называют независимыми. | Извлекают 1й шар (1е испытание), фиксируют его цвет и кладут обратно в ящик. Шары перемешивают и извлекают второй шар (2е испытание). В этом случае результаты испытаний никак не влияют друг на друга. Такие испытания называют зависимыми |
Зависимость испытаний друг от друга приводит к зависимости событий, которые могут произойти в этих испытаниях.
Определение
Два события А и В называются независимыми, если появление одного из них не меняет вероятность появления другого. В противном случае события А и В называются зависимыми.
Примеры:
1) Опыт: двукратное подбрасывание игрального кубика
А – выпадение шести очков при 1м бросании
В – выпадение четного числа очков при 2м бросании
А и В независимые, так как Р(А)=1/6, Р(В)=3/6.
2) Опыт: последовательное извлечение двух карт из полной колоды
С – 1я вынутая карта – «туз», Р(С)=4/36, R – 2я вынутая карта – «туз» R зависит от С, так как, если событие С наступило, то Р(R)=3/35, а если событие С не случилось, то Р(В)=4/35.
Дата добавления: 2022-07-02; просмотров: 166; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!