Определитель квадратной матрицы.

Стр 1 из 3Следующая ⇒

Группа 1-ПР-21/з

Тема «ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦ»

Вид занятия: лекция

Тип занятия : усвоения новых знаний

Цель:

· изучение основные понятия теории матриц,

· алгоритмы выполнения действий над матрицами,

· алгоритм нахождения обратной матрицы;

· формирование навыков самостоятельной работы по заданному алгоритму;

· формирование умений самостоятельно пополнять знания, пользоваться учебной литературой и др. источниками.

В результате изучения темы студент должен знать:

определение матрицы, ранга матрицы, обратной матрицы,

алгоритм выполнения сложения, вычитания, умножения матрицы на число, умножение матриц, алгоритм вычисления ранга матрицы, определителя квадратной матрицы 2-го и 3-го порядков, алгоритм нахождения обратной матрицы.

В результате изучения темы студент должен уметь:

вычислять определители квадратной матрицы 2-го и 3-го порядков, по алгоритму находить матрицу, обратную к заданной матрице, выполнять действия над матрицами, вычислять ранг матрицы.

Литературные источники:

1. Богомолов Н.В. Практические занятия по математике. - М.: Дрофа - 2010.- 400 с.

2. Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. - М.-Дрофа-2009.

3. Григорьев С.Г. Математика: учебник для студентов сред. проф. учреждений / С.Г. Григорьев, С.В. Задулина; под ред. В.А. Гусева. - 2-е изд., стер. - М.: Издательский центр «Академия», 2007. - 384 с.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. - 4-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2010. - 573 с.

5. Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. - М.: Издательский центр «Академия», 2007. - 352 с.

6. Спирина М.С. Дискретная математика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. - М.: Издательский центр «Академия», 2010. - 368 с.

7. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах. Часть 1 и 2. - М.: Высшая школа, 2008.

8. Н.В. Богомолов Задачи по математике с решениями. - М.: Высшая школа, 2006

9. Н.В. Богомолов, П.И. Самойленко Математика. - М.: Дрофа, 2004

10. З.И. Гурова, С.Н. Каролинская, А.П. Осипова Математический анализ. Начальный курс с примерами и задачами- М.: ФИЗМАТЛИТ, 2002

11. И.Д. Пехлецкий Математика. - М.: Мастерство, 2001

12. В.Ф. Бутузов, Н.И. Крутицкая. Математичесий анализ в вопросах и задачах. - М.: Физматлит, 2000

1. Перечень вопросов и задач для подготовки к семестровому контролю.

1.1 Перечень вопросов для семестрового контроля (экзамен) по дисциплине ЕН.01 Математика

1. Определение матрицы. Виды матриц. Действия над матрицами.

2. Определители 2-го, 3-го порядка. Вычисление. Свойства определителей. Теорема Лапласса.

3. Обратная матрица. Алгоритм нахождения обратной матрицы.

4. Решение систем линейных уравнений методами Гаусса, Крамера, обратной матрицы.

5. Особенности канонической формы задачи линейного программирования. Симплекс-метод. Графический метод.

6. Классическая постановка транспортной задачи. Метод потенциалов.

7. Непрерывность функции. Точки разрыва, их классификации.

8. Предел функции. Раскрытие неопределенностей.

9. Комплексные числа и действия над ними. Алгебраическая, тригонометрическая и показательная форма комплексного числа.

10. Производная функции, ее механический, геометрический, экономический смысл.

11. Правила дифференцирования. Таблица производных.

12. Теоремы Ролля, Лагранжа, Коши, Ферма.

13. Экстремумы функции.

14. Выпуклость функции. Точки перегиба.

15. Исследование функции с помощью производной. Построение графиков функций.

16. Первообразная функции. Неопределенный интеграл. Таблица интегралов.

17. Интегрирование методом подстановки и по частям.

18. Определенный интеграл. Механический, экономический смысл.

19. Теорема Ньютона-Лейбница.

20. Основные понятия о дифференциальных уравнениях. Дифференциальные уравнения І порядка. Задача Коши.

УТВЕРЖДЕНО: на заседании цикловой комиссии естественно-математических дисциплин протокол № _____ от _______________ Председатель цикловой комиссии ___________________Н.А.Дулина

Подготовил Преподаватель _______ Л.И. Григорьева ____. ____. 2022 г.

1.2 Перечень типовых упражнений и задач

для семестрового контроля (экзамен) по дисциплине ЕН.01 Математика

1. Выполнение действий над матрицами: сложение, вычитание, умножение матриц, умножение матрицы на число, транспонирование.

2. Вычисление определителей 2-го, 3-го порядков. Применение теоремы Лапласса для вычисления определителя 4-го порядка.

3. Нахождение обратной матрицы.

4. Решение систем линейных уравнений методом Крамера, Гаусса, обратной матрицы.

5. Вычисление производных сложной, неявной, параметрически заданной функции.

6. Интегрирование по частям, методом подстановки.

7. Нахождение промежутков возрастания (убывания) функций, экстремумов, критических точек.

8. Нахождение промежутков выпуклости (вогнутости) графиков функций, точек перегиба.

9. Решение задач по исследованию функций на максимум (минимум).

10. Решение задач с использованием геометрического, физического, экономического смысла производной.

11. Использование механического, экономического смысла определенного интеграла при решении задач.

12. Выполнение действий над комплексными числами в алгебраической форме.

13. Решение дифференциальных уравнений І порядка. Решение задачи Коши.

Подготовил Преподаватель _______ Л.И. Григорьева ____. ____. 2022 г.

Изучение нового материала.

Основные понятия

Определение. Матрицей называется прямоугольная таблица чисел, которая имеет т строк и п столбцов. Если вернуться к системе уравнений (1.1), то коэффициенты при неизвестных в левой части как раз и образуют такую прямоугольную таблицу:

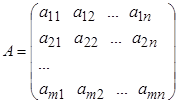
Числа аij называются элементами матрицы, а запись т × п означает ее размер. Заметим, что на первом месте в этой записи указано количество строк матрицы, а на втором - количество столбцов. Например, запись размера матрицы 5 × 3 означает, что в ней пять строк и три столбца. Если количество строк матрицы равно числу ее столбцов, то матрица называется квадратной.

Две матрицы равны между собой, если они имеют одинаковый размер и все их соответствующие элементы равны между собой.

Элементы с двумя одинаковыми индексами a₁₁, a₂₂, a₃₃, ..., a_nn образуют главную диагональ матрицы. Если а_ij = а_ji, то матрица называется симметричной.

Квадратная матрица, в которой элементы главной диагонали равны единице, а все остальные нулю, называется единичной матрицей:

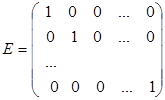
Когда все элементы матрицы, содержащиеся по одну сторону от главной диагонали, равны нулю, то матрица называется треугольной.

Каждой квадратной матрице можно поставить в соответствие определитель, который состоит из тех же элементов.

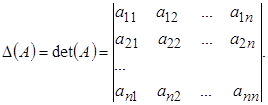
Если такой определитель отличен от нуля, то матрица называется не особенной, или невырожденной. Если определитель равен нулю, то матрица особенная, или вырожденная.

Действия над матрицами

1. Суммой матриц одного и того же порядка А = (а_ij) и В = (b_ij) называется матрица С = А + В;

С = (с_ij), любой элемент которой равен сумме соответствующих элементов матриц

А и В : c_ij = a_ij + b_ij . Например, обе матрицы ,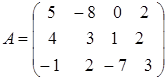

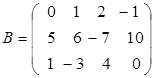имеют размер 3 х 4, поэтому по определению можно создать их сумму – матрицу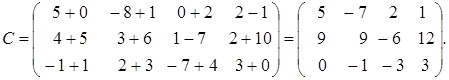

2. Произведением матрицы А = (а_ij) на некоторое число α называется такая матрица С, каждый элемент которой с_у образуется умножением соответствующих элементов матрицы А на α, с_ij= αа_ij

Пример.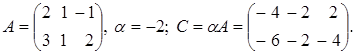

Очевидно, что для суммы матриц и произведения матриц на число выполняются равенства:

1) А + В = В + А; 2) α A = Аα;

3) α(А + В) = αА + αВ ; 4) (α + β)A = αA + βA

5) α(βА) = (αβ)А.

Произведением матрицы А = (а_ij) размера т × р на матрицу В = (b_ij) размера р × п называется такая матрица С = АВ размера т × п, С = (с_ij), каждый элемент можно найти по формуле:

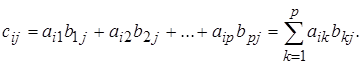
Каждый элемент матрицы С образуется как сумма произведений соответствующих элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В, то есть по схеме:

Отметим, что в результате умножения получим матрицу размера т × п.

Из определения следует, что произведение матриц некоммутативное АВ ≠ ВА.

Вернемся к системе уравнений (1.1) и образуем матрицы: А - коэффициентов при неизвестных, X- неизвестных, В - свободных членов:

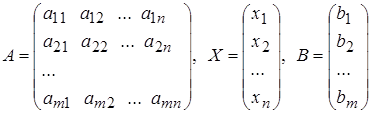
Тогда согласно определению произведения матриц систему уравнений можно записать в матричном виде:

АХ = В, (1.5)

который значительно сокращает запись системы уравнений.

Определитель квадратной матрицы.

Определитель – это число, характеризующее квадратную матрицу. Определитель обозначается знаком Δ.

Определение . Определителем квадратной матрицы n -го порядка называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца

Определение. Определителем матрицы первого порядка , т.е. матрицы состоящей из единственного элемента а_11, является сам элемент а_11.

Определение. Определитель квадратной матрицы второго порядка (размерность матрицы 2*2) равен разности произведений элементов главной диагонали и элементов побочной диагонали.

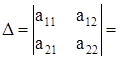а₁₁ · а₂₂ – а₁₂· а₂₁

Пример. Для матрицы 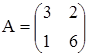вычислим определитель.

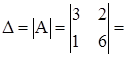3 · 6 – 1 · 2 = 18 – 2 = 16

Ответ: 16.

Определение . Определитель квадратной матрицы третьего порядка (размерность матрицы 3*3) вычисляется по правилу треугольников (или правилу Сарруса):

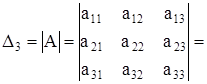а₁₁·а₂₂ ·а₃₃ + а₁₂·а₂₃ ·а₃₁ + а₂₁·а₃₂ ·а₁₃ – а₃₁·а₂₂ ·а₁₃ –

– а₁₂·а₂₁ ·а₃₃ – а₁₁·а₃₂ ·а₂₃

Схематично правило треугольников (Сарруса) можно представить в виде:

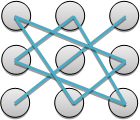произведения указанных элементов берут со знаком

« + » « – »

Для определителей квадратных матриц более высокого порядка не существует алгоритма вычисления. Определители матриц более высокого порядка вычисляются с помощью теоремы Лапласа. Так, определитель 4-го порядка можно разложить по элементам любой строки (столбца), используя определители 3-го порядка.

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Алгебраическим дополнением А_ij элемента а_ijматрицы п-го порядка называется его минор со знаком (–1)^i+j. i- номер строки и j-номер столбца.

Алгебраическое дополнение вычисляется по формуле: A_ij = (–1)^i+j · M_{ij ,}

где M_ij минор матрицы_-

Минором М_ij матрицы п-го порядка называется определитель матрицы (п-1)-го порядка, образованный из элементов заданной матрицы путем вычеркивания i-й строки и j-го столбца.

Обратная матрица

Определение. Матрица А^-1 называется обратной матрицей к квадратной невырожденной матрице А, если выполняется соотношение: АА^-1 = А^-1А = Е.

Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица существует тогда и только тогда, когда исходная матрица является невырожденной.

Матрица называется невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется вырожденной.

Пусть дана квадратная матрица. Докажем, что когда Δ (А) ≠ 0, существует обратная матрица A^-1. Рассмотрим матрицу:

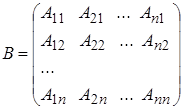Образуем произведение АВ и ВА.

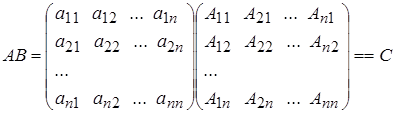
По правилу умножения матриц элементы матрицы С находим по формуле:

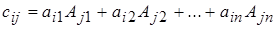
(1.6)

Если i = j, то по формуле (1.3) имеем: с_ij = Δ (А), то есть находим значение определителя матрицы А; если i ≠ j, то выражение (1.6) представляет собой сумму произведений элементов i-й строки определителя на алгебраические дополнения, соответствующие j-й строчке этого самого определителя. По свойству 9 определителей такая алгебраическая сумма равна нулю. Итак, cij = 0, если i ≠ j. Матрица С принимает вид: 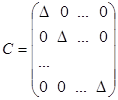. Чтобы эта матрица стала единичной, надо умножить ее на .

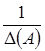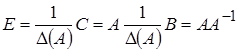
Итак, обратная матрица имеет вид:

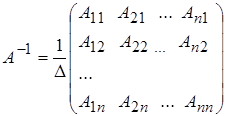
Докажем, что для матрицы А матрица А^-1 единственная. Для этого предположим обратное. Пусть существует одна матрица С, такая что АС = СА = Е. Тогда

САА^-1 = С (АА^-1) = СЕ = С,

а в то же время

САА^-1 = (СА) А^-1 = ЕА^-1 = А^-1 отсюда С = А^-1

Приходим к выводу, что первоначальное предположение неверно, то есть обратная матрица единственная.

Вернемся теперь к выражению (1.5) - записи системы уравнений в матричном виде АХ = В Предположим, что система состоит из п линейных уравнений с п неизвестными, матрица А - квадратная и Δ (A) ≠ 0 - матрица невырожденная. Тогда для матрицы А построим обратную А^-1 - она тех предположений, которые только сделано, существует. Умножив теперь матричную равенство АХ = В слева на матрицу А-1, получим:

А ^–¹ (АХ) = А ^–¹ В Þ (А ^–¹A ) X = А ^–¹В Þ ЕХ= А ^–¹ В,

либо окончательно X = А^–1 В.

Последнее выражение - это решение системы линейных уравнений. Заметим, что в таком виде можно записать решение любого матричного уравнения, если матрица А удовлетворяет условиям существования А^-1.

Ранг матрицы

Рассмотрим матрицу A размером т × п

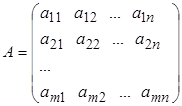
и введем еще одно важное понятие.

Определение. Рангом матрицы А размером т × п называется высокий порядок отличного от нуля минора, образованного из элементов этой матрицы. Понятно, что Rang = r ≤ min (m, п), а наибольший возможный ранг матрицы может равняться меньшему из чисел т и п.

Рассмотрим также понятие обводного минора k-го порядка. Это будет такой минор (k + 1) -го порядка, который полностью включает в себя минор k-го порядка.

Вычисляя ранг матрицы, нужно переходить от миноров меньших порядков, отличных от нуля, до миноров больших порядков. Если найдено отличный от нуля минор М k-го порядка, то достаточно вычислить только миноры (k + 1) -го порядка, обводят минор М. если все они равны нулю, то ранг матрицы равен k. Если среди них найдется отличный от нуля, то дальше для него строятся обводные миноры (k + 2) -го порядка и т. д.

Определение. Элементарными преобразованиями матрицы А называются такие ее преобразования:

- замена местами двух строк или двух столбцов матрицы;

- умножения строки или столбца матрицы на произвольное отличное от нуля число;

- добавления элементов одной строки или столбца в соответствующие элементы другой строки или столбца, предварительно умноженного на некоторое число.

Дата добавления: 2022-06-11; просмотров: 55; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!