Способы решения квадратных уравнений
3.1. Стандартные способы
Для начала повторим то, что нам уже известно. Квадратное уравнение — это алгебраическое уравнение общего вида: 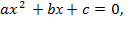 где — x свободная переменная, a,b и c — коэффициенты, причём a
где — x свободная переменная, a,b и c — коэффициенты, причём a  0 .
0 .
В школьной программе мы изучаем всего несколько различных способов решения квадратных уравнений, такие как:
1. Решение через дискриминант, 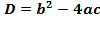 при этом:
при этом:
a) Если D > 0, то квадратное уравнение имеет два различных корня, которые находятся по формуле 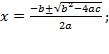
b) Если D = 0, то квадратное уравнение имеет два одинаковых корня x 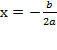 ;
;
c) Если D < 0, то действительных корней нет;
2. Решение через D 1 (в случае если коэффициент b чётный), который находится по формуле D1 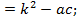 где k =
где k = 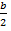 , отсюда формула нахождения корней:
, отсюда формула нахождения корней: 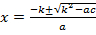 . Данный способ облегчает решение уравнения, но коэффициент b не всегда чётный;
. Данный способ облегчает решение уравнения, но коэффициент b не всегда чётный;
3. Решение через теорему Виета. Исходя из теоремы, учащиеся методом подбора могут находить корни приведённого квадратного уравнения. По теореме Виета в уравнении 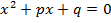 сумма корней равна его второму коэффициенту
сумма корней равна его второму коэффициенту 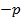 , а произведение – свободному члену q, то есть:
, а произведение – свободному члену q, то есть: 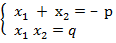 ;
;
|
|
|
4. Также учениками изучается способ выделение полного квадрата, используется он реже всего.
Теперь давайте разберём способы, облегчающие решение некоторых квадратных уравнений:
3.2. Нестандартные способы
Решени е уравнений способом «переброски».
Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. Умножая обе его части на а, получаем уравнение а2х2 + аbх + ас = 0. Пусть ах = у, откуда х = 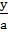 ; тогда приходим к уравнению у2 + by + ас = 0. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем: х1 =
; тогда приходим к уравнению у2 + by + ас = 0. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем: х1 = 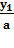 и х2 =
и х2 = 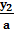 .
.
|
|
|
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, отсюда и название. Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета.
Примеры:
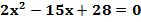
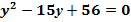 ; ;
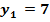 ; ; 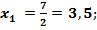
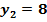 ; ; 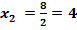 .
Ответ: 4; 3,5. .
Ответ: 4; 3,5.
| 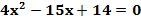 ; ;
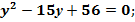 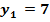 ; ; 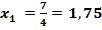 ; ;
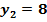 ; ; 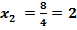 .
Ответ: 1,75; 2. .
Ответ: 1,75; 2.
|
2. 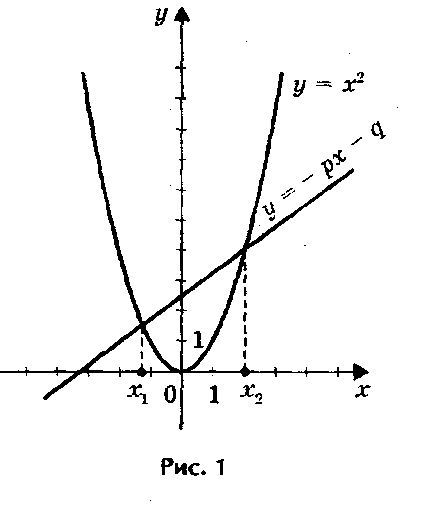 Графическое решение квадратного уравнения.
Графическое решение квадратного уравнения.
Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = - px - q .
Построим графики зависимости у = х2 и у = - px - q.
График первой зависимости - парабола, проходящая через начало координат. График второй зависимости - прямая (рис.1). Возможны следующие случаи:
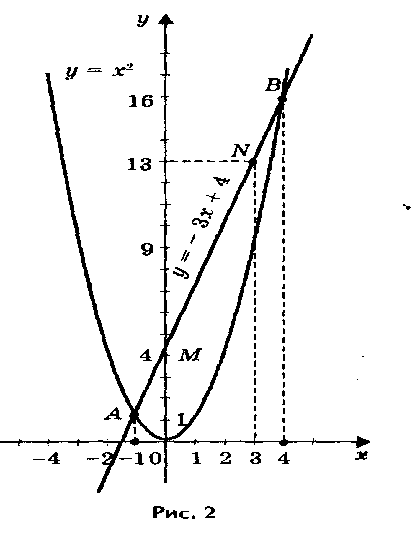 - прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут касаться (одна общая точка), т.е. уравнение имеет одно решение;
- прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
• Примеры.
|
|
|
1) Решим графически уравнение х2 - 3х - 4 = 0 (рис. 2).
 Решение. Запишем уравнение в виде х2 = 3х + 4.
Решение. Запишем уравнение в виде х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4. Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13). Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1 = - 1 и х2 = 4. Ответ: х1 = - 1; х2 = 4.
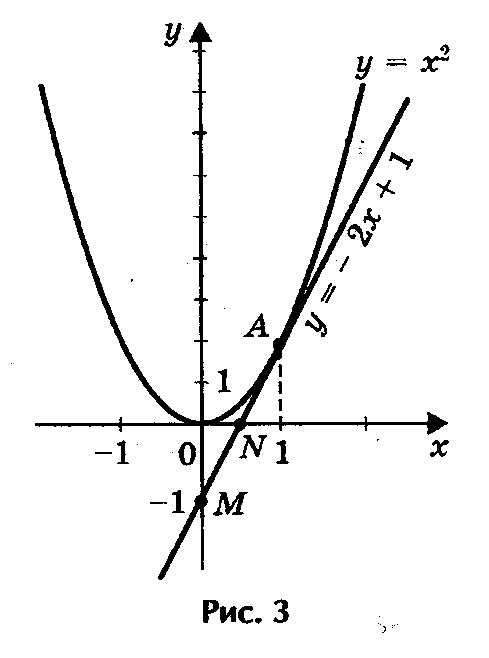
2) Решим графически уравнение (рис. 3) х2 - 2х + 1 = 0.
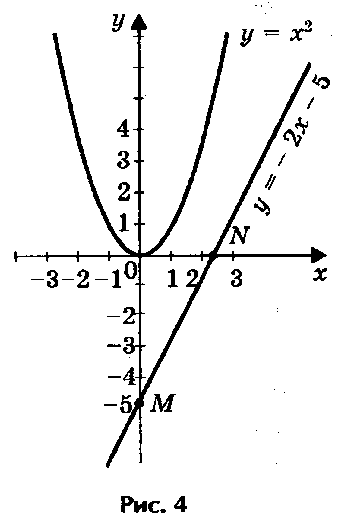 Решение. Запишем уравнение в виде х2 = 2х - 1.
Решение. Запишем уравнение в виде х2 = 2х - 1.
Построим параболу у = х2 и прямую у = 2х - 1.
Прямую у = 2х - 1 построим по двум точкам М (0; - 1)
и N (1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х2 - 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х2 = 5х - 5. Построим параболу у = х2 и прямую у = 2х - 5. Прямую у = 2х - 5 построим по двум точкам М(0; - 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 - 2х + 5 = 0 корней не имеет.
Дата добавления: 2022-06-11; просмотров: 18; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
