К в а д р а т н ы е у р а в н е н и я.

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Квадратные уравнения. Квадратное уравнение – это уравнение вида ax²+bx+c=0, где a, b, c – числа, причем a≠0, или уравнение, к нему сводящееся.

Число a называется старшим (первым) коэффициентом, число b – вторым коэффициентом, число c – свободным членом.

Замечание.

1) Заметим, что если a=0, то уравнение (3) становится линейным; именно поэтому в определении a≠0.

2) Выражение ax²+bx+c называется квадратичным (квадратным) трехчленом.

ВАЖНО! Обращаем ваше внимание на то, что, например, в квадратном трехчлене 7−x²+2x коэффициент a=−1, b=2 и c=7! Так как 7−x²+2x=−x²+2x+7, а по определению a – коэффициент перед x², b – коэффициент перед x, c – свободный член.

Определение. Дискриминантом квадратного уравнения (3) называется выражение D=b²−4ac.

Корни квадратного уравнения.

1) Если дискриминант квадратного уравнения больше нуля (D>0), то оно имеет два различных корня и x₁= 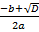и x₂= .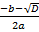

2) Если дискриминант квадратного уравнения равен нулю (D=0), то оно имеет два совпадающих корня (часто говорят, что оно имеет один корень) x=−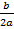

3) Если дискриминант квадратного уравнения меньше нуля (D<0), то оно не имеет корней.

Пример: Решите уравнение 3x²−33x+90=0.

Решение. Найдём дискриминант данного уравнения: D=33²−4⋅3⋅90=9. Следовательно, уравнение имеет два различных корня, равных и x₁=33+3/6=6 и x₂=33−3/6=5

Теорема Виета. Пусть квадратное уравнение ax²+bx+c=0, a≠0, имеет два корня x₁ и x₂ (возможно, совпадающих), то есть D⩾0. Тогда их сумма равна x₁+x₂=− 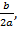а их произведение равно x₁⋅x₂=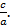

Определение. Квадратное уравнение называется приведенным, если старший коэффициент a=1. Любое квадратное уравнение можно сделать приведенным: для этого необходимо разделить уравнение на a.

Следствие. Для приведенного квадратного уравнения x²+px+q=0 теорема Виета выглядит следующим образом: x₁+x₂=−p, x₁⋅x₂=q.

Теорема: разложение на множители квадратного трехчлена.

Пусть уравнение ax²+bx+c=0, a≠0, имеет два корня (возможно, совпадающих), то есть D⩾0. Тогда при любом значении x выполнено ax²+bx+c=a(x−x₁)(x−x₂), где x₁ и x₂ – корни уравнения ax²+bx+c=0 (возможно, совпадающие).

Пример. Разложить на множители квадратный трехчлен 3x²−2x−1.

Решение. Рассмотрим уравнение 3x²−2x−1=0 и найдем его корни. D=(−2)²−4⋅3⋅(−1)=16, значит x₁=2−4/2⋅3=−1/3 и x₂=2+4/2⋅3=1 Таким образом, 3x²−2x−1=3(x−1)(x+1/3)=(x−1)(3x+1).

Домашнее задание. Решить самостоятельно следующие примеры.

1. Решить линейные уравнения:

А) 11,24х – 5, 47 = 6, 129;

Б) 5х ·4 = 12;

В) 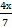– 5 = 14.

2. Решить задачу:

На первом складе было 2300м³ дров, на втором 2800м³ дров. Со второго склада взяли впятеро больше дров, чем с первого, и тогда на обоих складах дров стало поровну. Сколько дров взяли с каждого склада?

Урок. Алгебраические системы уравнений.

Перечень вопросов, рассматриваемых в теме:

1) определение алгебраической системы уравнений;

2) методы решений алгебраических систем уравнений;

3) симметрические системы уравнений.

Глоссарий по теме:

Системами уравнений называют записи, представляющие собой расположенные друг под другом уравнения, объединенные слева фигурной скобкой, которые обозначают множество всех решений уравнений, одновременно являющихся решениями каждого уравнения систем.

Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное числовое равенство, другими словами, являющаяся решением каждого уравнения системы.

Систему уравнений 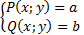называют однородной, если P(x;y), Q(x;y) — однородные многочлены одной и той же степени, а а и b — действительные числа.

Уравнение P(x;y)= а, где 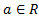, называют симметрическим, если P(х;y) — симметрический многочлен.

Систему двух уравнений с двумя переменными называют симметрической системой, если оба ее уравнения — симметрические.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Дата добавления: 2022-06-11; просмотров: 33; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!