Помехозащищенные коды. Код Грея, код с контролем паритета, код Хемминга.
Код Грея. В табл. 1.5 код Грея сопоставляется с некоторыми уже известными вам кодами. Важной особенностью кода Грея является то, что при переходе к следующему, ниже расположенному числу в предыдущем числе изменяется только одна цифра (см. правый столбец табл. 1.5). Код Грея нельзя использовать в арифметических схемах. Этот код применяется во входных и выходных устройствах цифровых систем (чаще всего для кодирования пространственного (углового) перемещения), в так называемых датчиках-энкодерах, рис. 1.11. Его использование удобно тем, что два соседних значения шкалы сигнала отличаются только в одном разряде. Также он используется для кодирования номеров дорожек в жёстких дисках. Помехозащищенность кода Грея заключается в том, что при ошибочном кодировании ошибка составляет единицу младшего разряда.
Рисунок 1.11 — Датчик-энкодер углового перемещения
Из табл. 1.1 видно, что код Грея нельзя считать одним из многочисленных вариантов двоично-десятичного кода. Заметьте также, что довольно трудно переводить десятичные числа в код Грея и переходить обратно от кода Грея к десятичным числам. Конечно, есть способы такого перевода, но обычно для этой цели используют электронные дешифраторы.
Алгоритм перехода от числа в позиционном двоичном коде к коду Грея следующий. Двоичное число надо сложить по модулю 2 (выполнить поразрядную операцию Искл-ИЛИ) с этим же числом, сдвинутым на один разряд вправо. Младший разряд при сложении не учитывается:
|
|
|
a 3 a 2 a 1 a 0
Å 0 a3 a2 a1
g 3 g 2 g 1 g 0
Пример. Преобразовать число 6 в двоичном позиционном коде в код Грея
BIN
Å 0 1 1
Gray
Алгоритм обратного перехода следующий. Старший разряд кода Грея (gi) переносится в соответствующий старший разряд числа в преобразуемом двоичном позиционном коде (ai). Для получения следующего, более младшего разряда преобразуемого позиционного кода (ai-1), соответствующий разряд в коде Грея (gi-1) складывается по модулю 2 c полученным ранее на предыдущем шаге более старшим разрядом позиционного кода (ai). Процесс повторяется до нахождения самого младшего разряда позиционного кода.
g 3 g 2 g 1 g 0
Å 0 a3 a2 a1
a3 a2 a1 a0
Пример. Преобразовать число 110 в коде Грея в двоичный позиционный код.
Gray
Å 0 1 0
BIN
Помехозащищенный код с контролем паритета. Относится к самоконтролирующимся кодам, т.е. кодам, позволяющими автоматически обнаруживать ошибочную передачу данных. Для его построения достаточно приписать к каждому слову один добавочный (контрольный) двоичный разряд и выбрать цифру этого разряда так, чтобы общее количество единиц в изображении любого числа было, например, четным. Одиночная ошибка в каком-либо разряде передаваемого слова (в том числе, может быть, и в самом контрольном разряде) изменит четность общего количества единиц. Счетчики по модулю 2, подсчитывающие количество единиц, которые содержатся среди двоичных цифр числа, могут давать сигнал о наличии ошибок.
|
|
|
При этом, разумеется, мы не получаем никаких указаний о том, в каком именно разряде произошла ошибка, и, следовательно, не имеем возможности исправить её. Остаются незамеченными также ошибки, возникающие одновременно в двух, в четырёх или вообще в четном количестве разрядов.
 k
| a6 | a5 | a4 | a3 | a2 | a1 | a0 | k | a6 | a5 | a4 | a3 | a2 | a1 | a0 | |||
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
P=1 Å 1 Å 0 Å 1 Å 1 Å 0 Å 1 Å 1=0 P=1 Å 1 Å 0 Å 1 Å 0 Å 0 Å 1 Å 1=1 Þ
Þ произошла ошибка!!!
Код Хемминга. Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для построения самокорректирующегося кода, рассчитанного на исправление одиночных ошибок, одного контрольного разряда недостаточно. Количество контрольных разрядов k должно быть выбрано так, чтобы выполнялось неравенство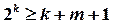 
или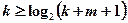 
, где m — количество основных (информационных) двоичных разрядов кодового слова. Т.е. число, кодируемое контрольными разрядами, должно описывать ( m+ k+1) различных событий, включая отсутствие ошибки (1 событие) или искажение одного из ( m+k) разрядов ( m+ k событий).
|
|
|
Таблица 1.6 Минимальные значения k при заданных значениях m для построения кода с исправлением одиночной ошибки
| Диапазон m | kmin |
| 1 | 2 |
| 2-4 | 3 |
| 5-11 | 4 |
| 12-26 | 5 |
| 27-57 | 6 |
Имея m+k разрядов, самокорректирующийся код можно построить следующим образом. Присвоим каждому из разрядов свой номер — от 1 (крайнему справа) до m+k (крайнему слева); запишем эти номера в двоичной системе счисления. Поскольку 2k>m + k , номер любого разряда можно представить, очевидно, k-разрядным двоичным числом.
Предположим далее, что все m+k разрядов кода разбиты на контрольные группы, которые частично перекрываются, причем так, что единицы в двоичном представлении номера разряда указывают на его принадлежность к определённым контрольным группам. Например: разряд №5 принадлежит к 1-ой и 3‑ей контрольным группам, потому что в двоичном представлении его номера 510 =01012 — 1-й и 3-й разряды содержат единицы.
|
|
|
Среди m+k разрядов кода при этом имеется k разрядов, каждый из которых принадлежит только к одной контрольной группе:
Разряд № 1: 110 = …000012 принадлежит только к 1-й контрольной группе.
Разряд № 2: 210 = …000102 принадлежит только к 2-й контрольной группе.
Разряд № 4: 410 = …001002 принадлежит только к 3-й контрольной группе.
…
Разряд № 2k−1 принадлежит только к k-ой контрольной группе.
Эти k разрядов мы и будем считать контрольными. Остальные m разрядов, каждый из которых принадлежит по меньшей мере к двум контрольным группам, будут информационными разрядами.
В каждой из k контрольных групп будем иметь по одному контрольному разряду. В каждый из контрольных разрядов поместим такую цифру (0 или 1), чтобы общее количество единиц в его контрольной группе было четным (табл. 1.6).
Например, довольно распространен код Хемминга с m=7 и k=4.
Пусть исходное слово (кодовое слово без контрольных разрядов) — 10101102.
Обозначим Pi — контрольный разряд №i; а Dj — информационный разряд №j, где i = 1,2,…k, j = 1,2,…m.
Предположим теперь, для примера, что при передаче данного кодового слова 10100110001 произошла ошибка в 11–м разряде, так, что было принято новое кодовое слово 0100110001. Произведя в принятом коде проверку четности внутри контрольных групп, мы обнаружили бы, что количество единиц нечетно в 1-й, 2-й и 4-й контрольных группах, и четно в 3-й контрольной группе. Это указывает, во-первых, на наличие ошибки, во-вторых, означает, что номер ошибочно принятого разряда в двоичном представлении содержит единицы на первом, втором и четвёртом местах и нуль — на третьем месте, т.к ошибка только одна, и 3-я контрольная сумма оказалась верной (табл. 1.7).
Таблица 1.6 — Формирование значений контрольных разрядов кода Хемминга
| № разряда BIN: | 1011 | 1010 | 1001 | 1000 | 0111 | 0110 | 0101 | 0100 | 0011 | 0010 | 0001 | |
| Распределение контрольных и информационных разрядов | d 7 | d6 | d5 | p4 | d4 | d3 | d2 | p3 | d1 | p2 | p1 | |
| Информационное кодовое слово: | 1 | 0 | 1 | 0 | 1 | 1 | 0 | |||||
| Вычисление | p1 | 1 | 1 | 0 | 1 | 0 | 1 | |||||
| p2 | 1 | 0 | 0 | 1 | 0 | 0 | ||||||
| p3 | 0 | 1 | 1 | 0 | ||||||||
| p4 | 1 | 0 | 1 | 0 | ||||||||
| Кодовое слово с контрольными разрядами: | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |
Таблица 1.7 — Проверка контрольных сумм на приемной стороне
| № разряда: | 1011 | 1010 | 1001 | 1000 | 0111 | 0110 | 0101 | 0100 | 0011 | 0010 | 0001 | ||
| Распределение контрольных и информационных разрядов | d7 | d6 | d5 | p4 | d4 | d3 | d2 | p3 | d1 | p2 | p1 | Контроль по четности в группе | Контрольный бит |
| Переданное кодовое слово: | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | ||
| Принятое кодовое слово: | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | ||
| p1 | 0 | 1 | 0 | 1 | 0 | 1 | Fail | 1 | |||||
| p2 | 0 | 0 | 0 | 1 | 0 | 0 | Fail | 1 | |||||
| p3 | 0 | 1 | 1 | 0 | Pass | 0 | |||||||
| p4 | 0 | 0 | 1 | 0 | Fail | 1 |
p4 p3 p2 p1
В двоичном представлении 1 0 1 1
В десятичном представлении 8+2+1=11
Из таблицы следует, что ошибка произошла в 11-м разряде и её можно исправить (проинвертировав принятый 11-ый разряд d7). Построенный код, разумеется, не рассчитан на возможность одновременной ошибки в двух разрядах.
1.10 Компьютерные форматы данных
Успешное программирование требует полного понимания форматов данных. Обычно данные представляются в микрокомпьютерной системе в следующих основных видах: формате ASCII, как двоично-кодированные десятичные числа (BCD), целые числа со знаком и без, а также иногда как числа с плавающей точкой (действительные числа). Могут быть использованы и другие формы представления данных, однако они здесь не описываются, поскольку не являются столь же широко распространенными.
Дата добавления: 2022-01-22; просмотров: 84; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!