Двоично-десятичные ( BCD) коды. BCD коды самодополняющиеся и несамодополняющиеся.
М.А. АМЕЛИНА
e-mail: amelina.marina@gmail.com
Конспект лекций
По курсу
«Цифровая техника»
Курс
Семестр
2013
Оглавление
СПИСОК СОКРАЩЕНИЙ.. 3
1 Логические основы цифровых устройств.. 4
1.1 Общие сведения о цифровых устройствах. 4
1.2 Алгебра логики. 6
1.3 Основные логические операции и способы их аппаратной реализации. 8
1.4 Универсальные логические операции и их особенности. 11
1.5 Формы записи логических функций (ДНФ, КНФ) 12
1.6 Переход от логической функции к логической схеме. 13
1.7 Минимизация логических функций. 14
1.8 Запись и реализация логических функций в универсальных базисах. 17
1.9 Коды и системы счисления. 19
1.10 Компьютерные форматы данных. 26
2 Элементы цифровых устройств.. 33
2.1 Комбинационные и последовательностные устройства. 33
2.2 Шифраторы, дешифраторы, преобразователи кодов. 35
2.3 Мультиплексоры и демультиплексоры.. 38
2.4 Компараторы кодов. 41
2.5 Двоичные полусумматор и сумматор. 42
2.6 Арифметико-логические устройства. 47
2.7 Триггеры.. 50
2.8 Счетчики. 60
2.8.1 Основные параметры и классификация счетчиков. 60
2.8.2 Двоичные счетчики. 61
2.8.3 Двоично-кодированные счетчики. 73
2.8.4 Счетчики с недвоичным кодированием состояний. 80
2.9 Регистры и регистровые файлы.. 91
2.9.1 Параллельные регистры.. 91
2.9.2 Регистровые файлы.. 92
2.9.3 Сдвигающие регистры.. 94
2.9.4 Универсальные регистры.. 96
2.10 Запоминающие устройства. 100
3 СИНТЕЗ ЦИФРОВЫХ АВТОМАТОВ.. 101
|
|
|
3.1 Синтез асинхронных автоматов на RS-триггерах. 101
3.1.1 Пример 1. 101
3.1.2 Пример 2. 103
3.1.3 Пример 3 — Автомат Мили. 105
3.1.4 Пример 4 — автомат Мура. 107
3.2 Синтез асинхронных автоматов на мультиплексорах. 110
3.2.1 Пример 1. Асинхронный автомат Мили. 110
3.2.2 Пример 2. Асинхронный автомат Мура. 112
3.3 Синтез синхронных автоматов. 115
3.3.1 Пример 3. Синтез счетчика с изменяемым коэффициентом пересчёта. 115
ЛИТЕРАТУРА.. 118
СПИСОК СОКРАЩЕНИЙ
АЛУ — арифметическо-логическое устройство
ASCII — Американский Стандартный Код для Информационного Обмена (American Standard Code for Information Interchange)
БИС — большая интегральная схема
ГТИ — генератор тактовых импульсов
ИМС — интегральная микросхема
ЛЭ — логический элемент
МПС — микропроцессорная система
ОЗУ — оперативное запоминающее устройство
ПЗУ — постоянное запоминающее устройство
ПЛМ — программируемая логическая матрица
СБИС — сверхбольшая интегральная схема
СДНФ — совершенная дизъюнктивно-нормальная форма записи логических выражений
СИ — синхроимпульс
СКНФ — совершенная конъюнктивно-нормальная форма записи логических выражений
УГО — условное графическое обозначение
ФАЛ — функция алгебры логики
1 Логические основы цифровых устройств
|
|
|
1.1 Общие сведения о цифровых устройствах
Цифровыми называют устройства, предназначенные для формирования, преобразования и передачи кодовых слов. При этом кодовые слова (коды или числа) в электронных цифровых устройствах представляются в виде последовательностей электрических импульсов (сигналов с двумя уровнями напряжения: высоким и низким), а их преобразования осуществляются арифметическими, логическими, запоминающими и вспомогательными устройствами.
Элементами и узлами цифровых устройств, служащими основой для построения микропроцессоров, микропроцессорных систем, компьютеров, автоматизированных систем управления объектами, технологическими процессами и информационными потоками являются: дешифраторы, шифраторы, мультиплексоры, сумматоры, триггеры, регистры, счетчики и многие другие.
В современных устройствах цифровой обработки информации используется два класса переменных: числа и логические переменные. Числа несут информацию о количественных характеристиках процесса, объекта, системы, над ними можно производить арифметические действия. Логические переменные определяют состояние системы или принадлежность её к определенному классу состояний.
|
|
|
Главная особенность цифровых устройств (по отношению к аналоговым и импульсным устройствам) состоит в том, что объектами информации являются двоичные числа (кодовые слова) и логические переменные, а не непрерывные функции времени. И числа, и логические переменные могут принимать конечное множество значений, в отличие от обычных аналоговых сигналов — непрерывных функций времени.
Числа и логические переменные связаны друг с другом при решении задач управления и обработки информации. В вычислительных задачах вначале определяются совокупность и значения входных воздействий на объект управления. Предполагается, что существует математическая модель объекта в виде набора формул, таблиц, графиков и несколько логических условий. При решении задач необходимо вести анализ логических условий с выдачей логических команд. Для решения таких задач необходим специальный математический аппарат и соответствующие устройства (микропроцессоры, микроконтроллеры).
Устройство на цифровой элементной базе, выполняющее арифметические и логические операции называют арифметико-логическим устройством (АЛУ).
АЛУ, выполняющее также функции управления — центральным процессором.
|
|
|
Арифметические устройства (сумматоры, умножители) предназначены для выполнения арифметических операций над бинарными кодовыми словами.
Логическими устройствами называют схемные элементы, с помощью которых осуществляется преобразование поступающих на их входы двоичных (бинарных) сигналов и непосредственное выполнение предусмотренных логических операций.
Запоминающими называют такие устройства, которые обладают свойствами длительно сохранять поступающую в них информацию без изменения её содержания и отправлять её по команде в другие устройства.
Вспомогательными являются все прочие устройства, предназначенные для образования надёжных связей между арифметико-логическими и запоминающими функциональными узлами и внешними устройствами. К ним относят тактовые генераторы, устройства приёма и распределения данных, таймеры, усилители, повторители, инверторы и др.
Функционирование цифровых (в том числе и микропроцессорных) устройств можно представить следующим образом:
· посредством генератора тактовых импульсов производится синхронизация начала выполнения отдельных операций преобразования входного кодового слова и отводится время для выполнения команды (в течение одного или нескольких периодов тактовых импульсов);
· после активизации начала операции осуществляется преобразование всех входных кодовых слов (состоящих из логических нулей и единиц) в требуемые выходные кодовые слова;
· выходные кодовые слова отправляются на хранение в память цифрового устройства и/или во внешние устройства для выполнения определенных действий.
Операции над кодовыми словами, представленными в виде электрических сигналов, в цифровом устройстве могут выполняться следующими двумя способами:
1) Последовательное (поразрядное, побитовое) выполнение операций, при котором символы 1 и 0 кодового слова поступают последовательно по времени на единственный вход цифрового устройства и по завершении операции последовательно символ за символом выводятся из него. На рис. 1.1, а показано выполнение операции цифровым устройством ЦУ (инвертором) над трехразрядным входным словом x2x1x0=100, при котором биты выходного слова у2y1y0=011 принимают противоположные значения;
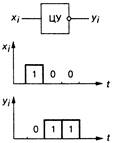
а б
в г
Рисунок 1.1 — Способы выполнения операций в цифровых устройствах
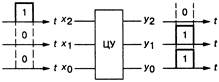
2) Параллельное выполнение операций, при котором символы 1 и 0 кодового слова поступают одновременно на три входа ЦУ и по завершении операции одновременно выводятся из него (рис. 1.1, б).
В рассмотренных устройствах для выполнения операций над кодовыми словами использовались устройства последовательного и параллельного действия, а входные и выходные слова представлялись в виде последовательного и параллельного кодов.
3) В ряде случаев используют комбинированные способы обработки информации: с последовательным вводом и параллельным выводом (рис. 1.1, в) и с параллельным вводом и последовательным выводом (рис. 1.1, г).
1.2 Алгебра логики
Работа любого логического устройства подчиняется законам формальной логики, которые не допускают уклончивых ответов. Решение логических задач осуществляется с помощью логических элементов, базирующихся на математическом аппарате алгебры логики (булевой алгебры, разработанной английским математиком Джорджем Булем (1815-1864), в которой все переменные величины (и аргументы, и функции) могут принимать только два логических значения: «1» (логическая единица) и «0» (логический ноль). Во многих случаях эти символы простейшего алфавита, состоящего из двух букв, отождествляют с арабскими цифрами 1 и 0, не вкладывая в них смысла количества.
Понятия "1" и "0" являются условными, символизирующими состояния, например, релейного устройства: "включено", "выключено", высказывания «истинные» или «ложные». Как отмечалось, в цифровых электронных устройствах применяют сигналы двух уровней напряжения: низкого и высокого.
Логика называется положительной, если высокий потенциал отображает единицу, а низкий, – ноль. Если наоборот, высокий потенциал отображает ноль, а низкий, – единицу, то логика называется отрицательной. Данное правило называют логическим соглашением. Далее будет использоваться способ кодирования, называемый соглашением положительной логики.
В общем случае логическое устройство может иметь n входов и m выходов. Рассматривая входные сигналы х1, х 2 , ... , хn в качестве аргументов, можно соответствующие выходные сигналы представлять в виде функций уi =f (х 0 , х1, x 2 , ..., хn) с помощью элементарных операций алгебры логики.
Функции алгебры логики (ФАЛ), иногда называемые переключательными функциями, представляют в нескольких формах:
· в алгебраической (в виде математического выражения):
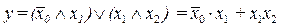Ù , × – операция «И»; Ú , + – операция «ИЛИ», 
— инверсия;
· в виде таблиц истинности или комбинационных таблиц;
· в виде временных диаграмм;
· встречается также абстрактный вид записи функций алгебры логики: у=(2, 6, 7), где в скобках приведены десятичные эквиваленты, например 3-разрядных двоичных кодовых слов, которые соответствуют значениям функции у=1 (табл. 1.1).
Таблица содержит всевозможные комбинации (наборы) бинарных значений входных переменных с соответствующими им бинарными значениями выходных переменных; каждому набору входных сигналов соответствует определенное значение выходной логической функции, (таблица 1.1). Максимальное число возможных различных наборов (строк) зависит от числа входных переменных n и равно 2 n;
Таблица 1.1 Представление логической функции в виде таблицы истинности
| x2 | x1 | x0 | y1 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| • | • | • | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
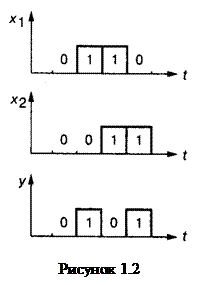На рис. 1.2 изображена временная диаграмма логической операции сложения двух кодовых слов по модулю 2:
.
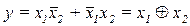Практическим препятствием для повсеместного использования табличной формы задания логических функций является быстрый рост числа строк таблицы.
При n=1 входной сигнал х может принимать лишь два значения 0 и 1. Вполне возможно, что для обоих значений х (1 и 0) выходной сигнал у может принимать значение, равное 0; в другом случае у равен 1 при х = 0 и при х=1 и т.д., т.е. цифровое устройство с одним выходом способно сформировать четыре различных варианта выходного сигнала, которые приведены в таблице 1.2.
Таблица 1.2. Варианты функций одной логической переменной
| Комбинация вх. x | 0, 1 | 0, 1 | 0, 1 | 0, 1 |
| Значение вых. функции у | 0 | 1 | 0, 1 | 1, 0 |
| Название операции | Постоянный 0 | Постоянная 1 | Повтор x | Инверсия х |
Для цифрового устройства с двумя входными переменными х1 и х 2 (n=2) возможно четыре варианта комбинаций аргументов (входных слов): 00, 01, 10 и 11 и шестнадцать различных выходных функций у i, (таблица 1.3).
В учебных примерах (как правило) ограничиваются рассмотрением логических функций двух-четырех аргументов.
Название и обозначение функции y, в какой-то мере отображает особенности выполнения логических операций (см. последнюю строку таблицы 1.3). Нулевая у0 и единичная у15 функции тривиальны, функции у3, у 5, у1 0 и у 12 не зависят от одного из аргументов: y3 = х 2, у 5 = х 1, 
, и 
. И только оставшиеся 10 функций являются функциями двух переменных.
Отметим, что многие функции имеют несколько названий. Например, логическая операция неравнозначности для функции у6 имеет название «исключающее ИЛИ», «сложение по модулю 2»; функция у7 имеет название «сложение», «дизъюнкция», «ИЛИ». Для обозначения операций логических функций используются специальные символы. Например, в качестве знака операции ИЛИ-НЕ используется символ "¯" (стрелка Пирса), условное обозначение функции у8= х 1¯ х 2; для операции И-НЕ принят символ "|" (штрих Шеффера), обозначение функции у 14= х1|х 2; для операции неравнозначности — символ Å (сложения по модулю 2), обозначение функции у6= х1 Å х 2 и т. д.
Таблица 1.3 Перечень всевозможных функций для логического устройства с двумя входами и одним выходом
|
| Значение выходной функции yi для всех комбинаций вх. сигналов | ||||||||||||||||
| Комбинации входных сигналов x2, x1 | 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 01 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 10 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 11 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
|
| y0=0 | y1=x2 × x1 | y2= x2 × x1 | y3= x2 | y4= x2 × x1 | y5= x 1 | y6= y4= x2 × x1 + x2 × x1 | y7= x2 + x1 | y8= x2 + x1 | y9= x2 × x1 + x2 × x1 | y10= x 1 | y11= x2 + x1 | y12= x2 | y13= x2 + x1 | y14= x2 × x1 | y15=1 | |
| Название функции | Постоянный 0 | Умножение, конъюнкция, И | Запрет по x1 | Тождественность x2 | Запрет по x 2 | Тождественность x 1 | Неравнозначность | Сложение, дизъюнкция, ИЛИ | Стрелка Пирса, ИЛИ-НЕ | Равнозначность | Инверсия x1, НЕ | Импликация от x 1 к × x 2 | Инверсия x 2, НЕ | Импликация от x 2 к × x 1 | Штрих Шеффера, И-НЕ | Постоянная 1 | |
|
|
AND &
Ù
|
| x2 
|
| x1
|
XOR
Å
|
OR
Ú
+
|
NOR
¯
|
XNOR
| x1
NOT
|
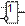
| x2
NOT
|
|
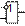
NAND
ç
| |||
1.3 Основные логические операции и способы их аппаратной реализации
В булевой алгебре выделяют три основные функции: конъюнкция, дизъюнкция, от рицание. Остальные функции являются производными от приведенных выше.
Основные логические операции состоят из следующих элементарных преобразований двоичных сигналов:
· логическое сложение или дизъюнкция (от английского "disjunction" — разъединение), обозначаемое символом "Ú" и называемое также операцией ИЛИ. При этом число аргументов (слагаемых х) может быть любым. Эта операция для функции двух переменных х 1 и х 2 описывается в виде логической формулы:
у = x1 Ú х 2 (1.1)
Запись (1.1) формулируется следующим образом: у равен х1 ИЛИ х 2. Это значит, что у истинно (равно 1), если истинно хотя бы одно из слагаемых х1 или х 2. И только в случае, когда все слагаемые х равны 0, результат логического сложения у также равен 0.
Для удобства записи сложных логических функций символ дизъюнкции "Ú" можно условно отождествлять со знаком обычного сложения "+". Для функции двух переменных:
y = x1 Ú x 2 = x1 + x 2.
Условное обозначение, таблица истинности и другие показатели этой логической функции приведены в 8-ом столбце (функция y7) таблицы 1.3;
· логическое умножение или конъюнкция (от английского слова "conjunction" — соединение), обозначаемое символом "Ù" и называемое также операцией И. При этом число аргументов (сомножителей х) может быть любым. Эта операция для функции двух переменных x 1 и х 2 описывается в виде логической формулы:
у= x1 Ù x 2 (1.2).
Запись (1.2) формулируется следующим образом: у равен х1 И х 2. Это значит, что у истинно (равно 1), если истинны оба сомножителя x1 и х 2. В случае если хотя бы один из сомножителей равен 0, результат логического умножения у тоже равен 0.
Для удобства записи сложных логических функций символ конъюнкции Ù можно условно отождествлять со знаком обычного умножения «×». Для функции двух переменных в этом случае:
y =x 1 Ù x 2 = x 1 ×x 2 .
Условное обозначение, таблица истинности логической функции И приведены во втором столбце таблицы 1.3 (функция y1).
· логическое отрицание или инверсия, обозначаемое чёрточкой над переменной и называемое операцией "НЕ". Формулируется так: у равен НЕ х. Это значит, что у истинно (равно 1), если х ложно (равно 0), и наоборот. Операция у выполняется над одной переменной х и её значение всегда противоположно этой переменной (см. 11-ый и 13-й столбцы таблицы 1.3, функции y10, y12). Операция записывается в виде:
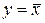(1.3)
Основные логические операции ИЛИ, И и НЕ и цифровые элементы их выполняющие (дизъюнктор, конъюнктор, инвертор) позволяют реализовать цифровое устройство без памяти, называемое комбинационным, любой степени сложности.
Примеры контактной и простейшей схемной реализаций дизъюнктора, конъюнктора и инвертора приведены на рис. 1.3.
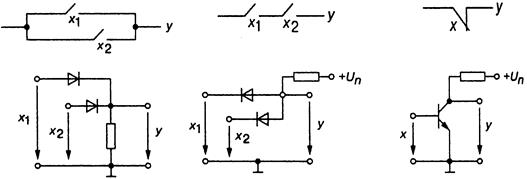
а б в
Рисунок 1.3 — Примеры контактной и простейшей схемной реализаций: а – дизъюнктора,
б — конъюнктора, в — инвертора
Сопоставляя таблицы истинности для операций «ИЛИ» и «И» (см. таблицу 1.3), можно получить некоторые соотношения булевой алгебры, имеющие большое практическое значение. Например, принцип дуальности (двойственности) булевой алгебры записывается в виде двух следующих положений:
если x1 х 2 = у, то 
(1.4)
если x1+ x 2 = у, то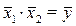 
(1.5)
Из этих соотношений вытекает теорема (правило) де Моргана: инверсия выраже ния может быть представлена тем же выражением без инверсии с изменением всех зна ков конъюнкции на знаки дизъюнкции, знаков дизъюнкции на знаки конъюнкции и инвер сией всех аргументов, т. е.
; 
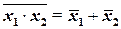(1.6)
Эти соотношения позволяют взаимно заменять операции дизъюнкции и конъюнкции, а это даёт возможность построить любую переключательную функцию, используя только две операции: «И» и «НЕ» или «ИЛИ» и «НЕ». Однако при использовании только двух элементов не всегда удается получить логические устройства наипростейшего типа. Поэтому в логических схемах находят применение и другие типовые элементы, реализующие иные логические операции, приведенные в таблице 1.3.
Приведем основные аксиомы и теоремы алгебры логики (без вывода):
Коммутативный закон:
(1.7)
Ассоциативный закон:
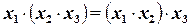
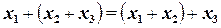(1.8)
Дистрибутивный закон:
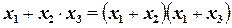(1.9)
Правило поглощения:
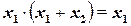
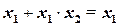(1.10)
Правило склеивания:
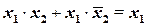
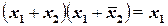(1.11)
Правило повторения:
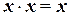
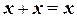(1.12)
Правило отрицания:
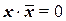
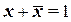(1.13)
Правило двойного отрицания:
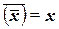(1.14)
Операции с 0 и 1:
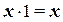
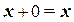(1.15)
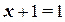
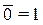
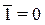
Формулы (1.12...1.15) представляют собой тождества, в справедливости которых легко убедиться прямой подстановкой х=0 и х=1. В преобразованиях логических выражений важную роль играют формулы (1.6, 1.9... 1.11), . Формулы де Моргана (1.6), как отмечалось, используют для того, чтобы перейти от логического произведения к логической сумме и обратно.
При использовании приведенных соотношений можно упростить записи и минимизировать логические выражения в смысле уменьшения числа символов.
Приведём несколько примеров.
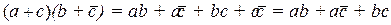
Здесь использованы тождества 
, 
, 
.
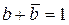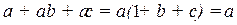
1.4 Универсальные логические операции и их особенности
Особое значение в цифровой электронике имеют универсальные (базовые) логические элементы, способные образовать функционально полный набор, с помощью которых можно реализовать все другие элементы логических базисов. В интегральной технологии удобство изготовления одного базового элемента имеет решающее значение. Поэтому базовые логические устройства составляют основу большинства цифровых ИМС. К универсальным логическим операциям (устройствам) относят две разновидности базовых элементов:
· функцию Пирса, обозначаемую символически вертикальной стрелкой ¯ (стрелка Пирса) и отображающую операцию ИЛИ-НЕ. Этой операции соответствует столбец у 8 в таблице 1.3. Для простейшей функции двух переменных x1 и х 2 функция у=1 тогда и только тогда, когда х1 = х 2=0:
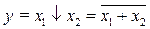(1.16)
· функцию Шеффера, обозначаемую символически вертикальной черточкой ç(штрих Шеффера) и отображающую операцию И-НЕ. Этой операции соответствует столбец у14 в таблице 1.3. Для простейшей функции двух переменных x1 и x2 функция у=0 тогда и только тогда, когда х 1 = х 2=1:
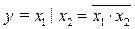(1.17)
Для построения двухвходовой схемы ИЛИ-НЕ (рис. 1.4, а) к нагрузочному резистору подключены коллекторы двух параллельно включенных биполярных транзисторов n-р-n-типа, эмиттеры которых заземлены, а для построения схемы И-НЕ на два входа потребовалось последовательное (ярусное) включение двух биполярных транзисторов n-р-n типа (эмиттер нижнего транзистора подключен к земле) и нагрузочный резистор R.
Рисунок 1.4 — Примеры контактной и простейшей схемной реализаций:
а – элемента ИЛИ-НЕ; б – элемента И-НЕ
1.5 Формы записи логических функций (ДНФ, КНФ)
Наиболее распространенным способом задания логических функций является табличная форма. Таблицы истинности позволяют полно и однозначно установить все существующие логические связи.
При табличном представлении логических функций их записывают в одной из канонических форм: совершенной дизъюнктивной нормальной форме (СДНФ) или совершенной конъюнктивной нормальной форме (СКНФ).
Математическое выражение логической функции в СДНФ получают из таблицы истинности следующим образом: для каждого набора аргументов, при котором функция равна 1, записывают элементарные произведения переменных, причем переменные, значения которых равны нулю, записывают с инверсией. Полученные произведения, называемые конституентами единицы или минтермами, суммируют.
Запишем логическую функцию у трех переменных а, b и с, представленной в виде таблицы 1.4, в СДНФ:
Таблица 1.4 — Таблица истинности функции 3-х переменных
| № | а | b | с | y |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
Для сокращения записи СДНФ представляют последовательностью номеров (десятичных чисел) конституент единицы:
у(а,b,с)=S(2,3,5,7).
Совершенной конъюнктивной нормальной формой (СКНФ) называют логическое произведение элементарных сумм, в каждую из которых аргумент или его отрицание входят один раз. При этом для каждого набора аргументов таблицы истинности, при котором функция у равна 0, составляют элементарную сумму, причем переменные, значение которых равно 1, записывают с отрицанием. Полученные суммы, называемые конституентами нуля или макстермами, объединяют операцией логического умножения. Для функции (таблица 1.4) СКНФ:
.
Для сокращения записи СКНФ представляют последовательностью номеров (десятичных чисел) конституент нуля:
у(а,b,с)=P(0,1,4,6).
1.6 Переход от логической функции к логической схеме
Для построения логической схемы необходимо логические элементы, предназначенные для выполнения логических операций, располагать, начиная от входа, в порядке, указанном в булевом выражении.
Построим структуру логического устройства, реализующего логическую функцию трех переменных, заданную таблицей истинности 1.4:
.
Слева располагаем входы a, b и с с ответвлениями на три инвертора, затем четыре элемента ИЛИ и, наконец, элемент И на выходе (рис. 1.5).
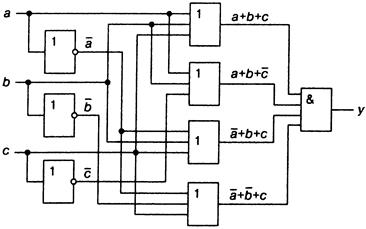
Рисунок 1.5 — Реализация логической функции, заданной табл. 1.4
Итак, любую логическую функцию можно реализовать непосредственно по выражениям, представленным в виде СДНФ или СКНФ. Однако, полученная таким образом схема, как правило, не оптимальна с точки зрения её практической реализации: она громоздка, содержит много элементов, и возникают трудности в обеспечении её высокой надёжности.
Можно минимизировать выражение для этой функции, записанное, например в форме СДНФ, используя теоремы алгебры логики:
(1.18)
1.7 Минимизация логических функций
О необходимости минимизации структурных формул СДНФ и СКНФ. Структурные формулы в виде логических функций в СДНФ и СКНФ однозначно определяют структуру логической схемы комбинационного устройства. Однако непосредственное их использование, как правило, не позволяет построить устройство, наиболее полно удовлетворяющее заданным требованиям. Недостаток построения схем комбинационных устройств по структурным формулам в СДНФ и СКНФ проявляется в том, что чаще всего устройства содержат большое количество логических элементов, имеют низкие экономические показатели и надежность. Путем тождественных преобразований структурной формулы, приводящих только к изменению ее формы, а не значений, можно значительно упростить схему комбинационного устройства (см. соотношение 1.18).
Преобразование структурной формулы с целью упрощения комбинационного устройства называется ее минимизацией. Критерием минимизации может служить число операций над переменными логической функции или логических элементов, реализующих эти операции.
Следует отметить, что критерии, в соответствии с которыми на практике осуществляют минимизацию логической функции, неоднозначны. Это минимизация стоимости её технической реализации, уменьшение количества элементарных логических элементов, использование только однородных базовых элементов, например, типа И-НЕ (ИЛИ-НЕ) и др.
Для интерпретации любых логических функций и их наглядной минимизации широко используют карты Карно-Вейча, базирующиеся на табличном представлении логических функций с числом переменных, не превышающих 4...5.
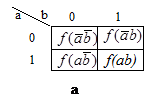
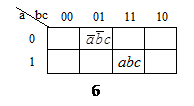
Рисунок 1.6. Изображения карт Карно для функций: а — 2-х переменных; б — 3-х переменных, в — 4-х переменных
Карта Карно — графическое представление всех возможных минтермов (2n) для данного числа переменных (n). Каждый минтерм изображается в виде клетки, расположенной так, что минтермы, соответствующие соседним клеткам, отличаются друг от друга только одной переменной. На рис. 1.6 представлены изображения карт Карно для функций двух, трех и четырех переменных. Карта для двух переменных содержит четыре клетки (рис. 1.6, а), для трех — восемь (рис. 1.6, б), для четырех — шестнадцать (рис. 1.6, в). Множество клеток позволяет отобразить все наборы аргументов, а карту Карно можно рассматривать как упорядоченное представление подмножеств. Так, на рис. 1.6, б, в нижней строке и в третьем столбце имеем пересечение аргументов a, b и с, в верхней строке и втором столбце пересечение аргументов 
, 
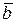и с и т. д.
Если требуется представить на карте Карно логическую функцию, заданную в виде СДНФ, то в соответствии с необходимым значением функции ставятся в надлежащих клетках 1. Остальные клетки остаются незаполненными (если для соответствующей комбинации аргументов не задано значение функции) или заполняются нулями.
Итак, логическая функция в СДНФ на карте Карно представляется совокупностью клеток, заполненных единицами, а инверсия функции представляется совокупностью пустых клеток или заполненных нулями.
На рис. 1.6, в изображена карта Карно полностью определенной логической функции в СДНФ
.
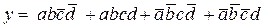Как отмечалось, для минимизации логической функции применяют метод последовательного исключения переменных с помощью законов и тождеств алгебры логики, минимизационных карт Карно и др.
Основу минимизации логических функций с помощью карт Карно составляет следующее: два минтерма, находящиеся в соседних клетках карты, могут быть заме нены одной конъюнкцией, содержащей на одну переменную меньше. Если соседними являются две пары минтермов, то такая группа из четырех соседних минтермов может быть заменена конъюнкцией, которая содержит на две переменные меньше.
При минимизации функции следует помнить, что одна и та же клетка карты Карно может входить в несколько групп и что соседними клетками являются не только клетки, расположенные рядом по горизонтали и вертикали, но и клетки на противо положных границах карты Карно.
На рис. 1.7 приведены примеры минимизации логических функций трех (а) и четырех (б) переменных.
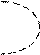
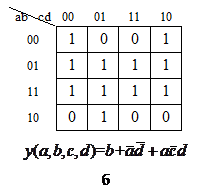
Рисунок 1.7 — Примеры минимизации логических функций: а — 3-х переменных;
б — 4-х переменных
Минимизацию ФАЛ можно проводить и с использованием нулевых значений функции. Так, для ФАЛ, представленной на рис. 1.7, а, 
, а для функции, представленной на рис. 1.7, б,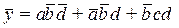 
.
Таким образом, объединение областей карты Карно по единичным и нулевым значениям функции приводит к равносильным, но различным минимальным выражениям. Следовательно, может отличаться и схема, реализующая заданный алгоритм. Поэтому для получения минимально простой технической реализации целесообразно проводить минимизацию как единичных, так и нулевых значений функции, и из полученных минимальных форм выбрать простейшую.
На практике часто встречаются логические функции, часть значений которых не задана, т. е. эти значения могут быть произвольными. Такие ФАЛ называют недоопределенными. При различном доопределении ФАЛ и минимизации по единичным и нулевым значениям функции, могут быть получены различные минимальные формы. При доопределении ФАЛ необходимо стремиться к тому, чтобы на карте Карно было выделено минимальное число максимально больших областей.
На рис. 1.8 приведены примеры доопределения ФАЛ, приводящие к получению наиболее простой реализации заданного алгоритма.
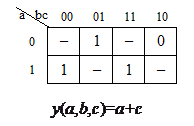
а
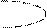
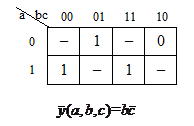
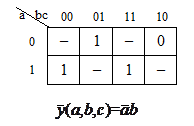
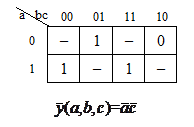
б
Рисунок 1.8 — Доопределение ФАЛ: а — единицами; б — нулями
1.8 Запись и реализация логических функций в универсальных базисах
Запись логических функций в универсальных базисах ИЛИ-НЕ и И-НЕ производится в такой последовательности:
· заданная логическая функция минимизируется в базисе ИЛИ, И, НЕ;
· над полученным выражением логической функции ставят двойное отрицание и с помощью правила де Моргана осуществляют переход в универсальный базис ИЛИ-НЕ или И-НЕ;
· при преобразовании логической функции используют следующие выражения:
в базисе И-НЕ преобразование выражения 
:
;
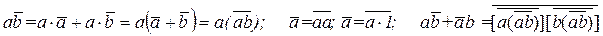в базисе ИЛИ-НЕ преобразование выражения :
.
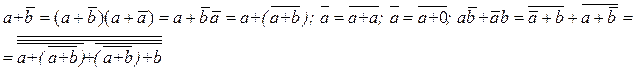При построении функциональных схем на элементах Шеффера (ИЛИ-НЕ) логическую функцию представляют в минимальной КНФ, а при построении функциональных схем на элементах Пирса (И-НЕ) — в минимальной ДНФ. В этих случаях функциональные схемы содержат минимальное количество элементов и более просты при построении.
Пример. Запишем логическую функцию 
в базисе И-НЕ и ИЛИ-НЕ в минимальных ДНФ и КНФ.
Вычерчиваем карту Карно для четырех переменных a, b, c и d (рис. 1.9) и отметим в ней единицей (1) минтермы, содержащие конъюнкции, входящие в заданную функцию. В результате склеивания минтермов в карте Карно, для которых заданная функция у=1, получим выражение для выходной функции в минимальной ДНФ:
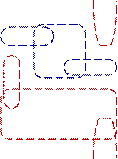
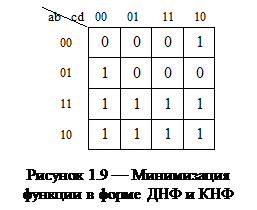
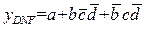(1.19),
а в результате склеивания минтермов, для которых функция у=0, получим выражение для исходной функции в минимальной КНФ:
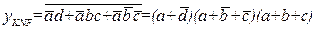(1.20).
Для записи логической функции y(a,b,c,d) в базисе И-НЕ применим к правым частям выражений (1.19), (1.20) правила двойного отрицания и правило де Моргана в разной последовательности. После преобразований получим:
(1.21),
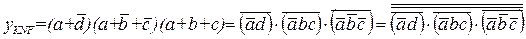(1.22).
Анализ выражений (1.21) и (1.22) показывает, что функциональная схема (рис. 1.10, а), реализующая заданную функцию в базисе И-НЕ, будет содержать меньшее количество элементов Шеффера (3<5), если её строить, используя выражение (1.21).
Для записи логической функции y(a,b,c,d) в базисе ИЛИ-НЕ применим к правой части выражений (1.19), (1.20) правило де Моргана и правило двойного отрицания в разной последовательности. После преобразований получим:
(1.23),
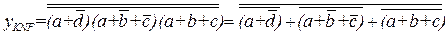(1.24).
Из анализа выражений (1.23) и (1.24) следует, что функциональные схемы, реализующие эти выражения, будут содержать одинаковое (4) количество элементов Пирса (для реализации 1.23 понадобится дополнительный элемент для заключительной инверсии). На рис. 1.10, б приведена функциональная схема, реализующая логическую функцию (1.24).
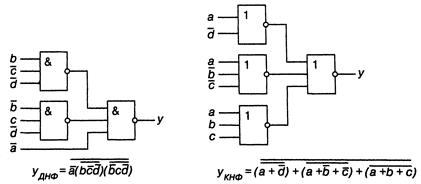
а б
Рисунок 1.10 — Аппаратная реализация логической функции: а — в базисе И-НЕ;
б — в базисе ИЛИ-НЕ
1.9 Коды и системы счисления
Существующие системы счисления подразделяются на позиционные и непозиционные. В непозиционных системах значение конкретной цифры постоянно и не зависит от ее расположения в записи числа. Примером такой системы счисления является Римская система записи числа. Например, в числе XXXVII значение цифры X не зависит от ее местоположения в записи числа. Оно везде равно 10.
В позиционных системах счисления значимость конкретной цифры определяется ее местоположением в записи числа. Так, произвольное число A в позиционной системе счисления с основанием q в общем случае можно представить в виде полинома:
,
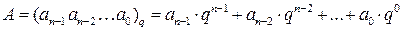где ai — разрядный коэффициент {ai=0,..., q–1}; q — весовой коэффициент или основание системы счисления.
Числа (кодовые слова) в цифровых устройствах обычно представляют в позиционной двоичной системе счисления.
Запись натурального числа А в позиционной двоичной системе счисления:
(1.25).
Представление дробных чисел, значения которых не превышают единицы:
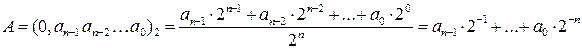(1.26).
В формулах (1.25, 1.26) а i — разрядные коэффициенты, принимающие значения 1 и 0; n —число разрядов в коде. Например, 26(10) =11010(2), n = 5.
Код, построенный по (1.25, 1.26), принято относить к арифметическим кодам, на которые распространяются арифметические операции сложения, вычитания, умножения и деления.
Число символов в кодовом слове цифрового устройства обычно фиксировано, т. е. кодовые слова имеют одинаковую длину. Если кодовое слово имеет n символов (разрядов), то из них можно составить N=2n комбинаций кодовых слов. Например, в 32-разрядном вычислительном устройстве можно закодировать 232 = 4 294 967 296 слов.
Для оценки количества цифровой информации используют бит и байт (1 байт=8 бит). 1 бит — это мера информации, выражающая такое её количество, которое может передать один символ двоичного алфавита при равной вероятности появления каждого символа алфавита:
I=log2m = log22 = 1 бит (1.27),
где m=2 — число символов в бинарном алфавите.
В цифровой электронике это понятие распространяют на двоичные системы с любым числом разрядов, полагая при этом информационную ёмкость каждого разряда, равной 1 биту. Так, в 8-разрядном слове информационная ёмкость равна 8 битам или 1 байту.
В цифровых вычислительных системах наряду с двоичной BIN широко используют также восьмеричную OCT (для кодирования адресов и команд), шестнадцатеричную HEX (цифробуквенную), двоичную-десятичную BCD системы счисления.
Ниже приведены символы алфавитов вышеперечисленных систем счисления.
BIN — 0, 1
OCT — 0, 1, 2, 3, 4, 5, 6, 7
HEX — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
BCD8-4-2-1 — 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001
Преобразование целой части числа из десятичной в другую форму счисления. Для преобразования целой части десятичного числа в иную систему счисления нужно последовательно делить ее на основание новой системы счисления и записывать остатки в качестве значащих цифр результата. Алгоритм такого преобразования имеет следующий вид:
1. Поделить десятичное число на основание новой системы счисления.
2. Сохранить остаток (первый остаток будет цифрой, стоящей в самом младшем значащем разряде).
3. Повторять шаги 1 и 2 до тех пор, пока частное не будет нулевым.
4. Записать остатки от деления на основание в обратном порядке (последний остаток будет старшим (крайним слева) разрядом преобразованного числа.
Пример. Преобразовать 25(10) в двоичную систему счисления.
Решение.
25:2= 12 + 1(ост)
12:2= 6 + 0(ост)
6:2 = 3 + 0(ост)
3:2 = 1 + 1(ост)
1:2 = 0 + 1(ост)
Итак, 25(2)=11001
Преобразование дробной части десятичного числа . Преобразование дробной части десятичного числа в другую систему счисления выполняет посредством умножения на значение основания системы счисления. Алгоритм для преобразования дробной части десятичного числа имеет следующий вид:
1. Умножить дробную часть на основание новой системы счисления.
2. Сохранить целую часть результата (даже если она нулевая) в качестве цифры. Обратите внимание на то, что первый результат записывается непосредственно справа от точки, разделяющей целую и дробную часть числа.
3. Повторять шаги 1 и 2, используя дробную часть шага 2 до тех пор, пока дробная часть не станет равной нулю. (Следует обратить внимание на то, что некоторые числа бесконечны — периодические дроби, следовательно, в этом случае процесс может продолжаться бесконечно).
4. Записать целые части от последовательных умножений в прямом порядке, начиная с первой справа позиции от точки, разделяющей целую и дробную части.
Пример. Преобразовать 0.12(10) в двоичную систему счисления.
0.12×2 = 0.24 + 0(целое)
0.24×2 = 0.48 + 0(целое)
0.48×2 = 0.96 + 0(целое)
0.96×2 = 0.92 + 1(целое)
0.92×2 = 0.84 + 1(целое)
0.84×2 = 0.68 + 1(целое)
0.68×2 = 0.36 + 1(целое)
0.36×2 = 0.72 + 0(целое)
0.72×2 = 0.44 + 1(целое)
…. ….
Итак, 0.12(2)»0.000111101
Действительное число 25.12(10)»11001.000111101(2)
Двоично-десятичные ( BCD) коды. BCD коды самодополняющиеся и несамодополняющиеся.
Особенность двоично-десятичных кодов состоит в том, что каждый разряд десятичного числа записывается в виде двоичного 4-хразрядного кода соответствующей десятичной цифры.
Таблица 1.5 — Некоторые двоичные и двоично-десятичные коды
| Десятичное число | Шестнадцатиричное число | Двоично-десятичные эквиваленты в различных кодах | Двоичный код 8-4-2-1 | Код Грея | |||||||
| Несамодополняющиеся | Самодополняющиеся двоично-десятичные | ||||||||||
| Код 8-4-2-1 | Код 2-4-2-1 | Код 4-2-2-1 | Код 5-2-1-1 | Код 5-4-2-1 | Код 2-4-2-1 | Код 4-2-2-1 | код с избыт-ком 3 | ||||
| 0 | 0 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0011 | 0000 | 0000 |
| 1 | 1 | 0001 | 0001 | 0001 | 0001 | 0001 | 0001 | 0001 | 0100 | 0001 | 0001 |
| 2 | 2 | 0010 | 0010 | 0010 | 0011 | 0010 | 0010 | 0010 | 0101 | 0010 | 0011 |
| 3 | 3 | 0011 | 0011 | 0011 | 0101 | 0011 | 0011 | 0101 | 0110 | 0011 | 0010 |
| 4 | 4 | 0100 | 0100 | 0110 | 0111 | 0100 | 0100 | 0110 | 0111 | 0100 | 0110 |
| 5 | 5 | 0101 | 0101 | 0111 | 1000 | 1000 | 1011 | 1001 | 1000 | 0101 | 0111 |
| 6 | 6 | 0110 | 0110 | 1010 | 1001 | 1001 | 1100 | 1010 | 1001 | 0110 | 0101 |
| 7 | 7 | 0111 | 0111 | 1011 | 1011 | 1010 | 1101 | 1101 | 1010 | 0111 | 0100 |
| 8 | 8 | 1000 | 1110 | 1110 | 1101 | 1011 | 1110 | 1110 | 1011 | 1000 | 1100 |
| 9 | 9 | 1001 | 1111 | 1111 | 1111 | 1100 | 1111 | 1111 | 1100 | 1001 | 1101 |
| 10 | A | 1010 | 1111 | ||||||||
| 11 | B | 1011 | 1110 | ||||||||
| 12 | С | 1100 | 1010 | ||||||||
| 13 | D | 1101 | 1011 | ||||||||
| 14 | E | 1110 | 1001 | ||||||||
| 15 | F | 1111 | 1000 | ||||||||
Каким образом можно представить десятичное число 926 в двоичной форме? Преобразование этого числа из десятичной системы в двоичную можно осуществить, пользуясь способом, описанным выше на стр. 20. Полученное двоичное число 1110011110 большинству из нас мало что говорит. Код, в котором двоичная система счисления используется несколько иным образом, чем в предыдущем примере, называется двоично-десятичным кодом 8421. Именно этот код часто имеют в виду, когда говорят просто о двоично-десятичном коде.
Преобразование десятичного числа 926 в этот код дает результат в виде последовательности двоичных тетрад 1001 0010 0110, каждая из которых кодирует соответствующую десятичную цифру.
Представьте, что вам дано число 0001 1000 0111 0001, записанное в BCD‑коде 8421. Какому десятичному числу оно соответствует? Чтобы узнать это, надо разбить число на тетрады слева направо и считать закодированные в двоичном коде десятичные цифры (187110).
В коде 8421 каждая десятичная цифра кодируется обычным позиционным 4-хразрядным двоичным числом. Этот код употребляется чаще других. Его преимущество перед другими заключается, во-первых, в том, что двоичные комбинации для одноразрядных десятичных чисел в нем такие же, как и при обычном двоичном счете, и, во-вторых, в том, что этот код однозначен: для каждого десятичного числа существует только одна соответствующая ему кодовая комбинация. Другие же коды неоднозначны. В табл. 1.5, например, показаны два кода 4-2-2-1, т. е. два кода с одинаковыми весами разрядов, но с разными двоичными комбинациями для одних и тех же десятичных чисел.
Наряду с кодом 8-4-2-1 находят широкое применение также и другие двоично-десятичные коды. При этом взвешенные коды (2-4-2-1, 5-4-2-1 и др.) применяются чаще, чем невзвешенные (код с изб. 3, 3а+2, 2 из 5), что объясняется тем, что взвешенные коды более приемлемы при построении цифро-аналоговых преобразователей.
Особую группу двоично-десятичных кодов образуют самодополняющиеся коды (код с изб. 3, 3а+2, 2-4-2-1, 4-2-2-1). Для самодополняющихся кодов характерно то, что при поразрядном инвертировании кодовой комбинации данного десятичного числа получается кодовая комбинация, дополняющая данное число до девяти (дополнение). Иначе говоря, в самодополняющемся коде обратные двоичные числа соответствуют обратным десятичным числам. Это свойство кода очень удобно при построении цифровых приборов, измеряющих как положительные, так и отрицательные величины, а также при реализации арифметических операций.
В коде с избытком 3 каждое десятичное число кодируется двоичным числом, на три единицы превышающем десятичное число, поэтому числу 0 соответствует код 0011, отображающий число 3; числу 9 соответствует код 1100, отображающий число 12;
Код 8421 очень широко применяется в цифровых системах. Как уже было отмечено, его часто называют просто двоично-десятичным кодом. Здесь, однако, следует соблюдать определенную осторожность, поскольку существуют двоично-десятичные коды и с другими весами числовых разрядов, например код 4221, код с избытком 3 и др.
Дата добавления: 2022-01-22; просмотров: 68; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!