Глава 2. Связь между непрерывностью и дифференцируемостью. Дифференциал функции.
Теорема. Если функция у(x) = f(x) дифференцируема в своей области определения, то она непрерывна. Обратное не верно: из непрерывности функции дифференцируемость не следует.
Доказательство. Дифференцируемость означает наличие производной
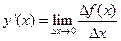(2.1)
Используем теорему о разности между функцией и ее пределом (раздел 3. Формула (3.1)):
если
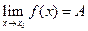, (2.2)
то
f (x) = A + a (х), (2.3)
где a (х) величина бесконечно малая.
Сравнивая выражения (2. 2) и (2. 3) получим, что в нашем случае
A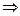 
y’(x), f(x)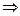 
, 
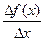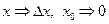
т.е.
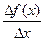= y’(x) +a (Δх). (2.4)
Умножим (2.4) на Δх
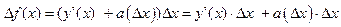. (2.5)
Из (2.5) следует, что если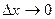 
, то и 
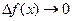, что является доказательством непрерывности функции (см. раздел 3).
Приведем пример показывающий, что непрерывная функция может быть не дифференцируемой. Возьмем функцию
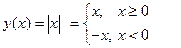
Эта функция непрерывна на всей области определения, так как в точке х0 = 0 выполняется соотношение (см. раздел 3)
|
|
|
= 
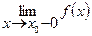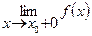= f(x0).
Действительно
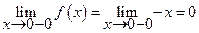
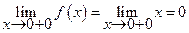= f(x0).
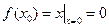
Следовательно в точке 0 функция непрерывна.
Но производной в этой точке нет, так как слева при x < 0, y’(x) = -1, а справа при x > 0 y’(x) = 1.
Вернемся к формуле (2.5). Дифференциалом df(x) функции f(x) в точке х называется линейная по Dx часть приращения функции
df(x) =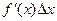 
. (2.6)
По определению для независимой переменной Δх = dx. Поэтому дифференциал функции f(x) записывают чаще так
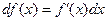(2.7)
Формула (2.7) сохраняется и в том случае, когда х зависимая переменная (формула (2.6) для зависимой переменной неверна).
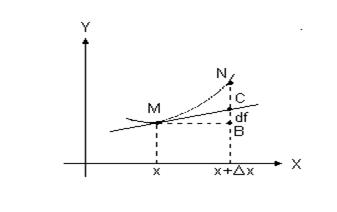
Геометрический смысл дифференциала (рис.2.1).
Производная f ¢(x) численно равна тангенсу угла наклона касательной к графику функции f(x). Дифференциал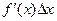 
равен изменению ординаты, касательной к функции в точке N. Замена истинного приращения функции NB Df(x) = f(x + Dx) - f(x) на дифференциал СВ 
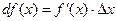равносильна замене части графика функции на соответствующую часть касательной к этому графику (см. также рис.1.1).
|
|
|
Производная f¢(x) является функцией того же аргумента х, что и исходная функция. Поэтому ее можно опять дифференцировать, т.е. вычислять предел отношения приращения производной к приращению аргумента
= 
.
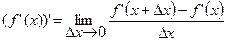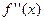Если этот предел существует и конечен, то он называется второй производной от функции f(x) в точке х. Принятое обозначение:
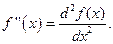
Подобным образом вводят производные n-го порядка f(n)(x) = (f(n-1)(x))¢.
В механике вторая производная от пути по времени есть ускорение
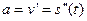
Пример 1. Производные от степенной функции y = хn.
y¢ = n xn-1,
y¢¢ = n (n-1) xn-2,
y¢¢¢ = n (n-1) (n-2) xn-3,
...,
y(k) = n (n-1) (n-2)...(n-k+1) x(n-k) при (к £ n).
Пример 2. Точка совершает прямолинейное колебательное движение по закону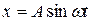 
. Найти скорость и ускорение точки в момент времени 
.
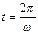Решение. Найдем скорость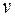 
и ускорение а в любой момент времени t
; 
.
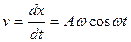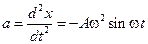При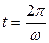 
, 
.
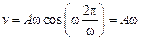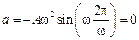Дифференциалом второго порядка называется дифференциал от первого дифференциала
d(df(x)) = (df(x))¢Dx = (f ¢(x)Dx)¢Dx = f ¢¢(x) (Dx)2
Пример. Вычислить производную функции заданной параметрически
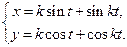
Функция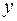 
от независимой переменной 
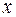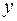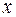задана через посредство вспомогательной переменной (параметра t). Производная от по определяется формулой
|
|
|
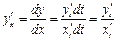
Находим производные от 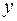и 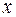по параметру t:
, 
,
.
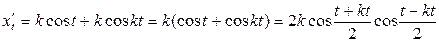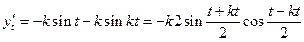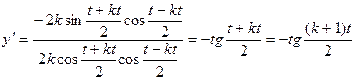Дата добавления: 2022-01-22; просмотров: 48; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!