ЗАГАЛЬНА ЗАДАЧА ЛІНІЙНОГО ПРОГРАМУВАННЯ ТА МЕТОДИ ЇЇ РОЗВ'ЯЗУВАННЯ
Математична постановка задач лінійного програмування. Система гіпотез.
Загальна лінійна математична модель економічних процесів і явищ — так звана загальна задача лінійного програмування (ЛП) подається у вигляді:
знайти максимум (мінімум) функції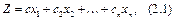 
або 
за умов
Отже, потрібно знайти значення змінних 
, які задовольняють умови (2.2) і (2.3), тоді як цільова функція набуває екстремального (максимального чи мінімального) значення.
Задачу (2.1)—(2.3) легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (2.2) всі 
невід'ємні, а всі обмеження є рівностями.
Якщо якесь bi від'ємне, то, помноживши i-те обмеження на (–1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності 
то останню завжди можна звести до рівності, увівши допоміжну змінну 
.
Аналогічно обмеження виду 
зводимо до рівності, віднімаючи від лівої частини допоміжну змінну 
, тобто 
.
Приклад 2.1. Записати в канонічній формі таку задачу ЛП:
за умов
Розв'язування. Помножимо другу нерівність на (–1) і введемо відповідно допоміжні змінні x 4 і x 5 для другого та третього обмеження:
Неважко переконатися, що допоміжні змінні, у цьому разі x4 і x5, є невід'ємними, причому їх уведення не змінює цільової функції.
Отже, будь-яку задачу ЛП можна записати в такій канонічній формі:
знайти максимум функції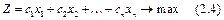 
за умов
Задачу (2.4)—(2.6) можна розв'язувати на мінімум, якщо цільову функцію помножити на (–1), тобто
|
|
|
2.2. Визначення множини допустимих планів задачі ЛП
Задачу ЛП (ЗЛП) зручно записувати за допомогою знака суми «S». Справді, задачу (2.4)—(2.6) можна подати так:
за умов
Ще компактнішим є запис ЗЛП у векторно-матричному вигляді:
за умов
де
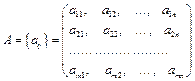
є матриця коефіцієнтів при змінних
– вектор змінних; 
– вектор вільних членів;
— вектор коефіцієнтів при змінних у цільовій функції.
Часто ЗЛП зручно записувати у векторній формі:
за умов
де
є вектори коефіцієнтів при змінних.
2.3. Геометрична інтерпретація ЗЛП . Кононічна форма ЗЛП і її оптимальний план.
Геометричну інтерпретацію ЗЛП розглянемо на такому прикладі. Нехай фермер прийняв рішення вирощувати озиму пшеницю і цукровий буряк на площі 20 га, відвівши під цукровий буряк не менш як 5 га. Техніко-економічні показники вирощування цих культур наведені в таблиці:
| № з/п | Техніко-економічний показник із розрахунку на 1 га | Сільськогосподарська культура | Наявний ресурс | |
| Озима пшениця | Цукровий буряк | |||
| 1 | Жива праця, людино-днів | 5 | 25 | 270 |
| 2 | Механізована праця, людино-днів | 2 | 8 | 80 |
| 3 | Прибуток, тис. грн. | 0,7 | 1 | |
|
|
|
Критерієм оптимальності є максимізація прибутку.
Запишемо економіко-математичну модель структури виробництва озимої пшениці та цукрового буряка, скориставшись такими позначеннями:
x 1 — шукана площа посіву озимої пшениці;
x2 — шукана площа посіву цукрового буряка.
ЗЛП має вигляд:
за умов
Геометричну інтерпретацію задачі наведено на рис. 2.1.
Область допустимих розв'язків дістаємо так. Кожне обмеження, наприклад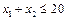 
, задає півплощину з граничною прямою 
. Будуємо її і визначаємо півплощину, яка описується нерівністю 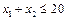. З цією метою в нерівність 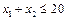підставляємо координати якоїсь характерної точки, скажімо 
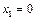і 
. Переконуємося, що ця точка належить півплощині 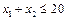. Цей факт на рис. 2.1 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (2.8)—(2.12). У результаті перетину цих півплощин утворюється область допустимих розв'язків задачі (на рис. 2.1 — многокутник ABCD ). Цільова функція 
описує сім'ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z = 0, маємо 
. Ця пряма проходить через початок системи координат. Коли Z = 3,5, дістаємо пряму 
.
Загальна задача лінійного програмування (2.1)—(2.3) геометричне інтерпретується так: кожне і-те обмеження, що має вигляд рівняння
|
|
|
у n-вимірному просторі основних змінних задає гіперплощину. Кожному обмеженню виду (2.2) і (2.3) відповідають гіперплощина та півпростір, який лежить по один бік цієї гіперплощини. У перетині всіх півпросторів, що визначаються обмеженнями задачі (2.2) і (2.3), утворюється опуклий многогранник допустимих її розв'язків. Цільову функцію
в n-вимірному просторі основних змінних можна геометричне інтерпретувати як сім'ю паралельних гіперплощин, положення кожної з яких визначається значенням параметра Z.
2.4. Основні аналітичні властивості розв'язків задач лінійного програмування
Вектор 
, координати якого задовольняють системі обмежень (2.2) і (2.3), називають допустимим розв'язком, або допустимим планом задачі. Сукупність допустимих розв'язків (планів) задачі утворює область допустимих розв'язків задачі.
Опорним планом задачі лінійного програмування називається план, утворений координатами вершини многогранника планів задачі. Отже, опорний план — це план, який задовольняє не менш ніж п лінійно незалежних обмежень (2.2) у вигляді строгих рівностей разом з обмеженням (2.3) щодо знака.
|
|
|
Опорний план називається невиродженим, якщо він є вершиною многогранника планів задачі, утвореного перетином точно п гіперплощин, тобто задовольняє п лінійно незалежних обмежень — строгих рівностей. У противному разі опорний план є виродженим.
Якщо задача лінійного програмування має розв'язок і серед її планів є опорні, то хоча б один із них буде оптимальним.
Сукупність усіх розв'язків задачі лінійного програмування є многогранною опуклою множиною, яку називають многогранником розв'язків.
Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин многогранника розв'язків. Якщо цільова функція набуває екстремального значення більш як в одній вершині цього многогранника, то вона досягає його і в будь-який точці, що є лінійною комбінацією таких вершин.
2.5. Графічний метод розв'язування задач лінійного програмування
2.5.1. Основи графічного методу
Для розв'язування двовимірних задач лінійного програмування, тобто задач з двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Розглянемо таку задачу. Знайти екстремум (мінімум, максимум) функції:
за умов
Припустимо, що система (2.14) за умов (2.15) сумісна і многокутник її розв'язків обмежений.
Згідно з геометричною інтерпретацією задачі лінійного програмування (2.4) кожне i-те обмеження-нерівність (2.14) визначає півплощину з граничною прямою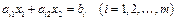 
. Системою обмежень (2.14) описується спільна частина, або переріз усіх зазначених півплощин, тобто множина точок, координати яких задовольняють всі обмеження задачі. Таку множину точок називають многокутником розв'язків, або областю допустимих планів (розв'язків) задачі лінійного програмування.
Умова (2.15) невід'ємності змінних означає, що область допустимих розв'язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометричне інтерпретується як сім'я паралельних прямих 
Сформулюємо деякі властивості задачі лінійного програмування, застосовувані під час її графічного розв'язування.
Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин многокутника розв'язків. А якщо цільова функція досягає екстремального значення більш як в одній вершині многокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.
Отже, розв'язати задачу лінійного програмування графічно означає знайти таку вершину многокутника розв'язків, у результаті підставляння координат якої в (2.13) лінійна цільова функція набуває найбільшого (найменшого) значення.
Алгоритм графічного методу розв'язування задач лінійного програмування складається з розглянутих далі кроків.
1. Будуємо прямі лінії, рівняння яких дістаємо заміною в обмеженнях задачі (2.14) знаків нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3. Знаходимо многокутник розв'язків задачі лінійного програмування.
4. Будуємо вектор 
, що задає напрям зростання значень цільової функції задачі.
5. Будуємо пряму 
, перпендикулярну до вектора 
.
6. Переміщуючи пряму в напрямі вектора (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину многокутника розв'язків, де цільова функція досягає екстремального значення.
7. Визначаємо координати точки, в якій цільова функція набуває максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
У разі застосування графічного методу для розв'язування задач лінійного програмування можливі такі випадки.
Цільова функція набуває максимального значення в єдиній вершині А многокутника розв'язків (рис. 2.2).
Максимального значення цільова функція досягає в будь-якій точці відрізка АВ (рис. 2.3). Тоді задача лінійного програмування має альтернативні оптимальні плани.
Задача лінійного програмування не має оптимальних планів (рис. 2.4 — цільова функція не обмежена згори; рис. 2.5 — система обмежень задачі несумісна).
Задача лінійного програмування має оптимальний план за необмеженої області допустимих розв'язків (рис. 2.6 і 2.7). На рис. 2.6 у точці В маємо максимум, на рис. 2.7 у точці В — мінімум, на рис. 2.8 показано, що в разі необмеженої області допустимих планів цільова функція набуває максимальне і мінімальне значення.
2.5.2. Навчальні завдання. Розв'язування задач графічним методом
Розглянемо застосування графічного методу для розв'язування деяких економічних задач.
Задача 2.1. Фірма спеціалізується на виробництві офісних меблів, зокрема вона випускає дві моделі збірних книжкових полиць — А та В. Полиці обох моделей обробляють на верстатах 1 та 2. Тривалість обробки (у хвилинах) однієї полиці кожної моделі подано таблицею.
| Верстати | Тривалість обробки полиці, хв., за моделями | |
| А | В | |
| 1 | 30 | 15 |
| 2 | 12 | 26 |
Час роботи верстатів 1 та 2 становить відповідно 40 та 36 год. на тиждень. Прибуток фірми від реалізації однієї полиці моделі А дорівнює 50 у. о., а моделі В — 30 у. о. Вивчення ринку збуту показало, що тижневий попит на книжкові полиці моделі А ніколи не перевищує попиту на модель В більш як на 30 одиниць, а попит на полиці моделі В не перевищує 80 одиниць на тиждень.
Визначити обсяги виробництва книжкових полиць різних моделей, що максимізують прибуток фірми. Побудувати економіко-математичну модель поставленої задачі та розв'язати її графічно.
Побудова математичної моделі. Змінними в моделі є тижневі обсяги виробництва книжкових полиць моделей А та В. Нехай х1 — кількість полиць моделі А, виготовлюваних фірмою за тиждень, а x 2 — відповідна кількість полиць моделі В. Цільова функція моделі — максимізація прибутку фірми від реалізації продукції. Математично вона записується так:
Обмеження математичної моделі враховують час роботи верстатів 1 та 2 для обробки продукції та попит на полиці різних моделей. Обмеження на час роботи верстатів 1 та 2 набирають такого вигляду:
для верстата 1 - 
хв.;
для верстата 2 - 
хв.
Обмеження на попит набирають вигляду:
Отже, економіко-математичну модель поставленої задачі можна записати так:
Записана економіка-математична модель є моделлю задачі лінійного програмування, що містить лише дві змінні, і тому може бути розв'язана графічно.
Розв'язування. Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто в побудові такої області, де одночасно виконуються всі обмеження моделі. Замінюємо знаки нерівностей на знаки строгих рівностей і будуємо графіки відповідних прямих (рис. 2.9). Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї задовольняють розглядувану нерівність, а іншої — не задовольняють. Щоб визначити необхідну півплощину (на рис. 2.9 її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. У протилежному разі таким зображенням є інша півплощина. Умова невід'ємності змінних 
обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі, — шестикутник OABCDE . Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід'ємності змінних. Тому поставлену задачу буде розв'язано, якщо ми зможемо відшукати таку точку многокутника OABCDE , в якій цільова функція Z набуває найбільшого значення.
Для цього побудуємо вектор , компонентами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор завжди виходить із початку координат і напрямлений до точки з координатами 
. У нашій задачі вектор 
. Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.
Побудуємо лінію, що відповідає, наприклад, значенню Z = 0. Це буде пряма 
, яка перпендикулярна до вектора і проходить через початок координат. Оскільки маємо визначити найбільше значення цільової функції, пересуватимемо пряму в напрямі вектора доти, доки не визначимо вершину многокутника, яка відповідає оптимальному плану задачі.
Із рис. 2.9 бачимо, що останньою спільною точкою прямої цільової функції та многокутника OABCDE , є точка С. Координати цієї точки визначають оптимальний план задачі, тобто обсяги виробництва книжкових полиць моделей А та В, що максимізують прибуток від їх реалізації.
Координати точки С визначаються перетином прямих (2.17) і (2.18):
Розв'язавши цю систему рівнянь, дістанемо 
. Отже, 
Це означає, що коли фірма щотижня виготовлятиме 50 збірних книжкових полиць моделі А та 60 — моделі В, то вона отримає максимальний прибуток 4300 у. о. При цьому тижневий фонд роботи верстатів 1 та 2 буде використано повністю.
Задача 2.2 Невелика птахоферма має розрахувати оптимальний кормовий раціон для 1000 курчат, яких вирощують до 8-тижневого віку. Нехтуючи тим, що тижневі витрати кормів для курчат залежать від їхнього віку, вважатимемо, що в середньому за 8 тижнів вони досягнуть маси 500 г. З цією метою кормовий раціон курчат має задовольняти певні вимоги поживності. Сформулюємо ці вимоги у спрощеному вигляді, ураховуючи лише дві поживні речовини: білок і клітковину, що містяться у кормах двох видів — зерні та соєвих бобах. Вміст поживних речовин у кожному кормі та їх вартість задано таблицею:
| Корм | Вміст поживних речовин, % | Вартість 1 кг корму, у.о. | |
| Білок | Клітковина | ||
| Зерно | 10 | 2 | 0,40 |
| Соєві боби | 50 | 8 | 0,90 |
Готова кормова суміш має містити не менш як 20 % білка і не більш як 5 % клітковини.
Визначити масу кожного з двох видів кормів, що утворюють кормову суміш мінімальної вартості, задовольняючи вимоги до загальних витрат кормової суміші та її поживності.
Побудова математичної моделі. Нехай x 1 — маса, кг, зерна в кормовій суміші, а x 2 — вміст, кг, соєвих бобів у готовій кормовій суміші.
Загальна кількість суміші 
має становити не менш як 1000 • 0,5 = 500 (кг), тобто
Розглянемо обмеження щодо поживності кормової суміші.
1. Суміш має містити не менш як 20 % білка:
2. Суміш має містити не більш як 5 % клітковини:
Остаточно математична модель задачі оптимізації кормового раціону набирає такого вигляду:
Розв'язування. Графічну інтерпретацію задачі подано на рис. 2.10. Множина допустимих її розв'язків необмежена. Для вектора 
можна змінити масштаб, наприклад 
Найменшого значення цільова функція Z досягає в точці А, що лежить на перетині прямих (2.23) та (2.24). Визначимо її координати:
Отже, 
.
 |
Знайдений оптимальний план задачі показує: для того щоб отримати 500 кг кормової суміші мінімальної вартості (262,50 у. о.), потрібно взяти 375 кг зерна та 125 кг соєвих бобів. При цьому вимоги до поживності кормової суміші виконуватимуться:
0,10 • 375 + 0,50 • 125= 100кг білка, що становить рівно 20 % загальної маси суміші;
0,02 • 375 + 0,08 • 125 = 17,5 кг клітковини в кормовій суміші, що становить 3,5 % її маси і не перевищує 5 %.
Задача 2.3. Фірма виготовляє два продукти А та В, що продаються відповідно по 8 та 15 центів за упаковку. Ринок збуту для кожного з них практично необмежений. Продукт А обробляється верстатом 1, а продукт В — верстатом 2. Далі обидва продукти упаковуються на фабриці. Схему виробництва продуктів А та В показано на рис. 2.11.
Ціна 1 кг сировини — 6 центів. Верстат 1 обробляє за годину 5000 кг сировини, а верстат 2 — 4000 кг сировини із втратами, що становлять відповідно 10 і 20%. Верстат 1 може працювати 6 год. на день, причому його використання коштує 288 дол./год.; верстат 2 – 5 год на день, що коштує 336 дол./год.
Маса однієї упаковки продукту А дорівнює 1/4 кг, а продукту В 1/3 кг. Фабрика може працювати 10 год на день, виготовляючи за 1 год. продукції на 360 дол. упаковуючи 12 000 продуктів А та 8000 продуктів В.
Відшукати такі значення х1 та х2 споживання сировини для продуктів А та В (у тисячах кілограмів), які забезпечують найбільший щоденний прибуток фірми.
Сформулюємо математично задачу й розв'яжемо її графічно.
Побудова математичної моделі. Нехай х1 —кількість сировини, тис. кг, використовуваної для виготовлення продукту А, а х2 —— кількість сировини, тис. кг, що йде на виготовлення продукту В.
Запишемо обмеження задачі. Згідно з умовою обмеженими ресурсами є час використання верстатів 1 і 2, а також час роботи фабрики з упакування продуктів А та В
1. Обмеження на використання верстата 1. Економічний зміст цього обмеження такий: фактичний час роботи верстата 1 з обробки сировини для продукту А не повинен перевищувати 6 год, тобто
| Кількість сировини для продукту А, тис. кг | £ 6 год. |
| Продуктивність верстата, тис. кг/год |
Математично це запишеться так:
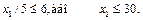
2. Обмеження на використання верстата 2 знаходимо аналогічно:
3. Обмеження на час роботи фабрики з упакування продуктів А та В.
Економічний зміст цього обмеження такий: фактичний час, витрачений на упакування продуктів А та В, не повинен перевищувати 10 год на день:
| Кількість сировини для продукту А – - Витрати сировини під час обробки, тис. кг | + |
| Маса упаковки продукту А, тис. кг × ×Продуктивність під час упакування продукту А, шт./год |
| + | Кількість сировини для продукту В, - - Витрати сировини під час обробки, тис. кг | £ 10 год |
| Маса упаковки продукту В, тис. кг × × Продуктивність під час упакування продукту В, шт./год |
Математично це запишеться так:
або
Побудуємо цільову функцію задачі. Прибуток фірми складається з різниці між доходом від реалізації виготовленої продукції та витратами на її виробництво.
1. Дохід, дол., від виробництва продуктів А та В визначається так:
| Кількість сировини, що надходить на упакування, тис. кг | × | Ціна упаковки, дол., |
| Маса упаковки продукту, тис. кг |
або
Загальний дохід дорівнює 
.
2. Витрати, дол., на сировину визначаємо як загальну кількість сировини, тис. кг, використовуваної для виробництва продуктів А та В, помножену на вартість одиниці сировини, дол.:
3. Витрати, дол., пов'язані з використанням верстатів 1 і 2, визначаємо як фактичний час роботи верстата з обробки сировини, помножений на вартість 1 год роботи відповідного верстата:
4. Витрати, дол., пов'язані з упакуванням продуктів А та В, складаються з фактичного часу роботи фабрики 
, помноженого на вартісний еквівалент 1 год роботи фабрики, який становить 360 дол.:
Узагальнюючи всі складові частини цільової функції, можемо записати математичний вираз прибутку фірми за день:
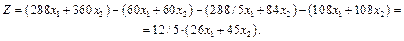
Отже, маємо остаточний запис економіко-математичної моделі:
за обмежень
Незважаючи на порівняно складний процес моделювання, математично поставлена задача дуже проста й легко розв'язується графічно.
Розв'язування. Графічне розв'язування задачі ілюструє рис. 2.12. Областю допустимих планів, що утворюється системою обмежень задачі, є многокутник OABCD . Найбільшого значення цільова функція досягає у вершині В. Координати цієї точки визначаються із системи рівнянь:
Оптимальний план задачі 
.
Отже, для того, щоб отримати найбільший денний прибуток 2992 дол., фірма має обробляти 40/3 тис. кг сировини, виробляючи продукт А, і 20 тис. кг — виробляючи продукт В. За такого оптимального плану випуску продукції верстат 2 працюватиме 20/4=5 год на день, тобто з повним навантаженням, а верстат 1 працюватиме лише 40/15 = 2 год 20 хв на день.
Задача 2.4. На меблевій фабриці зі стандартних листів фанери потрібно вирізати 24, 28 і 18 заготовок трьох розмірів. Лист фанери можна розрізати двома способами. Кількість отриманих заготовок та площу відходів за кожного способу розрізування одного листа фанери наведено в таблиці:
| Заготовка | Кількість отриманих заготовок, шт., за способами | |
| першим | другим | |
| 1 2 3 | 2 4 2 | 6 4 3 |
| Площа відходів, см2 | 12 | 18 |
Скільки листів фанери та за яким способом слід розрізати, щоб отримати потрібну кількість заготовок з мінімальними відходами.
Побудова математичної моделі. Нехай 
— кількість листів фанери, які необхідно розрізати відповідно першим і другим способом.
Цільова функція — мінімізація відходів під час розрізування листа фанери. Математично це записується так:
Обмеження математичної моделі враховують кількість заготовок кожного виду, які потрібно отримати:
| для заготовки 1 для заготовки 2 для заготовки 3 | 
|
Отже, економіко-математична модель задачі має вигляд
за обмежень
Розв'язування. Графічне розв'язування задачі оптимального розрізування ілюструє рис. 2.13. Область допустимих розв'язків цієї задачі необмежена. Вектор = (12; 18) можна змінити згідно з масштабом графіка, наприклад = (6; 9).
Із рис. 2.13 бачимо, що пряма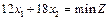 
збігається зі стороною ВС многокутника розв'язків. Це означає, що задача має альтернативні оптимальні плани: координати будь-якої точки відрізка ВС є оптимальним планом, причому для цих координат цільова функція Z досягає свого найменшого значення. Визначимо лише два оптимальних плани, що відповідають кінцям відрізка ВС.
Точка В утворюється перетином прямих (2.29) і (2.30); її координати визначаємо із системи рівнянь
звідки 
.
Точка С лежить на перетині прямих (2.28) і (2.30); її координати визначаємо із системи рівнянь
отже, 
.
Повертаючись до економічного змісту розв'язаної задачі, маємо такі результати. Якщо розрізати 7 листів фанери, з яких 3 листи — першим способом, а 4 — другим, то матимемо найменшу площу відходів — 108 см. Але такі самі мінімальні втрати будуть і в разі розрізування шести листів першим способом і двох — другим.
Будь-який інший альтернативний оптимальний план задачі можна записати як опуклу лінійну комбінацію отриманих двох крайніх розв'язків:
де 
.
Наприклад, нехай 
Тоді ще один оптимальний план задачі визначається так:
Цільова функція Z має таке саме мінімальне значення: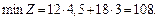 
2.6. Симплексний метод розв'язування задач ЛП. Інші методи.
2.6.1. Теоретичні відомості
Графічний метод для визначення оптимального плану задачі лінійного програмування доцільно застосовувати лише для задач із двома змінними. За більшої кількості змінних вдаються до загального методу розв'язування задач лінійного програмування — так званого симплекс-методу. Процес розв'язування задачі симплекс-методом має ітераційний характер: обчислювальні процедури (ітерації) одного й того самого типу повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або з'ясовано, що його не існує.
Отже, симплекс-метод — це поетапна обчислювальна процедура, в основу якої покладено принцип послідовного поліпшення значень цільової функції переходом від одного опорного плану задачі лінійного програмування до іншого.
Алгоритм розв'язування задачі лінійного програмування симплекс-методом складається з п'яти етапів:
1. Визначення початкового опорного плану задачі лінійного програмування.
2. Побудова симплексної таблиці.
3. Перевірка опорного плану на оптимальність за допомогою оцінок 
. Якщо всі оцінки задовольняють умову оптимальності, то визначений опорний план є оптимальним планом задачі. Якщо хоча б одна з оцінок не задовольняє умову оптимальності, то переходять до нового опорного плану або встановлюють, що оптимального плану задачі не існує.
4. Перехід до нового опорного плану задачі виконується визначенням розв'язувального елемента та розрахунком нової симплексної таблиці.
5. Повторення дій починаючи з п. 3. Розглянемо докладніше кожний з етапів алгоритму.
1. Визначення першого опорного плану починають із запису задачі лінійного програмування в канонічній формі, тобто у вигляді обмежень-рівнянь з невід'ємними правими частинами. Якщо в умові задачі присутні обмеження-нерівності, то перетворення їх на рівняння виконується за допомогою додаткових змінних, які вводяться до лівої частини обмежень типу « £ » зі знаком « + », а до обмежень типу « ³ » — зі знаком « - ». У цільовій функції задачі додаткові змінні мають коефіцієнт нуль.
Після зведення задачі до канонічного вигляду її записують у векторній формі. За означенням опорного плану задачі лінійного програмування його утворюють т одиничних лінійно незалежних векторів, які становлять базис m - вимірного простору (де т — кількість обмежень у задачі лінійного програмування).
На цьому етапі розв'язування задачі можливі такі випадки:
• після запису задачі у векторній формі в системі обмежень є необхідна кількість одиничних векторів. Тоді початковий опорний план визначається безпосередньо без додаткових дій;
• у системі обмежень немає необхідної кількості одиничних незалежних векторів. Тоді для побудови першого опорного плану застосовують метод штучного базису. Ідея його полягає в тому, що відсутні одиничні вектори можна дістати, увівши до відповідних обмежень деякі змінні з коефіцієнтом +1, які називаються штучними. У цільовій функції задачі лінійного програмування штучні змінні мають коефіцієнт +М (для задачі на min) або -М (для задачі на max), де М—досить велике додатне число.
Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні – вільними. Їх прирівнюють до нуля та з кожного обмеження задачі визначають значення базисних змінних. У такий спосіб отримують початковий опорний план задачі лінійного програмування.
2. Подальший обчислювальний процес та перевірку опорного плану на оптимальність подають у вигляді симплексної таблиці.
У першому стовпчику таблиці – «Базис» – записують базисні змінні опорного плану, причому в тій послідовності, в якій вони розміщуються в системі обмежень задачі.
Наступний стовпчик симплексної таблиці – «Сбаз» – коефіцієнти при базисних змінних у цільовій функції задачі.
У третьому стовпчику – «План» – записують значення базисних змінних і відшукуванні у процесі розв'язування задачі компоненти оптимального плану.
У решті стовпчиків симплексної таблиці, кількість яких відповідає кількості змінних задачі, записують відповідні коефіцієнти з кожного обмеження задачі лінійного програмування.
3. Перевіряють опорний план на оптимальність згідно з наведеною далі теоремою.
! Теорема (ознака оптимальності опорного плану). Опорний план 
задачі лінійного програмування є оптимальним, якщо для всіх 
виконується умова
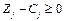(для задачі на max)
або
(для задачі на min)
Якщо для побудови опорного плану було використано метод штучного базису, необхідною умовою оптимальності є також вимога, щоб у процесі розв'язування задачі всі штучні змінні були виведені з базису і дорівнювали нулю.
Значення оцінок визначають за формулою
або безпосередньо із симплексної таблиці як скалярний добуток векторів-стовпчиків «Сбаз» та «xj» мінус відповідний коефіцієнт С j. Розраховані оцінки записують в окремий рядок симплексної таблиці, який називають оцінковим.
У процесі перевірки умови оптимальності можливі такі випадки:
а) усі 
задовольняють умову оптимальності, і тоді визначений опорний план є оптимальним;
б) не всі 
задовольняють умову оптимальності, і тоді потрібно виконати перехід до наступного, нового опорного плану задачі.
4. Перехід від одного опорного плану до іншого виконується зміною базису, тобто виключенням з нього деякої змінної та введенням замість неї нової з числа вільних змінних задачі.
Змінна, яка включається до нового базису, відповідає тій оцінці , що не задовольняє умову оптимальності. Якщо таких оцінок кілька, серед них вибирають найбільшу за абсолютною величиною і відповідну їй змінну вводять до базису. Припустимо, що індекс зазначеної змінної j = k. Відповідний стовпчик симплексної таблиці називають напрямним.
Для визначення змінної, що має бути виключена з базису, знаходять для всіх додатних аik напрямного стовпчика величину 
. Вибирають найменше значення 
, яке вказує на змінну, що виводиться з базису. Припустимо, що це виконується для і = r. Відповідний рядок симплексної таблиці називатиметься напрямним.
Перетином напрямного стовпчика та напрямного рядка визначається число симплексної таблиці а rk, яке називають розв'язувальним елементом. За допомогою елемента а rk , і методу Жордана-Гаусса розраховують нову симплексну таблицю.
Далі ітераційний процес повторюють доти, доки не буде визначено оптимальний план задачі.
У разі застосування симплекс-методу для розв'язування задач лінійного програмування можливі такі випадки.
1. Якщо в оцінковому рядку останньої симплексної таблиці оцінка 
відповідає вільній (небазисній) змінній, то це означає, що задача лінійного програмування має альтернативний оптимальний план. Отримати його можна, вибравши розв'язувальний елемент у зазначеному стовпчику таблиці та здійснивши один крок симплекс-методом.
2. Якщо при переході у симплекс-методі від одного опорного плану задачі до іншого в напрямному стовпчику немає додатних елементів а rk , тобто неможливо вибрати змінну, яка має бути виведена з базису, то це означає, що цільова функція задачі лінійного програмування є необмеженою й оптимальних планів не існує.
3. Якщо для опорного плану задачі лінійного програмування
всі оцінки 
задовольняють умову оптимальності, але при цьому хоча б одна штучна змінна є базисною і має додатне значення, то це означає, що система обмежень задачі несумісна й оптимальних планів такої задачі не існує.
ТЕМА 3
Дата добавления: 2022-01-22; просмотров: 21; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!