Линейные комбинации двух и более радикалов.
Если уравнение содержит два и более радикала, то необходимо придерживаться следующих правил:
1. указать область допустимых значений уравнения
2. распределить радикалы по обеим частям, чтобы обе части уравнения стали неотрицательными
3. только после этого возводить в квадрат левую и правую части уравнения.
Пример: Решить иррациональное уравнение:

Решение:
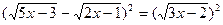

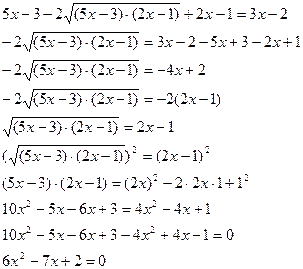
а=6, b=-7, с=2
х1,2=  =
= 

х1=  х2=
х2= 
Проверка:
1) х1= 
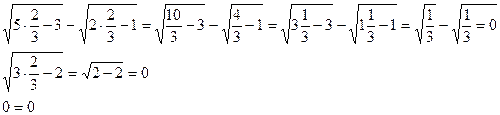
2) х2=  - не уд
- не уд
 ( по определению
( по определению  , а≥0 )
, а≥0 )
Ответ:х= 
Задание 14:Закончить решение уравнения:  .
.
Решение:

………………………………….
Ответ:…………….
Задание 15: Решить иррациональное уравнение:
1) 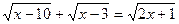
2) 
Проверь себя!
| Решить иррациональное уравнение: |
1. 
|
2. 
|
3. 
|
4. 
|
5. 
|
Тема 3. Решение иррациональных неравенств
Определение: Если в неравенство входят функции под знаком корня, то такие неравенства называют иррациональными
Неравенства вида 
данное неравенство равносильно системе неравенств: 
Пример :Решить неравенство 
Решение:
Сразу перейдём к равносильной системе:


Ответ. 
Задание 1: Закончить решение неравенства 
Решение :
Перейдём к равносильной системе:

………………………………
Ответ. 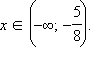
Задание 2: Решить иррациональные неравенства:
1) 
2) 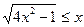
Неравенства вида 
данное неравенство равносильно совокупности неравенств:

|
|
|
Задание 3: Решить иррациональные неравенства:
1) 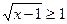
2) 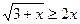
Неравенства вида 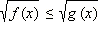
данное неравенство равносильно системе неравенств:

Пример :Решить неравенство 
Решение:
Перейдём к равносильной системе:

Решая эту систему методом интервалов, сразу получаем:
Ответ. 
Неравенство вида 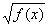 >
> 
данное неравенство равносильно системе неравенств:
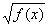 >
>  →
→ 
Задание 4: Решить иррациональные неравенства:
1) 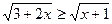
2) 
Проверь себя!
| Решить иррациональное неравенство: |
1.  >3 >3
|
2.  >4 >4
|
3.  <1 <1
|
4.  >4 >4
|
5. 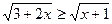
|
6. 
|
Тема 4. Решение систем двух уравнений с двумя неизвестными
Историческая справка
Ещё со времен вавилонян и древних индусов считается, что одной из основных целей алгебры является решение уравнений и их систем.
В древнем Вавилоне более 4000 лет назад умели решать уравнения первой, второй и некоторые уравнения третьей степени. Однако, общей теории уравнений в те времена ещё не было.
Приведём задачу, найденную в папирусе Кахуна (XVIII- XVI вв. до н.э.). Задача сформулирована в современных обозначениях и сводится по существу к решению системы уравнений: «Найдите числа ч и у, для которых х2 +у2 =100 и  ». В папирусе решена задача методом «ложного положения». «Положим х=1, тогда у=
». В папирусе решена задача методом «ложного положения». «Положим х=1, тогда у=  и х2 +у2=
и х2 +у2=  . Но в условии х2 +у2=102, значит, в качестве х нужно брать не 1, а 10:
. Но в условии х2 +у2=102, значит, в качестве х нужно брать не 1, а 10: 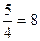 . Тогда у=6».
. Тогда у=6».
|
|
|
В древности уравнениям придавалась геометрическая форма. Сегодня напоминания о «геометрической алгебре» встречается , например, в терминах «квадрат числа», «куб числа» и др.
Известно, что впервые правила преобразования уравнений, обосновав их, правда, геометрически, разработал выдающийся узбекский ученый первой половины IX в. Аль-Хорезми. В XII в. труды аль-Хорезми были переведены на латинский язык и долгое время в Европе являлись основным руководством по алгебре. Арабское название операции «восполнение» (перенесение отрицательных членов уравнения в другую часть) звучало как «ал-джебер», что и дало название разделу математики, занимающемуся решением уравнений, - «алгебра».
Начало освобождения алгебры о геометрической формы в III в. связывают с именем древнегреческого учёного Диофанта. Однако лишь после того, как французский математик Ф.Виет (1540-1603) ввел буквенные обозначения для неизвестных и известных величин, и после появления трудов Р.Декарта (1596-1650) и других европейских учёных XVI-XVII вв. процесс освобождения алгебры от геометрической терминологии был завершён. Этот процесс способствовал расцвету алгебры и развитию различных её направлений: теориям уравнений, многочленов, функций и пр.
|
|
|
Задание 1: Показать номер той пары чисел, которая является решением системы уравнений (методом подстановки):

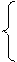
 Задание 2: Закончить составление системы, решением которой является пара чисел х=-3, у=2
Задание 2: Закончить составление системы, решением которой является пара чисел х=-3, у=2
1) х+у=….. 2) х2-у2=……
х·у=….. х+у=…..
Существует ли ещё пара чисел, удовлетворяющая данной системе?
Правило:Для решения системы двух уравнений с двумя неизвестными (методом подстановки), необходимо из одного уравнения системы выразить одно неизвестное через другое, а затем подставить полученное выражение в другое уравнение системы. Ответ записывается в виде (х;у).
Задание 3: Решить систему уравнений:
х+у=5
х·у=6
Решение:
х+у=5 х·у=6
Выразим х через у: х=5-у, подставим во 2 уравнение: (5-у)·у=6
5у-у2 –6=0
-у2+5у-6=0 : (-1)
у2-5у+6=0
а=1,b=-5, с=6
|
|
|
у1,2=  =
= 

у1= 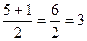 у2=
у2= 
у1=3 у2=2
х1=5-у=5-3=2 х2= 5-у =5-2=3
Ответ: (2;3), (3;2)
 Задание 4: Закончить решение
Задание 4: Закончить решение
х-у=2
х·у=8
Решение:
х-у=2 х·у=8
Выразим х через у: х=2+у, подставим во 2 уравнение: (2+у)·у=8
2у+у2 –8=0
у2+2у-8=0
у1,2=  =
= 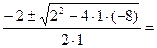
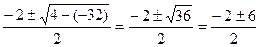
у1=  у2=
у2= 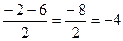
у1=2 у2=-4
х1=2+у=2+2=4 х2= 2+у =……………
Ответ: (4;2), (….;-4)
Задание 5: Решить систему и стрелками указать те пары чисел, которые будут являться решениями:
 | ||||||
 | ||||||
|
| |||||
Пример: Решить систему уравнений:
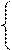 х2-у2=200
х2-у2=200
х+у=20
 Решение:
Решение:
(х-у)·(х+у)=200
х+у=20 (разделим первое уравнение системы на второе уравнение)
 , получим: х-у=10
, получим: х-у=10
х=10+у, (подставим во второе уравнение системы)
(10+у)+у=20
2у=20-10
2у=10
у=5, х=10+у=10+5=15
Ответ: (15;5)
Пример: Решить систему уравнений:
 х+х·у+у=-1
х+х·у+у=-1
х-х·у+у=3
Решение:
Сложим первое и второе уравнение системы: (х+х·у+у)+( х+х·у+у)=-1+3
х+у+х+у=2
2х+2у=2
2(х+у)=2
х+у=1, х=1-у
Подставим выражение для х в первое уравнение системы:
(1-у)+(1-у)·у+у=-1
1-у+у-у2+у=-1
-у2+у+1+1=0
-у2+у+2=0
у2-у-2=0
а=1,b=-1, с=-2
у1,2=  =
= 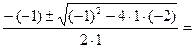
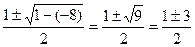
у1=  у2=
у2= 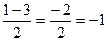
у1=2 у2=-1
х1=1-у=1-2=-1 х2= 1-у =1-(-1)=2
Ответ: (-1;2), (2;-1)
Задание 6: Решить самостоятельно :

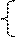
 1) х-у=6 2) х2-у2=27 3) х-х·у+у=7
1) х-у=6 2) х2-у2=27 3) х-х·у+у=7
х·у=-5 х+у=-3 х+х·у+у=5
Ответ записать в виде таблицы:
| Задание | 1 | 2 | 3 |
| Ответ |
Проверь себя!
| I .Решить систему уравнений: |
| 1. х-у=2 х2-у2=12 |
| 2. х-у=1 х∙у=6 |
| 3. log2х+log2у=log26 х2-у2=13 |
| II . Разность двух чисел в 24 раза меньше их произведения, а сумма этих чисел в 5 раз больше их разности. Найти эти числа |
Контрольная работа
Уровень А:
1) Решить иррациональное уравнение:
а) 
б) 
в) 
г) 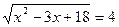
2) Решить систему уравнений:
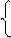
 а) х-у=3 б) х·у=-2
а) х-у=3 б) х·у=-2
х·у=10 2х+у=0
Уровень В:
1) Решить иррациональное уравнение:
а) 
б) 
2) Решить систему уравнений:

 а) х-2у=-7 б) х2-у2=9
а) х-2у=-7 б) х2-у2=9
х·у=-6 х-у=1
Уровень С:
1) Решить иррациональное уравнение:
а) 
б) 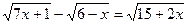
 2) Решить систему уравнений:
2) Решить систему уравнений:
х-х·у+у=-7
х+х·у+у=1
Дата добавления: 2021-12-10; просмотров: 20; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
