Тема 1. Определение и свойства степенной функции

Определение:Функцию у=х^р, где р - заданное действительное число, называют степенной функцией.

Свойство 1: Степенная функция у=х^р для любого р 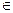R определена при х>0

Свойство 2: Множество значений степенной функции у=х^р при х>0, р≠0 – все положительные числа

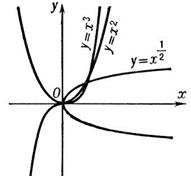
Свойство 3: Степенная функция у=х^р на интервале х>0 является возрастающей, если р>0, и убывающей, если р<0.

Задание 1:Изобразить схематично графики функций:

Тема 2. Решение иррациональных уравнений

Определение: Уравнение с одной переменной f ( x )=φ( x ) называют иррациональным, если хотя бы одна из функций φ( x ) или φ( x ) содержит переменную под знаком радикала.

Задание 1: Выбрать иррациональное уравнение:

1) 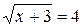4)

2) 2х+63 = 5) х²-3 х=4

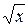3) 12- =1 6)

Задание 2: Какое из чисел –2;-1;0;1;2 будет являться корнем иррационального уравнения:

Задание 3: Является ли число х=2 корнем уравнение 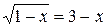, как это проверить.

Задание 4: Методом подстановки найти решение иррационального уравнения:

Правило1:Для решения иррационального уравнения необходимо возвести в степень обе части уравнения. Причём необходимо учитывать следующее:

1) если показатель корня - четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным;

2) если показатель корня - нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.

К появлению посторонних корней могут привести следующие преобразования:

-возведение в квадрат (или четную степень) обеих частей уравнения;

-умножение обеих частей уравнения на алгебраическое выражение, содержащее переменную.

Правило 2: Чтобы выяснить, имеются ли среди корней уравнения-следствия посторонние корни, необходимо проверить каждый из найденных корней подстановкой его в исходное уравнение. То есть в заключение решения обязательно выполнить проверку.

Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо эквивалентно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.

Простейшие иррациональные уравнения

Правила равносильного перехода для простейших иррациональных уравнений:

а) если a>0, то 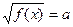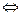f(x)=a² (здесь проверять область допустимых значений f(x) не надо, так как f(x)=a² - проверяется автоматически).

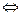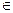б) если x Ǿ.

в) если квадратный корень равен нулю, то и подкоренное выражение равно нулю:

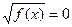
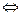f(x)=0.

Уравнения вида при n=2m решаются по аналогичным правилам.

г) если n=2m+1, то 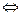f(x)=aⁿ.

Пример: Решить иррациональное равнение:

1) 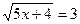2)

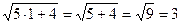
Решение: Проверка: Решение: Проверка:

а)

5х+4=9 3=3 х+4=3х-6 б)

5х=9-4 х-3х=-6-4 3=3

5х=5 -2х=-10

х=1 Ответ: х=1 х=5 Ответ: х=5

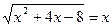
Решение: Проверка:

х²+4х-8=х² х=2

х²+4х-8-х²=0 2=2

4х-8=0

4х=0+8

4х=8

х=2 Ответ: х=2

Задание 5: Заполнить таблицу:

№	Уравнение	Возведение в квадрат	упрощение	проверка	ответ
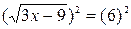
1			3х-9=36 3х=36+9 3х=45 х=15	6=6	х=15
2
3			3х+5=х+13 3х-х=13-5 2х=8 х=4		х=4
4
5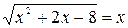

2. Уравнения с одним радикалом вида

Здесь в правой части выражение g(x) может принимать как отрицательные, так и положительные значения. Возведение в квадрат является равносильным преобразованием, если g(x) . Если g(x)<0, то уравнение решений не имеет.

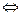
; (условие f(x) на область допустимых значений не включается в систему, оно проверяется автоматически, так как правая часть уравнения системы неотрицательна).

Задание 6: Закончить решение:

Решение:

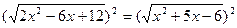
2х²-6х+12=х²+5х-6

2х²-6х+12-х²-5х+6=0

х²-11х+18=0

а=1, b=-11, с=18

х_{1,2= =}

х₁= х₂=

Проверка:

1) х₁=9

2) х₂=2

Ответ: х₁=9, х₂=….

Решение:

х²-5х+15=9

х²-5х+15-9=0

х²-5х+6=0

а=1, b=-5, с=6

х_{1,2= =}

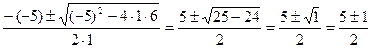
х₁= х₂=

Проверка:

…………..

Задание 7: Найти ошибку:

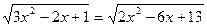
Решение:

3х²-2х+1=2х²-6х+13

3х²-2х+1-2х²+6х-13=0

х²+4х-12=0

а=1, b=4, с=-12

х_{1,2= =}

х₁= х₂=

Проверка:

3) х₁=2

4) х₂=-6 не уд.

Ответ: х₁=2

Задание 8: Выполнить:

****

***

х=5

х=2

х=1

х=11

х=3

х=6

*****

Задание 9: Найти сумму корней иррационального уравнения:

Формулы сокращенного умножения

квадрат суммы: ( а + в )² = а² + 2ав + в²

квадрат разности: ( а - в )² = а² - 2ав + в²

разность квадратов: а² - в² = ( а - в )( а + в)

куб суммы: ( а + в )³ = а³ + 3а² в + 3ав² + в³

куб разности: ( а - в )³ = а³ - 3а² в + 3ав² - в³

разность кубов: а³ - в³ = ( а – в)( а² + ав + в² )

сумма кубов: а³ + в³ = ( а + в)( а² - ав + в² )

Задание 10: Заполнить таблицу:

№	многочлен	формула	упрощение	результат
1	(2х+3)²	Квадрат суммы	(2х)² + 2·2х·3 + 3²	4х²+12х+9
2	(4х-1)²
3	(2х-2)³
4	(х+5)³
5	(х+6)²

Пример: Решить иррациональное уравнение:

х-6 =

Решение:

(х-6)² =( )²

(х)²-2·х·6+6²=2х+12

х²-12х+36=2х+12

х²-12х+36-2х-12=0

х²-14х+24=0

а=1, b=-14, с=24

х_1,2==

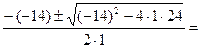
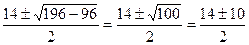
х₁= 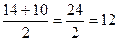х₂=

Проверка:

1) х₁=12 2) х₂=2- не уд

12-6=6 2-6 =-4

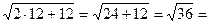6 4

6=6 -4≠4

Ответ: х=12

Задание 11: Проверить решение и найти ошибку:

х+1 =

Решение:

(х+1)² =( )²

(х)²+2·х·1+1²=-1-х

х²+2х+1=-1-х

х²+2х+1+1+х=0

х²+3х+2=0

а=1, b=3, с=2

х_1,2==

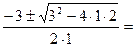
х₁= 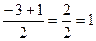х₂=

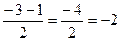
Проверка:

1) х₁=1 – не уд 2) х₂=-2

1+1=2 -2+1=1

( по определению , а≥0 )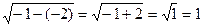

1=1

Ответ: х=-2

Задание 12: Решить иррациональное уравнение:

2) х-2 =

3) х+3 =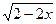

Задание 13: Найти сумму корней иррационального уравнения:

1) 2) х+4 =

а) 4 б) 5 в)6

3. Уравнения с одним радикалом вида

Уравнение вида равносильно уравнению без радикала f(x)=g³(x).

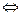f(x)=g³(x).

4. Уравнение вида

Часто встречаются иррациональные уравнения вида (или приводятся к такому виду разложением на множители) . Это уравнение равносильно совокупности двух систем:

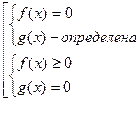, или системе: .

Пример. Решить уравнение: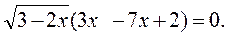

Решение:

Произведение равно нулю тогда и только тогда, когда хотя бы из сомножителей равен нулю, а другие при этом имеют смысл.

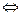
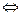
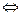
Ответ: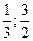

Методы замены переменных

Еще одним часто встречающимся методом преобразования уравнения является метод замены переменных. Для уравнений этот метод состоит в следующем: данное уравнение приводят к виду g(f(x))=0, где z=g(f(x)) – сложная функция, являющаяся композицией двух функций y=f(x) и z=g(y). Если y=y₁; y=y₂;…y=y_n;

все корни уравнения g(x)=0,

f(x)=y₁

f(x)=y₂

то g(f(x))=0 …….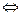

f(x)=y_n

Дата добавления: 2021-12-10; просмотров: 121; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!