Способ построения доверительных границ и интервалов

Для построения доверительного интервала (или границы) необходимо знать закон распределения статистики z = z( x₁, ξ₂... x _n), по которой оценивается неизвестный параметр (такой статистикой могут быть сама оценка â(x₁, ξ₂...x_n), статистика, от которой зависит оценка â, достаточная статистика или статистика, близкая к достаточной).

Один из способов построения состоит в следующем (проследим логику рассмотренного примера).

1) Построим случайную величину j = j(z, a), зависящую от статистики z и неизвестного параметра a таким образом, что:

— закон распределения для j известен и не зависит от a;

— j(z, a) непрерывна и монотонна по а.

Такая случайная величина j(z, a) называется центральной статистикой.

     2) Выберем интервал (f₁, f₂) для j так, чтобы попадание в него случайной величины j было практически достоверным (с вероятностью P_Д):

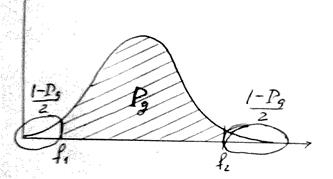P{f₁ <j(z, a) < f₂}= P_Д,       (9)  

для чего достаточно в качестве f₁ и f₂ взять квантили распределения для j уровня (1-Р_Д)/2 и (1+Р_Д)/2 соответственно (рис. 6).

3) Перейдем в (9) к другой записи случайного события, разрешив неравенства относительно параметра a.

Рис. 6. Выбор интервалов

Предполагая монотонное возрастание j по а получим:

P{g(z, f₁)< a < g(z, f₂)} = P_Д.

Это соотношение верно при любом значении параметра a (поскольку это так для (9)), и потому, согласно определению, интервал со случайными концами (g(z, f₁), g(z, f₂)) является доверительным для a с уровнем доверия Р_Д.

Если имеем монотонное убывание j по а, интервалом будет

(g(z, f₂), g(z, f₁)).

Замечания.

1. сделанное выше предположение о монотонности j(z, a) по а, не является существенным. В случае, если монотонности нет,

 Рис. 7. Доверительное множество при отсутствии монотонности

результатом разрешения неравенств в (9) под знаком вероятности относительно параметра a является не интервал, а более сложное доверительное множество, например, два интервала (рис. 7).

2. Если требуется построить одностороннюю доверительную границу (верхнюю или нижнюю), нужно использовать только одно из неравенств под знаком вероятности в (9). Используем

или P{j(z, a) > f₁} = P_Д, f₁=Q(1 - P_Д),

                          или     P{j(z, a) < f₂} = P_Д ,  f₂ = Q(P_Д),

согласовав знак неравенства с характером монотонности j по а (возрастание или убывание) и с характером границы (верхняя или нижняя). В неравенствах обозначено Q( P) — квантиль уровня P. После разрешения неравенства под знаком P получим односторонние доверительные границы для a.

3. О числовых значениях интервала. После применения формул для интервала, например, (8), к конкретным наблюдениям мы получаем конкретный интервал, например, для n = 9, при s = 1, Р_Д= 0,95 (соответствующее значение f_P = 1,96) и 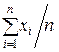= 3,87 получаем по (8)

a₁ = 3,22, a₂ = 4,52.

Смысл замечания состоит в том, что нельзя писать аналогично соотношению (6)

,

поскольку под знаком вероятности нет случайного события. Параметр а не является случайной величиной, и интервал (3,22, 4,52) тоже не случайный, в отличие от формулы (6), где интервал является случайным. Коэффициент доверия Р_Д= 0,95 — это характеристика способа определения интервала, но не конкретного полученного интервала.

4. О точности интервального оценивания (о ширине интервала (6)).

                                                             (6)

а) Ошибка оценивания d, в соответствии с (6),

d=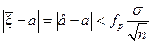

не превосходит значения 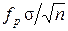 с вероятностью Р_Д < 1. При массовых вычислениях подобного рода точность не хуже  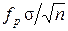в числе случаев, доля которых Р_Д. Уровень доверия Р_Дозначает, что правило определения интервала дает верный результат с вероятностью Р_Д, которая обычно близка к единице, однако, единице не равна.

б) Хотелось бы иметь высокую точность с высокой вероятностью. Однако, при увеличении Р_Д значение f_p тоже увеличивается, так что с высокой вероятностью можно гарантировать относительно низкую точность —чем надежнее гарантия, тем меньше она гарантирует.

в) Связь точности с s и n: чем меньше s, тем выше точность. Увеличение n также улучшает точность, которая изменяется как 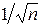. Чтобы повысить точность в 3 раза, нужно число наблюдений увеличить в 9 раз.

6.4. Интервалы для параметров нормального распределения

А. Распределение хи-квадрат c k степенями свободы. Для рассмотрения типичных практических примеров потребуются сведения о некоторых распределениях. Многие задачи статистики связаны с распределением хи-квадрат (χ²(k)).

Пусть a₁, a₂…a_k — независимые случайные величины, распределенные по стандартному нормальному закону N(0,1). Рассмотрим сумму их квадратов и обозначим соответствующую случайную величину через :

.                                      (10)

Распределение этой случайной величины называют распределением хи-квадрат с k степенями свободы. Нетрудно показать (см., например, [2], §24), что плотность этого распределения выражается следующей формулой:

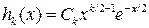, x > 0,                                 (11)

где С _k = 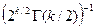 — нормирующий множитель,  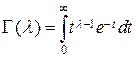— гамма-функция. На рис. 8 показаны графики при различных значениях k.

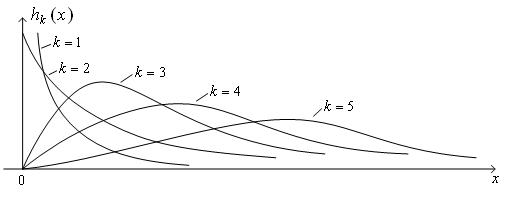
Рис. 8. Семейство плотностей распределения χ²

Заметим, что при k = 2 получаем показательное распределение:

.

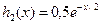Из соотношения (10) получаем первые два момента:

M  = k,   D  = 2k, (проверить!)

откуда ясно, что с увеличением числа k степеней свободы распределение c²(k) смещается вправо и расплывается, а также, что оно асимптотически нормально (в силу центральной предельной теоремы):

c²(k) ~ N(k, 2k) при k®¥;

при k > 30 можно пользоваться таблицами нормального распределения.

Далее отметим весьма полезные сведения.

Замечание. Это распределение c² является частным случаем гамма-распределения, для которого плотность выражается формулой

p(x; l, a) = C(l, a) , x >0, l > 0, a > 0,

где C(l, a) = - нормирующий множитель; l – параметр формы, a – параметр масштаба, 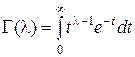 - известная гамма-функция. Первые два момента m₁ и s² равны соответственно

m₁ = l/a, s² = l/a².

Характеристическая функция f( t) этого распределения выражается формулой:

f( t) 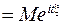 =  = = . (12)

Если l — целое число, то распределение называется распределением Эрланга, которому подчиняется сумма l независимых случайных величин, показательно распределенных с плотностью .

Справедливость формулы (11) можно легко показать, определив характеристические функции для a₁² и затем для . характеристическая функция для случайной величины  оказывается равной

(1–2it)^-k/2,

откуда следует, что соответствующее распределение является гамма-распределением с параметрами l = k/2, a = 1/2.

 

---

Дата добавления: 2021-12-10; просмотров: 32; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!