Часть 2. Интервальное оценивание
Лекция 5
Метод порядковых статистик.
В статистике, кромесистемы моментов, в качестве числовых характеристик распределений широко используются числовые характеристики, называемые квантилями.
Определение. Значение xp случайной величины x называется p-квантилью, если
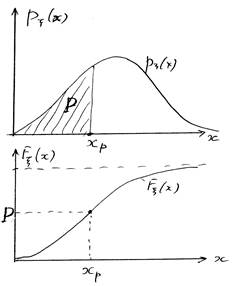 P{x< xp} = p,
P{x< xp} = p,
где xp — это корень уравнения
Fx(xp) = p , (рис. 3).
Примеры р-квантили:
x0,5 — медиана — характеристика среднего значения случайной величины;
Рис. 3. Графическая иллюстрация квантили xp
x0,98 — максимальное, с вероятностью 0,98, значение случайной величины, т.к. P{x < x0,98} = 0,98;
x0,02 — минимальное, значение случайной величины, т.к. P{x ³ x0,02 } = 1 – P{x < x0,02 } = 1– 0.02 = 0,98;
x3/4 и x1/4 — верхняя и нижняя квартили; их разность(x0,75 – x0,25) — межквартильная широта — служит характеристикой разброса.
Оценка p-квантилей . Неизвестные p-квантили легко оцениваются по выборке. Действительно, пусть
x1, х2...xn —выборка, результаты n независимых наблюдений над случайной величиной x с функцией распределения F(x). Упорядочив их по возрастанию, получаем вариационный ряд
x(1) £ x(2) £ ... £ x(n).
Чтобы подчеркнуть случайность ряда, запишем его греческими символами
x (1) £x (2) £ ... £ x(n).
член вариационного ряда x (i) с номером i (заметим, что это случайная величина) называется i-й порядковой статистикой. по вариационному ряду построим функцию
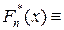
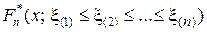
эмпирического распределения, и, согласно общему принципу о том, что выборочные характеристики являются состоятельными оценками характеристик распределения генеральной совокупности, рассмотрим в качестве оценкидля p-квантили xp выборочную квантиль z p, т.е. корень уравнения
|
|
|
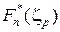 = p. (8)
= p. (8)
Поскольку  — функция кусочно-постоянная, то корнем является одна из порядковых статистик zp = x([np]+1), (9)
— функция кусочно-постоянная, то корнем является одна из порядковых статистик zp = x([np]+1), (9)
с номером  = [np]+1, т.е. целая часть числа np плюс 1(рис. 4).
= [np]+1, т.е. целая часть числа np плюс 1(рис. 4).
 Нетрудно показать, что zp является состоятельной оценкой для xp:
Нетрудно показать, что zp является состоятельной оценкой для xp:

Кроме того, известна
теорема Крамера, которая гласит: для непрерывных распределений с плотностью q(x) оценка zp асимптотически нормальна с параметрами: Mzp = xp, Dzp = 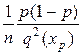 . (10)
. (10)
Рис. 4. Графическая иллюстрация выборочной квантили
Метод оценки параметров основан на оценках zp при разных p . Как в методе моментов? параметры выражаем через моменты, а затем моменты заменяем выборочными моментами. Аналогично в методе порядковых статистик: параметры выражаем через квантили, а затем квантили заменяем выборочными квантилями, т.е. порядковыми статистиками.
Пусть x1, x2…xn — выборка с функцией распределения F(x;a), зависящей от параметра a, значение которого требуется оценить. Выберем р так, чтобы квантиль xр зависела от параметра:
|
|
|
xр = f(a).
Выразим параметр а через квантиль xр:
а = g(xр),
и вместо xр подставим выборочную квантиль zp = x([np]+1), в результате чего получим состоятельную оценку
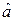 = g(x ([np]+1)).
= g(x ([np]+1)).
Таким же образом можно построить оценки и для неодномерного параметра.
Основное и очень важное преимущество оценок, основанных на порядковых статистиках, — их устойчивость к засорению наблюдений и к изменениям закона распределения.
Примеры оценок параметров нормального распределения.Пусть x1, x2…xn — выборка из нормальной совокупности N(m, s2).
1) Оценка среднего m . Известно или нет значение s — безразлично. В силу симметрии нормального распределения параметр m является медианой, т.е. квантилью уровня ½,
m= x½
и потому может быть оценен выборочной медианой:
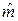 = z½ = x([n/2]+1).
= z½ = x([n/2]+1).
Можно сравнить по точности эту оценку с эффективной оценкой

для которой дисперсия 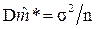 .
.
согласно (10), теореме Крамера, D 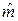 »
»  ,
,
т.е. очень простая и устойчивая к засорению оценка 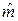 уступает по точности оценке
уступает по точности оценке  в
в 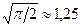 раза, т.е. 25 %.
раза, т.е. 25 %.
2) Оценка стандартного уклонения s.
Легко проверить, что верхняя и нижняя квартили равны соответственно
|
|
|
x3/4 = m + 0,675s и x1/4= m – 0,675s,
т.к . 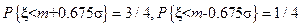
И потому
s = (x3/4 - x1/4) / 1,35,
и потому оценивать s можно следующим образом:
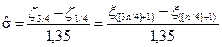 .
.
3) Оценка стандартного уклонения s по размаху.
Пусть x (1) и x (n) — минимальный и максимальный член выборки, разность которых называется размахом w:
w = x (n) – x (1).
Ясно, что
Mw = c(n)s,
и потому оценкой для s может служить
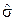 = w/c(n) = k(n)w,
= w/c(n) = k(n)w,
где k(n) берем из статистических таблиц [4]. Ниже приведены значения коэффициента k(n)и коэффициента эффективности
e ff = 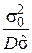 , где
, где  — нижняя граница Рао-Крамера,
— нижняя граница Рао-Крамера,
а также потеря точности:
(1– 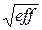 ) ∙ 100,
) ∙ 100,
измеряемая в процентах, по сравнению с нижней границей Рао-Крамера.
Табл. 1. Значение коэффициентов k и n
| n | 2 | 5 | 10 |
| k(n) | 0,866 | 0,430 | 0,325 |
| eff | 1,000 | 0,955 | 0,855 |
потеря точности, (1 – 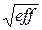 )100, % )100, %
| 0 | 2,5 | 7 |
Для устойчивости оценки к засорению используют подразмахи wm порядка m , где m = 1, 2, 3…:
wm = x (n- m +1) - x (m),
так что оценка имеет вид:
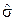 = k m(n) w m.
= k m(n) w m.
Значение коэффициента k m(n) берется из таблиц.
4) Распределение порядковых статистик . При анализе оценок, получаемых рассматриваемым методом, необходимо знать распределения порядковых статистик. Если распределение одного наблюдения x непрерывно с плотностью p(x) = F ’(x), топлотность распределения для k-й порядковой статистики x (k) выражается следующей формулой:
|
|
|
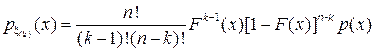 ,
,
которая получается вычислением вероятности события
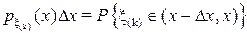 ,
,
по полиномиальной схеме. Событие означает, что при n-кратном испытании случайной величины x
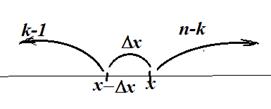
событие 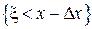 , вероятность которого
, вероятность которого 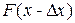 , появится (k-1) раз: множитель
, появится (k-1) раз: множитель 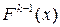 ,
,
событие  , вероятность которого (
, вероятность которого ( 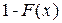 ), появится (n-k) раз: множитель
), появится (n-k) раз: множитель 
и событие 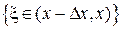 , вероятность которого
, вероятность которого 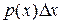 , появится 1 раз: множитель
, появится 1 раз: множитель 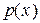 .
.
Часть 2. Интервальное оценивание
Дата добавления: 2021-12-10; просмотров: 64; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
