Доверительные границы и интервалы

 

результатом применения оценки â(x₁, х₂...x _n) является одно числовое значение, которое не дает представления о точности, т.е. о том, насколько близко полученное значение к истинному значению параметра. Интуитивно ясно, что такое представление может дать, например, дисперсия оценки, так что истинное значение неизвестного должно находиться где-то в пределах

â ± (2¸4)  

Внесем уточнения того, что мы хотим.

 

Определения

Пусть ξ ≡ (x₁, ξ₂...x_n) —выборка, т.е. n независимых наблюдений над случайной величиной с функцией распределения F(x;a), зависящей от параметра a, значение которого неизвестно.

Определение 1. Интервал I(x) = (a₁(x), a₂(x)) со случайными концами (случайный интервал), определяемый двумя функциями наблюдений, называется доверительным интервалом для параметра a с уровнем доверия Р_Д (обычно близким к 1), если

P{I(x) ' a} º P{a₁(x)< a < a₂(x)} = P_Д,               (1)

т.е. если при любом значении параметра a минимальная вероятность (зависящая от a) накрыть случайным интервалом I(x) истинное значение a велика (не менее Р_Д), и равна P_Д.

Определение 2. Функция наблюдений â_н(x₁, ξ₂... x_n) (случайная величина), называется нижней доверительной границей для параметра a с уровнем доверия Р_Д (близким к 1), если

P{â_н(x₁, ξ₂... x_n)< a}= P_Д.                                     (2)

Т.е. если при любом значении параметра a минимальная вероятность события {â_н(x) < a} велика (не меньше P_Д),  и равна P_Д.

Определение 3. Функция наблюдений â_в(x₁, ξ₂... x_n) (случайная величина) называется верхней доверительной границей для параметра a с уровнем доверия Р_Д, если

P{â_в(x₁, ξ₂... x_n)> a}= P_Д .                             (3)

Т.е. если при любом значении параметра a минимальная вероятность события {â_в(x) > a} велика (не меньше P_Д), и равна P_Д.

Вероятность Р_Д называют также доверительной вероятностью.

Пример. Доверительный интервал для среднего нормальной совокупности при известной дисперсии

Пусть x = (x₁, ξ₂...x_n) — выборка из нормальной N(a, σ²)совокупности. Достаточной оценкой для а является

â = â(x₁,ξ₂…x_n) = 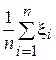º`x,

распределенная по нормальному закону N(a, ). Пронормируем её, образовав случайную величину      

,                                               (4)

которая распределена нормально N(0,1) при любом значении а.

По заданному уровню доверия Р_Д (рис. 5) определим для j симметричный  интервал (-f _p , f _p) так, чтобы он содержал в себе вероятность Р_Д, т.е.

.                                              (5)

Ясно, что f _p есть квантиль порядка (1 + Р_Д) / 2 стандартного нормального распределения N(0,1). Заметим, что j  зависит от а, и (5) верно при любом значении а.

Рис. 5. Выбор интервала при нормальном распределении

 

Подставим в (5) выражение для j из(4) и разрешим неравенство под знакомвероятности в (5) относительно а. получим соотношение

                                                             (6)

верное по-прежнему при любом значении а. под знаком вероятности слева и справа имеем две функции наблюдений

и ,                 (7)

определяющие случайный интервал

I(x₁, ξ₂ ...x_n) = ( ,),                                (8)

который в силу (6) накрывает неизвестное значение параметра а с большой вероятностью, равной Р_Д, при любом значении параметра а, и потому, по определению  доверительного интервала, он является доверительным для а с уровнем доверия Р_Д.

 

---

Дата добавления: 2021-12-10; просмотров: 22; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!