Выпуклость графика функции. Точки перегиба

Определение 1. Функция f называется выпуклой внизна интервале (a , b) или просто выпуклой, если график функции лежит над касательной в любой точке данного интервала.

Определение 2. Функция f называется выпуклой вверхна интервале (a , b) или просто вогнутой, если график функции лежит под касательной в любой точке данного интервала.

Определение 3. Точки x₀ области определения функции f называется точками перегиба для функции f , если в этих точках график функции f меняет свою выпуклость на противоположную.

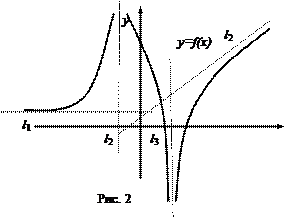
Функция y = f(x), изображенная на рисунке 2 выпукла вверх (вогнута) на интервалах (х₁, х₂), (х₃, х₄), выпукла вниз (выпукла) на интервале (х₂, х₃), точки х₂, х₃ являются точками перегиба графика функции f.

Если х₀ произвольная фиксированная точка интервала (a , b) и

,

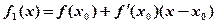то уравнение касательной к графику функции y = f(x) в точке (х₀ , f(х₀)) задается формулой y = f₁(x). Тогда по определению получаем:

если функция f(х) выпукла вниз на интервале (a , b), то для любого x Î (a , b) имеем f(х) ³ f₁(x) ;

если функция f(х) выпукла вверх на интервале (a , b), то для любого x Î (a , b)имеем f(х) £ f₁(x).

Теорема 1 (второе достаточное условие выпуклости функции). Пусть функция f дважды дифференцируема на интервале (a , b). Тогда:

1) если f '' ( x ) ³ 0 на ( a , b ), то функция f выпукла вниз на интервале ( a , b );

2) если f '' ( x ) £ 0 на ( a , b ), то функция f выпукла вверх на интервале ( a , b )

Теорема 2. Если f '' (x₀) < 0 и f '' (x) непрерывна в точке x₀, то существует d-окрестность точки x₀,, в которой функция выпукла вверх.

Если f '' (x₀) > 0 и f '' (x) непрерывна в точке x₀, то существует d-окрестность точки x₀,, в которой функция выпукла вниз.

Определение 1. Точка x₀ области определения функции f называется точкой перегиба графика функции ( или просто функции) f , если в этой точке график функции f меняет свою выпуклость на противоположную, т. е. существует такая проколотая окрестность точки x₀, что в левой и правой полуокрестностях точки x₀ функция f имеет разную выпуклость.

Лемма 1. Пусть функция f имеет производную в d -окрестности точки x ₀ , причем эта производная непрерывна в точке . Тогда,

1) если на интервале ( x ₀ , x ₀ + d ) функция f выпукла вверх (вниз), то всюду в пределах интервала ( x ₀ , x ₀ + d ) график функции лежит не ниже (не выше) касательной к графику, проведенной в точке M ( x ₀ , f ( x ₀ )).

2) если на интервале ( x ₀ - d , x ₀ ) функция f выпукла вверх (вниз), то всюду в пределах интервала ( x ₀ - d , x ₀ ) график функции лежит не выше (не ниже) касательной к графику, проведенной в точке M ( x ₀ , f ( x ₀ )).

Лемма 2. Пусть функция f имеет производную в некоторой окрестности точки x ₀ , причем эта производная непрерывна в точке x ₀ . Тогда, если x ₀ точка перегиба графика функция f , то существует такая d -окрестность точки x ₀ , что график функции f слева и справа от точки x ₀ лежит по разные стороны от касательной, проведенной к графику функции f через точку M ( x ₀ , f ( x ₀ )).

Теорема 1 (необходимое условие точки перегиба графика функции). Если в точке x₀ функция f имеет вторую производную  f '' (x₀) и точка x₀ является точкой перегиба графика функции f , то f '' (x₀)=0.

Теорема 2 (первое достаточное условие точки перегиба графика функции). Пусть функция f дважды дифференцируема в некоторой окрестности точки x₀. и f '' (x₀) = 0 . Тогда, если в пределах этой окрестности вторая производная f '' (x) имеет разные знаки слева и справа от точки x₀,, то точка x₀ является точкой перегиба графика функции f .

Замечание. Условие равенства f '' (x₀) = 0 значения второй производной функции f в точке x₀ нулю не является достаточным для того, чтобы точка стала точкой перегиба графика функции f. Например, для функции f (x) = x⁴ имеем

f '' (x) = 12x² , f '' (0) = 0, но точка x = 0 не является точкой перегиба функции f (x) = x⁴. 

Теорема 3 (второе достаточное условие точки перегиба графика функции). Пусть функция f трижды дифференцируема в точке x₀. и f '' (x₀) = 0, f ''' (x₀) ¹ 0. Тогда, если в пределах этой окрестности вторая производная f '' (x) имеет разные знаки слева и справа от точки x₀, то точка x₀ является точкой перегиба графика функции f .

Алгоритм нахождения точек перегиба графика функцииf ;

1. найти область определения функции f;

2. вычислить первую и вторую производные функции f;

3. найти все критические точки первой производной f ' , т.е. такие точки, в которых вторая производная или не существует или обращается в ноль.

4. найти знаки второй производной на каждом из промежутках области определения, где нет критических точек.

Далее можно воспользоваться теоремой 2; если при переходе через критическую точку x₀ производной вторая производная функции f меняет свой знак, то точка x₀ - точка перегиба графика функции f.

Асимптоты функции.

Определение 1. Прямая x = a на плоскости Oxy называется вертикальной асимптотой графика функции f, если хотя бы один из пределов

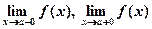
равен ±¥ .

Пример. Для функции 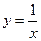 прямая x = 0 является вертикальной асимптотой.

Определение 2. Прямая y = kx + b на плоскости Oxy называется наклонной асимптотой графика функции f при x®+¥ (или просто функции), если

.

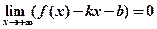Прямая y = kx + b на плоскости Oxy называется наклонной асимптотой графика функции f при x® -¥ (или просто функции), если

.

Пример 1. График функции, изображенный на рис.2 имеет две вертикальные и две наклонные асимптоты.

Теорема 1. Прямая y = kx + b является наклонной асимптотой графика функции f при x®-¥ тогда и только тогда, когда существуют два предела:

1) ,

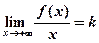2) 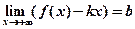. Замечание. Аналогичное утверждение имеет место и для наклонных асимптот при x® -¥.

Алгоритм нахождения асимптот графика функции f :

1) найти точки все конечные граничные точки области определения функции f;

2) вычислить правый и левый пределы функции f в каждой конечные граничной точке a области определения функции f, если хотя бы один из пределов равен ±¥ , то прямая x = a вертикальная асимптота функции f.;

3) найти пределы 1) и 2) в теореме 1 при x® +¥ (x® -¥);

4) если хотя бы один из пределов 1), 2) при x® +¥ не существует, то наклонной асимптоты при x® +¥ нет, если оба предела существуют то прямая y = kx + b наклонная асимптота при x® +¥ ;

5) если хотя бы один из пределов 1), 2) при x® -¥ не существует, то наклонной асимптоты при x® -¥ нет, если оба предела существуют то прямая y = kx + b наклонная асимптота при x® -¥ ;

---

Дата добавления: 2021-12-10; просмотров: 22; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!