Восстановить исходные значения

Служит для восстановления исходных значений изменяемых ячеек табличной модели.

Отчеты

Служит для указания типа отчета, размещаемого на отдельном листе книги. Для вывода нужных отчетов надо щелкнуть мышью их названия.

Результаты. Используется для создания отчета, состоящего из целевой ячейки и списка изменяемых ячеек модели (переменных задачи), их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.

Устойчивость. Используется для создания отчета, содержащего сведения о чувствительности решения к малым изменениям в формуле целевой функции (поле Установить целевую ячейку, диалоговое окно Поиск решения) или в формулах ограничений. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. В случае нелинейных моделей отчет содержит данные для градиентов и множителей Лагранжа.

Пределы. Используется для создания отчета, состоящего из целевой ячейки и списка изменяемых ячеек модели, их значений, а также нижних и верхних границ. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать изменяемая ячейка, в то время как значения остальных изменяемых ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение.

Сохранить сценарий

Служит для отображения диалогового окна Сохранение сценария, в котором можно сохранить сценарий решения задачи, чтобы использовать его в дальнейшем с помощью диспетчера сценариев Microsoft Excel.

Вернемся к задаче о производстве компьютерных столов. Если в диалоговом окне Результаты поиска решения (рис. 6) был отмечен первый пункт Сохранить найденное решение, то исходная таблица с электронной моделью задачи примет вид

Рис. 7.

Изменившиеся ячейки выделены серым фоном.

Перед листом с электронной моделью появятся листы с выбранными отчетами. Содержимое отчетов можно редактировать также как любые данные электронной таблицы – изменять формат ячеек, размер шрифта, корректировать имена ячеек. Рассмотрим все отчеты подробнее.

Отчет по результатам

Отчет состоит из трех таблиц, расположенных на одном листе книги Excel (рис. 8).

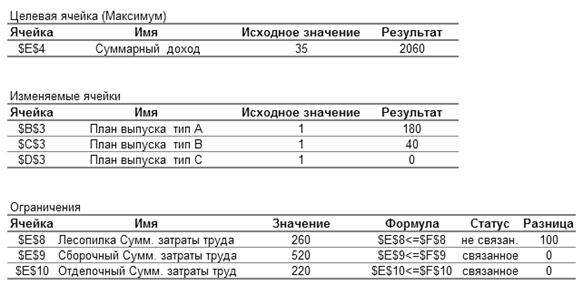
Рис. 8.

В первой таблице выводятся сведения о целевой функции. В столбце Исходное значение приведено значение целевой функции до начала вычислений, в столбце Результат – после оптимизации.

Следующая таблица содержит значения искомых переменных (изменяемых ячеек) до и после решения задачи.

Последняя таблица показывает значения левых частей ограничений на оптимальном решении задачи. В столбце Формула приведены зависимости, которые были введены в диалоговом окне Поиск решения, в столбце Разница показано количество неиспользованного ресурса. Если ресурс дефицитен, т.е. используется полностью, то в столбце Статус указывается связанное (соответствующее ограничение активно); при неполном использовании ресурса в этом столбце указывается не связанное (ограничение не активно).

Из отчета по результатам применительно к нашей задаче видим, что оптимальный план производства состоит в еженедельном выпуске 180 столов типа А и 40 столов типа В, а столы вида С выпускать не выгодно. Таким образом , и максимальный суммарный доход долл. При этом трудовые ресурсы в сборочном и отделочном цехах используются полностью, т.е. являются дефицитными, а на лесопилке наблюдается избыток трудоресурсов в объеме 100 чел.-час. в неделю.

Отчет по устойчивости

Отчет по устойчивости содержит информацию, позволяющую провести постоптимальный анализ решения задачи. Цель анализа заключается в определении таких границ изменения исходных данных задачи (коэффициентов целевой функции и правых частей ограничений), при которых ранее найденный оптимальный план сохраняет свою оптимальность и в изменившихся условиях.

Отчет состоит из двух таблиц, изображенных на рисунке 9.

Рис. 9.

В первой таблице (Изменяемые ячейки) приводится следующая информация о переменных:

· результирующее значение– оптимальные значения переменных;

· нормированная стоимость – ее величина равна значению соответствующей симплексной оценки с противоположным знаком. Для невыпускаемой продукции нормированная стоимость показывает, на сколько изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

· коэффициенты целевой функции;

· предельные значения приращения коэффициентов целевой функции, которые показывают на сколько можно увеличить и уменьшить каждый целевой коэффициент в отдельности, сохраняя при этом оптимальные значения переменных.

Во второй таблице (ограничения) приводятся аналогичные значения для ограничений задачи:

· величины использованных ресурсов (левые части ограничений) при оптимальном плане выпуска продукции;

· теневые цены, т.е. оптимальные значения двойственных переменных, которые показывают, как изменится целевая функция при изменении соответствующего запаса ресурса на единицу;

· исходные запасы ресурсов (правые части ограничений);

· предельные значения приращений ресурсов (их допустимое увеличение и уменьшение), при которых сохраняется оптимальный план двойственной задачи и базисный набор переменных, входящих в оптимальное решение исходной задачи (ассортимент выпускаемой продукции).

Используем результаты отчета по устойчивости для проведения постоптимального анализа в нашей задаче:

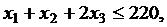
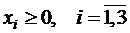Исследуем сначала влияние на оптимальный план изменений коэффициентов целевой функции – цен реализации продукции.

Из первой таблицы следует, что оптимальный план производства компьютерных столов не изменится, если первоначальная цена долл. стола типа А возрастет на 2 доллара или уменьшится на 0,333 доллара. Другими словами, условие сохранения оптимального плана при изменении цены стола А имеет вид: , т.е. .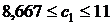

Аналогично, условие сохранения оптимального плана при изменении цены стола В имеет вид: или .

Наконец, при изменении цены стола типа С ранее найденный план останется оптимальным, если исходная цена 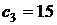возрастет не более чем на 1 доллар. В то же время любое уменьшение цены не влияет на оптимальный план , так как число равно , т.е. практически является бесконечно большим числом. Таким образом, условие сохранения оптимальности плана при изменении цены примет вид . Это означает, что столы вида С не выгодно выпускать ( ), если цена на них будет не выше 16 долларов. Если же цена превысит 16 долларов за стол, то план перестанет быть оптимальным, и в новом оптимальном решении 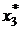будет положительным т.е. производство столов типа С станет выгодным.

Оценим теперь влияние на оптимальный план изменений правых частей ограничений – запасов трудовых ресурсов на разных производственных участках. Интерпретация данных второй таблицы отчета зависит от того, является ли исследуемое ограничение связанным (активным), или не связанным. Если ограничение не связанное, то соответствующий ему ресурс недефицитен и уменьшение его запаса на величину, не превышающую избытка, не влияет на план выпуска . Тем более не изменяет оптимальный план увеличение запаса недефицитного ресурса, приводя только к возрастанию неизрасходованного остатка. Если же ограничение - связанное, т.е. соответствующий ресурс дефицитен и расходуется полностью, то любое изменение его запаса изменяет объем выпускаемой продукции. Единственное, что можно определить в данном случае, это диапазон изменения запаса ресурса, гарантирующий сохранение прежнего ассортимента выпускаемой продукции.

О дефицитности ресурса можно судить либо по статусу ограничения в третьей таблице отчета о результатах, либо по значению теневой цены из второй таблицы отчета по устойчивости – дефицитный ресурс имеет положительную теневую цену, а недефицитный – нулевую.

Из первой строки второй таблицы видим, что на лесопилке трудоресурсы избыточны, так как их теневая цена . Следовательно, оптимальный план выпуска продукции не изменится, если запас трудовых ресурсов 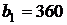уменьшится на величину избытка в 100 чел.-час., или увеличится на любое сколь угодно большое число. Таким образом, условие сохранения оптимального плана при изменении объема трудоресурсов на лесопилке имеет вид: .

Во второй и третьей строках таблицы теневые цены положительны, значит трудоресурсы в сборочном и отделочном цехах дефицитны – при оптимальных объемах производства используются полностью. Следовательно, любое изменение их количества приведет к изменению оптимального плана . В этом случае числа из столбцов Допустимое увеличениеиДопустимое уменьшениедают границы изменения запасов ресурса, обеспечивающие сохранение прежнего состава базисных (положительных) переменных оптимального плана – ассортимента выпуска продукции.

Итак, при изменении объемов ресурсов в сборочном цехе в пределах , т.е. при ассортимент выпуска не изменится.

Аналогично, если объем трудоресурсов в отделочном цехе будет находится в пределах , т.е. при , то ассортимент выпуска не изменится.

На экономическом языке это означает, что если запасы ресурсов изменяются в указанных пределах, то по оптимальному плану по-прежнему надо выпускать только столы типа А и В, но уже в новых объемах.

Напомним, что теневая цена ресурса численно равна изменению оптимального значения целевой функции при увеличении (уменьшении) запаса данного ресурса на единицу. Как видно из таблицы, теневая цена трудоресурса в сборочном цехе , а в отделочном цехе . Условие сохранения теневых цен (оптимальных значений двойственных переменных 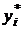) совпадает с условиями сохранения базиса оптимального плана. Следовательно, привлечение одной дополнительной единицы ресурса в сборочный цех приведет к увеличению суммарного дохода на 1 доллар, а одна дополнительная единица ресурса в отделочном цехе увеличит суммарный доход на 7 долларов. Отсюда ясно, что если появится возможность вовлечь в производство дополнительные ресурсы в количестве, например, 30 человеко-часов, то направить их надо в отделочный цех, так как это увеличит прибыль на долларов. Заметим, что при этом оптимальный план производства компьютерных столов изменится, но сохранится его структура – ассортимент выпускаемой продукции.

Отчет по пределам

Третий отчет для нашей задачи, называемый отчетом по пределам, состоит из двух таблиц (рис.10).

Первая таблица в комментариях не нуждается.

Рис.10.

Во второй таблице показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального плана выпуска:

· приводятся значения в оптимальном решении;

· приводятся нижние и верхние пределы изменения значений и значения целевой функции при выпуске данного типа продукции на нижнем и верхнем пределах.

Так например, если из оптимального плана исключить выпуск столов типа А, положив 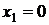и сохранить оптимальные значения остальных переменных, то доход от реализации продукции будет равен

Значения целевой функции – дохода от реализации продукции, вошедшей в оптимальное решение на верхних пределах везде равно максимальной величине 2060 долларов.

Рассмотренный пример показывает, как использование средства «Поиск решения» облегчает задачу принятия оптимальных решений в экономике.

Рекомендуемая литература

Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: BHV – Санкт-Петербург, 1997. – 384 с.
Карлберг К. Бизнес-анализ с помощью Microsoft Excel. – М.-СПб -Киев: Издательский дом «Вильямс», 2002. – 448 с.
Ларсен Р. У. Инженерные расчеты в Excel. – М.: Диалектика-Вильямс, 2003. – 544 с.
Хазанова Л. Э. Математические методы в экономике. – М.: Издательство БЕК, 2002. – 144 с.

Приложение 1

Дата добавления: 2018-02-15; просмотров: 634; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!