Подготовка задачи к решению в MS Excel

Стр 1 из 4Следующая ⇒

Министерство образования Российской Федерации

БАЙКАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЭКОНОМИКИ И ПРАВА

Тарасенко Н.В.

Шеломенцева Н.Н.

МАТЕМАТИКА-2

Решение задач оптимизации в Excel

Методические указания

для студентов экономических специальностей

Иркутск

2003

УДК 51

ББК 22.1

Печатается по решению редакционно-издательского совета

Байкальского государственного университета экономики и права

Рецензент канд. физ.-мат. наук, доц. А. И. Беников

Тарасенко Н.В., Шеломенцева Н.Н.

МАТЕМАТИКА-2. Решение задач оптимизации в Excel: Метод. указ. для студентов экономических специальностей. – Иркутск: Изд-во БГУЭП, 2003. – 43с.

Содержит указания по применению электронных таблиц Microsoft Excel к решению задач оптимизации. Рассматриваются проблемы построения электронных математических моделей линейного программирования и их оптимизации с помощью надстройки «Поиск решения». На конкретных примерах экономического содержания показаны все этапы нахождения оптимального решения и его постоптимального анализа. Приводятся индивидуальные задания для выполнения расчетно-графической работы по данной теме.

Рекомендуется для студентов всех экономических специальностей.

ББК 22.1

Электронная версия:

I:\Study\УМЛ\Кафедра математики\Математика-2\Тарасенко НВ Шеломенцева НН Оптимизация в Excel на сервере БГУЭП.

Регистрационный номер NEL–2003–T59

Введение

При решении задач, возникающих в экономике, часто встает вопрос о выборе наилучшего в некотором смысле варианта решения. При этом на поиск возможного варианта часто влияют разного рода факторы, сужающие рамки выбора. Иначе говоря, требуется решить задачу оптимизации, которая состоит в необходимости выбора наилучшего варианта решений среди некоторого, как правило, ограниченного множества возможных вариантов.

Задача оптимизации может быть сформулирована на языке математики, если множество доступных вариантов удается описать с помощью математических соотношений (равенств, неравенств, уравнений), а каждое решение - оценить количественно с помощью некоторого показателя, называемого критерием оптимальности или целевой функцией. Тогда наилучшим решением будет то, которое доставляет целевой функции наибольшее или наименьшее значение, в зависимости от содержательного смысла задачи. Так, например, при инвестировании ограниченной суммы средств в несколько проектов естественной является задача выбора тех проектов, которые могут принести в будущем наибольшую прибыль. При доставке в магазины продукции от различных поставщиков возникает задача минимизации транспортных затрат.

Процесс формализации задачи называется построением ее математической модели. Он состоит из трех этапов.

1. Выбор параметров задачи, от которых зависит решение. Эти параметры будем называть переменными и обозначать 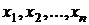, формируя из них вектор .

2. Описание всего множества 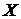допустимых значений переменных – ограничений, связанных с наличием материальных ресурсов, финансовых средств, технологическими возможностями и т.п..

3. Построение числового критерия, по которому можно сравнивать различные варианты решений. Такой критерий принято называть целевой функцией и обозначать через .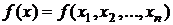

Математическая задача оптимизации состоит в нахождении такого допустимого решения 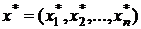, которое доставляет целевой функции наибольшее или наименьшее значение среди всех возможных решений.

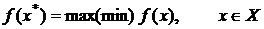Решение называется оптимальным решением задачи оптимизации.

Модели задач оптимизации имеют множество различных постановок. В зависимости от элементов моделей (исходных данных, искомых переменных и типов зависимостей) можно провести следующую их классификацию:

Исходные данные	Искомые переменные	Зависимости	Класс задач
детерминированные	непрерывные	линейные	линейное программирование
детерминированные	целочисленные	линейные	целочисленное программирование
детерминированные	непрерывные, целочисленные	нелинейные	нелинейное программирование
стохастические	непрерывные	линейные, нелинейные	стохастическое программирование

В дальнейшем мы будем рассматривать задачи линейного программирования (ЛП), в которых исходные переменные непрерывны, целевая функция 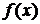линейна, а множество 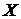описывается линейными равенствами и неравенствами .

Математическая постановка общей задачи ЛП имеет следующий вид.

Найти максимум (или минимум) линейной функции

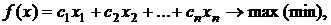
от 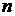переменных 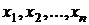, удовлетворяющих линейным ограничениям в форме равенств или неравенств

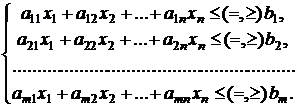
Часто в экономических задачах отдельно выписываются условия неотрицательности переменных, связанные со смыслом экономических показателей, взятых за неизвестные.

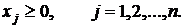
В курсе математика-2 изучаются методы исследования задач линейного программирования, позволяющие найти их решение не прибегая к помощи компьютера. Область применения таких методов как графический, табличный симплекс-метод, ограничивается задачами с небольшим числом переменных и ограничений. В то же время существует мощное, удобное и, что немаловажно, простое средство решения задач оптимизации достаточно большой размерности. Оно поставляется в составе популярного программного пакета Microsoft Excel и называется “ПОИСКРЕШЕНИЯ”.

Подготовка задачи к решению в MS Excel

Подключение надстройки «Поиск решения» в электронной таблице Excel (версии 5-10) осуществляется через меню «Сервис/Надстройки». В выпадающем списке необходимо отметить соответствующий пункт. Если в списке надстроек пункт «Поиск решения» отсутствует, то нужно переустановить пакет Microsoft Office, отметив надстройку «Поиск решения» в разделе «Дополнительные средства Office».

Прежде чем запускать надстройку следует подготовить задачу к решению. Для этого необходимо проделать следующие шаги.

1. Составить на бумаге математическую модель задачи, определив переменные, записав целевую функцию и ограничения (см. введение).

2. Создать табличную (электронную) модель задачи, для чего надо:

a. ввести исходные данные в ячейки таблицы;

b. задать диапазоны ячеек, в которых будут находиться переменные (искомые параметры) задачи. В дальнейшем эти ячейки будем называть изменяемыми ячейками;

c. ввести формулы для вычисления левых частей ограничений и целевой функции задачи ЛП через исходные данные и адреса изменяемых ячеек. Ячейку, содержащую формулу для подсчета целевой функции, будем называть целевой ячейкой.

Только после этого можно решать задачу оптимизации с помощью надстройки «Поиск решения». Заметим, что для решения задач линейного программирования надстройка использует хорошо известный студентам второго курса симплекс-метод, причем в итоге решения выводятся не только оптимальные значения переменных и целевой функции, но и результаты постоптимального анализа.

Рассмотрим подробнее процедуру решения задачи линейного программирования в Excel на конкретном примере.

Дата добавления: 2018-02-15; просмотров: 860; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!