Построение математической модели
Производственная задача. Фирма специализируется на производстве компьютерных столов трех видов А, В, С, что требует различных затрат труда на каждой стадии производства:
| Производственный участок | Затраты труда (чел.-час.) на стол | ||
| А | В | С | |
| Лесопилка | 1 | 2 | 4 |
| Сборочный цех | 2 | 4 | 2 |
| Отделочный цех | 1 | 1 | 2 |
В течение недели можно планировать работу на лесопилке на 360 чел.-час., в сборочном цехе – на 520 чел.-час. и в отделочном цехе – на 220 чел.-час. Цены реализации одного стола типа А, В, С составляют 9, 11, 15 долларов соответственно. Сколько столов каждой модели надо производить в неделю, чтобы максимизировать суммарный недельный доход?
Требуется также провести постоптимальный анализ полученного решения.
Составим математическую модель задачи, выбрав в качестве переменных 
– количество компьютерных столов каждого из трех видов A, B, C, планируемых к выпуску. Тогда ожидаемый суммарный доход может быть подсчитан по формуле
(1)
Переменные задачи удовлетворяют ограничениям
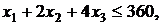
(2)
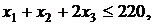
в левых частях которых вычислены затраты трудовых ресурсов на лесопилке, в сборочном и отделочном цехах, а в правых частях записаны максимально возможные запасы этих ресурсов. Учитывая, что переменные задачи по своему экономическому смыслу не могут принимать отрицательные значения, получаем математическую модель задачи оптимального распределения трудовых ресурсов с целью получения максимального дохода от реализации изготовленных компьютерных столов.
|
|
|
.
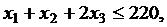
Очевидно, что построенная модель имеет линейную структуру и, следовательно, является задачей линейного программирования.
Создание электронной модели
Чтобы привлечь компьютер к решению этой задачи необходимо ввести исходные данные на лист Excel. Это можно сделать, например, так, как изображено на рис.1. Сначала заносим в таблицу неизменяемые данные: цены продукции, удельные расходы труда на выпуск каждого вида столов и их наличные запасы в каждом цехе.
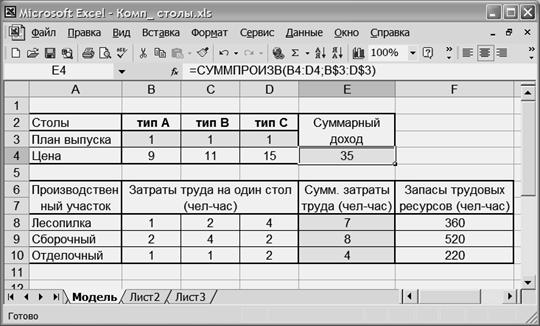
Рис. 1.
Затем заполняем изменяемые ячейки B3:D3, в которых расположены компоненты плана 
. На этапе ввода исходных данных сюда заносятся любые числа, например, единицы. После решения в этих ячейках будут находиться оптимальные значения переменных. Целевая функция (суммарный доход) и левые части ограничений (затраты труда в каждом цехе) подсчитываются в соответствие с составленной моделью по формуле (1) и левым частям (2).
Содержимое соответствующих ячеек приведено ниже
< Е4 > = СУММПРОИЗВ(B4:D4;B$3:D$3) – вычисление суммарного дохода.
|
|
|
< E8 > = СУММПРОИЗВ(B8:D8;B$3:D$3),
< E9 > = СУММПРОИЗВ(B9:D9;B$3:D$3),
< E10 > = СУММПРОИЗВ(B10:D10;B$3:D$3) – вычисление затрат труда в каждом цехе на выпуск всей продукции.
Функция СУММПРОИЗВ(массив1, массив2) относится к разряду математических функций. Она вычисляет произведения соответствующих элементов массивов, после чего суммирует полученные произведения. Вставку функции можно осуществить через одноименный пункт меню Вставка, или с помощью кнопки 
. Если ссылку на диапазон изменяемых ячеек B3:D3 в формуле для < E4 > сделать абсолютной B$3:D$3, для чего можно воспользоваться клавишей F4, то ячейки E8:E10 легко заполнить с помощью операции копирования ячейки E4.
Ячейка Е4, содержащая формулу для вычисления целевой функции является целевой ячейкой.
Дата добавления: 2018-02-15; просмотров: 900; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!