ВЫБОРОЧНЫЕ И СОСТАВНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Приведенные выше обозначения рядов (R5; R10; R20; R40; R80; R160) характеризуют ряды не ограниченные никакими пределами.

В практике конструирования, как правило, применяются ряди с ограниченными пределами. Такие ряды обозначаются: R 20 (160 ... 280) — основной ряд R20, ограниченный членом 160 в качестве нижнего предела и членом 280 в качестве верхнего предела. Пользуясь таблицей 1 запишем в развернутом виде последний ряд чисел:

160-180-200-224-250-280

В стандартизация используют также выборочные ряды. Они применяются в тех случаях, когда ни одна из градаций основных рядов не удовлетворяет поставленным требованиям. Обычно по выборочным рядам строят ряда параметров и размеров являющихся функциями других параметров и размеров, для которых градации приняты по основным рядам. Выборочные ряды образуются из основных или дополнительных путем отбора n-го члена ряда, начиная с любого числа ряда.

Обозначение выборочного ряда состоит из обозначения исходного основного ряда, после которого ставится косая черта и число 2; 3; 4 ... n соответственно.

Если ряд ограничен, обозначение должно содержать члены, ограничивающие ряд; если ряд не ограничен, должен быть указан хотя бы один его член.

Например, R40/5 (... 60) — выборочный ряд, полученный путем отбора каждого пятого члена основного ряда R40 и ограниченный членом 60 в качестве верхнего предела.

Допускается использовать составные ряды, построенные из разных основных и выборочных рядов. Например: 1,0 — I,6 — 2,5 — 4,0 — 6,3 — 8,0 — 10,0. Этот составной ряд составлен из двух рядов: R5 (1,0... ...б,3) и R10 (6,3 … 10,0). Конечные и начальные члены смежных рядов, образующих составной ряд, должны быть одинаковыми. Составные ряды применяются, если требуемая плотность значений параметра в рассматриваемом интервале неодинакова.

ПРИБЛИЖЕННЫЕ ПРЕДПОЧТИТЕЛЬНЫЕ РЯДЫ

Предпочтительные числа, включенные в ГОСТ 8032—84 как уже отмечалось, являются округленными по сравнению с расчетными членами геометрических прогрессий. Однако, как показала практика, в отдельных случаях требуются дополнительные округления стандартизованных чисел. Например, при установлении числа зубьев шестерен нельзя использовать число 31,5 (типичным может быть 32) или нецелесообразно требовать времени экспозиции для фотоаппаратов 1/31,5 с вместо более простого значения 1/30 (число 3,00 отсутствует в рядах R5; R10; R20).

ГОСТ 8032—84 в обоснованных случаях допускает применять вместо основных рядов R ряды R' и R'' приближенных предпочтительных чисел. В ряду R' отдельные предпочтительные числа ряда R заменены величинами первой степени округления, в ряду R'' — второй степени округления.

В альтернативных ситуациях следует отдавать предпочтение числам из ряда R перед числами R', а числам R' перед числами R''. Включение приближенных предпочтительных чисел в дополнительные ряды не допускается.

Перечислим приближенные предпочтительные числа рядов R' и R'', отличающиеся от чисел соответствующего основного ряда.

В ряд R'' 5 входят числа 1,5 и 6,0, соответствующие числам 1,6 и 6,3 ряда R5.

Ряд R'10 идентичен ряду R10, за исключением члена 3,15, который заменен членом 3,20.

Ряд R'' I0 содержит числа: 1,2; 1,5; 3,0; 6,0 (в ряду R''10 они заменяют ближайшие числа ряда R10; далее аналогичные замены).

Вряд R'20 входят числа: 1,1; 2,2; 3,2; 3,6, а в ряд R'' 20 — 1,2; 3,0; 3,5; 5,5; 6,0; 7,0.

В ряд R'40 — 1,05; 1,1; 1,2; 1,3; 2,1; 2,2; 2,4; 2,6; 3,2; 3,4; 3,6; 3,8; 4,2; 4,8.

ПРОИЗВОДНЫЕ И СПЕЦИАЛЬНЫЕ РЯДЫ

Производные и специальные ряды чисел устанавливают в случае, если из—за естественной закономерности изменения значений параметра, не могут быть применены основные, дополнительные, выборочные и составные ряды предпочтительных чисел.

Используют следующие производные предпочтительные ряды: убывающие, комплементарные и арифметические.

Убывающие и комплементарные предпочтительные числа получают на основе убывающей геометрической прогрессии. Убывающие ряды чисел применяются для установления значений параметров, асимптотически приближающихся к нулю, например, загрязнения вещества, Комплементарные ряды чисел следует использовать для установления значений параметров, асимптотически стремящихся к 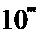(где m. — целое число или нуль), например, чистоты воздуха, КПД, вероятность безотказной работы.

Арифметические предпочтительные ряды чисел получают на основе арифметической прогрессии.

Арифметические ряды необходимо применять при установлении значений параметров:

1) сумма или разность которых долина принадлежать тому же ряду (например, при блочном проектировании и модульной координация размеров);

2) когда равномерная градация обусловлена удобством использования (например, значения аргументов в таблицах, градуирование шкал приборов);

3) когда нужны точные целые значения (например, эталонные значения параметров) и т.д.

Точные значения членов арифметических рядов в интервале 0—1000 представляют собой мантиссы десятичного логарифма исходных (точных) значений предпочтительных чисел рядов R , приведенных в таблице 1.

Обозначения и разности основных и дополнительных арифметических предпочтительных рядов чисел приведены в таблице 2.

Таблица 2 - Взаимосвязь предпочтительных (геометрических) рядов R и арифметических рядов

Обозначение		Значащие цифры разности (точные значения)
исходного геометрического ряда	производного арифметического ряда	Значащие цифры разности (точные значения)
Основные ряды
R5	А20	2
R10	А10	1
R20	А5	5
R40	А2,5	25
Дополнительные ряды
R80	А1,25	125
R160	А0,625	625

Предпочтительные арифметические ряды могут быть положительными и отрицательными или могут переходить через нуль.

В обозначениях арифметических предпочтительных рядов чисел должны указываться их разность и числа, ограничивающие ряд, например:

А 2 (-10 ... + 10)

А 0,5 (0 ... 40)

А 1250 (5 • 10³ ... 2 • 10⁴)

Выборочные арифметические ряды получают по тем же правилам, что и геометрические ряды.

К специальным рядам чисел и значений величины (параметра) относят, например:

1) двоичный ряд, применяемый в вычислительной технике. В этом ряду i-й член ряда находится из выражения:

fi = 2^l (5);

2) форматные ряды стандартных значений линейного размера стороны листа.

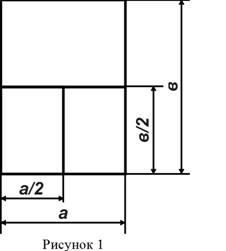
Известно, что есть только одно соотношение сторон прямоугольника, при котором он может быть разделен пополам с сохранением тех же самых пропорций (рисунок 1).

Если а:b = b:2a, то 2a² = b². Извлекая квадратный корень из обеих частей равенства, получим

b = a .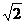

Следовательно, выражение для i-го члена ряда, определяющего размеры сторон листов различного формата будет иметь вид:

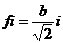(6)

Значение b выбирается из двух условий:

1) выражение для i-го члена равняется 1 м;

2) площадь исходного листа равна 1 м².

Для первого случая b = 1• 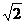= 1414 мм, а для второго случая b = 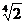= 1189 мм.

Отсюда форматный ряд линейного размера в мм будет в первом случае:

F_a… 1414, 1000, 707, 500, 353, 250, 170, 125, 88 ...

Во втором случае:

F_s ... 1189, 841, 594, 420, 297, 210, 148, 105, 74, 52, 37 ...

На основе членов ряда F_s создана серия форматов листов А, в которой формат А0 является наибольшим. Площадь этого листа - 1 м², а стороны равны соответственно 1189 х 841 мм [8]

Ряд F_a взят за основу серии форматов листов бумаги В. Наибольший размер листа в этой серии имеет размеры 1414 х 1000 мм.

Надо отметить, что серия форматов листов В применяется в исключительных случаях;

3) стандартные ряды номинальной емкости электрических конденсаторов и номинального сопротивления резисторов. Данные ряда построены на база геометрических прогрессий с знаменателями, приведенными в таблице 3:

Таблица 3 – Ряды Е

Обозначение ряда	Е6	Е12	Е24	Е48	Е96
Знаменатель ряда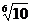

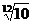
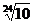
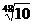
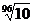
Дата добавления: 2018-02-15; просмотров: 3287; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 Следующая ⇒

Мы поможем в написании ваших работ!