Розрахунок пускових і гальмівних опорів у колі статора асинхронного двигуна
Для зниження пускового струму і струму в режимі гальмування противмиканням у коло статора асинхронних двигунів з короткозамкненим ротором на час пуску, гальмування або реверсу вводять активні або індуктивні опори. Отримані при цьому характеристики розглянуті в лекціях 6 і 7.
Рисунок 5.3 – Трикутник опорів для кола статора асинхронного двигуна
Для розрахунку пускових або гальмівних опорів задаються пусковим струмом або моментом. Якщо потрібно знизити пусковий або гальмівний струм у aі разів, то цей струм у штучній схемі з елементами, які обмежують струм.
Іпуск.ш = aі Іпуск.п, (5.7)
де Іпуск.п — пусковий струм у природній схемі (без опорів).
Пусковий момент на штучній характеристиці, пропорційний квадрату напруги, за рахунок падіння напруги на введених у коло статора опорах буде зменшений у aі2разів (aі <1):
Мпуск.ш = Мпуск.п aі2. (5.8)
Значення зовнішніх активних R1вш та індуктивних X1вш опорів у колі статора звичайно вибирають з умови отримання рівних пускових моментів у природній і штучній схемах. Втрати електричної енергії при пуску або гальмуванні противмиканням з активними опорами будуть більше, ніж при пуску або гальмуванні з індуктивними опорами. Значення моментів на штучній механічній характеристиці з R1вш будуть декілька менше, ніж на відповідній характеристиці з Х1вш.
|
|
|
Щоб отримати задане значення пускового струму або моменту двигуна, його повний опір у режимі короткого замикання (при s = 1) повинен бути
(5.9)
де Zк.ш, Zк — повний опір короткого замикання в штучній і природній схемах увімкнення двигуна; m = Мпуск.ш/ Мпуск.п — коефіцієнт зниження моменту.
Значення опорів, що вводяться в коло статора, отримуються із трикутників опорів, які побудовані для природної та штучної схем у режимі короткого замикання (рис. 5.3). На рис. 5.3, а наведений трикутник опорів при введенні активного опору, а на рис. 5.3, б — індуктивного. Значення активних та індуктивних опорів визначаються зі співвідношень
(5.10)
(5.11)
де Rк і Хк — опори короткого замикання в природній схемі вмикання.
ТЕМА 6 ПЕРЕХІДНІ ПРОЦЕСИ В ЕЛЕКТРОПРИВОДАХ
Лекція 13 Механічні перехідні процеси при лінійних характеристиках двигуна і механізму. Електромеханічна стала часу
При експлуатації електропривода двигун підключають до мережі, змінюють режими його роботи з рухового на гальмівний та навпаки. Перехід електропривода від одного усталеного режиму роботи до іншого називається перехідним режимом.
|
|
|
У перехідному режимі електропривода одночасно і взаємозалежно діють перехідні механічні, електромагнітні та теплові процеси. Механічні та електромагнітні перехідні процеси в сукупності називаються електромеханічним перехідним процесом. При електромеханічному перехідному процесі, який швидко протікає, більш повільний тепловий процес істотно не впливає на зміни параметрів електропривода. Тому надалі буде розглядатися електромеханічний перехідний процес. Перехідний процес обумовлений інерційними масами електропривода та електромагнітною інерцією обмоток електричних машин і пристроїв. Виникає він при пуску в хід, гальмуванні та реверсуванні електропривода, переході двигуна з однієї кутової швидкості на іншу або зміні параметрів у схемі увімкнення, раптовому повному або частковому знятті навантаження.
Мета розрахунку перехідних процесів — визначення часу перехідного процесу і залежностей w = f (t), M = j (t), I = y (t); у деяких випадках — знаходження залежності шляху, який проходить механізм у перехідному режимі, або кута повороту механізму.
|
|
|
Перехідні процеси при лінійних характеристиках. З основного рівняння руху електропривода (1.19) одержимо
де М – Мст = Мдин — позитивний динамічний момент.
Переписуючи рівняння руху відносно dt одержимо
dt = J dw / ( M - Mст) (6.1)
Час, необхідний для зміни кутової швидкості електропривода від початкової wпоч. до кінцевої (усталеної) wу,
(6.2)
З рівняння (6.2) видно, що теоретично t =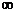 
тому, що при М = Мст величина, яка стоїть під знаком інтеграла, прагне до нескінченності. У практичних розрахунках вважають, що перехідний процес закінчується приблизно при w = (0,95... 0,98) wу.
У найпростішому випадку при М = сопst, Мст = const і J = const час перехідного процесу (с)
t1,2 = J (wу - wпоч)/ M – Mст), (6.3)
де М — момент, який розвивається двигуном при перехідному процесі; у формулі (6.3) вважається постійним протягом усього часу перехідного процесу і приймається рівним середньому моменту Мср.
Час розгону електропривода з нерухомого стану до номінальної швидкості при Мср = const і Мст = const
|
|
|
tр = J wном /(Мср - Мст). (6.4)
Тому що при гальмуванні двигуна Мcт діє узгоджено з Мcp, то час гальмування за тих самих умов від wном до w = 0
tгальм = J wном /(Мср + Мст). (6.5)
Для багатьох робочих машин у процесі роботи Мст = const тому, що в основному він обумовлюється силами тертя (прокатні стани, стрічкові транспортери тощо). У цих машин залежність Mст (w) має вигляд прямої лінії, яка паралельна вісі ординат (див. рис. 1.4, а, б), тобто вважається, що характеристика механізму лінійна.
Для двигуна постійного струму незалежного збудження та асинхронного двигуна з фазним ротором з введеним зовнішнім опором у колі ротора рівняння прямолінійної механічної характеристики [див. (2.19)]
w = w0 - Dw.
Нехай розгін електропривода починається по реостатній характеристиці двигуна (рис. 6.1). Величина Dw може бути знайдена з пропорції, складеної для двох подібних трикутників:
відкіля
Враховуючи те, що Dw = w0 - wу, одержимо
(6.6)
Усталена швидкість
(6.7)
або
wу = w0 (Мк - Мст)/ Мк. (6.7а)
Рівняння (6.7) і (6.7а) також є рівняннями механічної характеристики.
Для розв’язання рівняння руху електропривода
M = Mст + J dw / dt
необхідно знати залежність Мст від w. При Мст = const рівняння (6.7) після диференціювання буде мати вигляд
(6.8)
Підставимо отримане співвідношення (6.8) у рівняння руху електропривода:
(6.9)
Величина J w0 / Мк при Mст = const у цьому рівнянні називається електромеханічною сталою часу Тм, виражається у секундах і характеризує інтенсивність протікання перехідного процесу. Електромеханічною сталою часу називається час, протягом якого електропривод, маючи момент інерції J, розганяється з нерухомого стану до кутової швидкості ідеального холостого ходу w0 під дією незмінного моменту, який дорівнює моменту короткого замикання Мк (або початковому пусковому моменту) двигуна:
Тм = Jw0 / Мк (6.10)
Тому що Мк на реостатних характеристиках визначається активним опором RS якірного або роторного кола, то для двигуна постійного струму незалежного збудження враховуючи (2.7), (2.9) і (2.30)
(6.10а)
а для асинхронного двигуна
(6.10б)
Як видно зі співвідношень (6.10), (6.10 а) і (6.10б), стала часу Тм не залежить від навантаження на валу двигуна і зі збільшенням опору в колі якоря або ротора збільшується (тому що Мк при цьому зменшується).
З рівняння (6.9) після розподілу змінних одержимо
d M /(M - Мст) = - dt / Тм (6.9а)
Проінтегруємо і позначимо постійну інтегрування через ln C. Тоді
ln(M - Mст) = - t/Тм + ln C. (6.11)
Величину С визначимо з початкових умов пуску: t = 0; M = Mк; C = Mк - Mст. Підставимо значення С в рівняння (6.11) і перенесемо ln С в ліву частину:
(6.12)
Після потенціювання
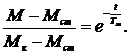(6.13)
Розв'язуючи рівняння відносно М, одержимо закон зміни моменту:
М = Мст (1 – e-t/Тм) + Mк e-t/Тм. (6.14)
Переписуючи рівняння (6.12) відносно t, знайдемо час перехідного процесу:
(6.15)
При лінійних механічних характеристиках двигуна, коли М ≡ І, закон зміни струму аналогічний закону (6.14):
I = Iст (1 – e-t/Тм) + Iк e-t/Тм. (6.16)
У формулах (6.14) і (6.16) Мcт і Iст — момент і струм двигуна в режимі навантаження; t – поточне значення часу від початку перехідного періоду.
Рівняння (6.14) і (6.16) наведені для випадку, коли електропривод розганяється з нерухомого стану при пусковому (або початковому) моменті Mк і струмі Iк. Для цього випадку зміна М та I зображена на рис. 6.2.
У загальному випадку, коли обрані або задані початкові значення Мпоч. і Iпоч, рівняння (6.14) і (6.16) можуть бути представлені у виді
М = Мст + (Mпоч – Мст) e -t/Тм; (6.17)
I = Iст + (Iпоч – Iст) e –t/Тм. (6.18)
Звичайно при пуску та розгоні електропривода застосовують пусковий реостат, ступіні якого виводять послідовно замикаючи (шунтуючи) окремі його секції. При цьому електропривод переходить з однієї (більш м'якої) реостатної характеристики на іншу (більш жорстку) характеристику з меншим опором RS. Початковий пусковий момент М1 (струм I1) двигуна, що обирається за умовами комутації струму або допустимості пускового моменту, на кожній ступіні розгону прагнуть підтримувати незмінним (рис. 6.3).
Момент М2 (струм I2), при якому відбувається шунтування пускових ступіней, приймають декілька більшим, ніж Mст (Iст). Таким чином, на кожній пусковій ступіні момент (струм) підтримують відповідно в межах від М1 до М2 (або від I1 до I2).
Так як момент і кутова швидкість двигуна зв'язані між собою лінійно, то рівняння для зміни кутової швидкості в часі аналогічно (6.17):
w = wу + (wпоч - wу) e-t / Tм. (6.19)
Якщо вважати, що розгін електропривода закінчується при кутовій швидкості (0,95 ... 0,98) wу, то час перехідного процесу до швидкості 0,95 wу складає tр = 3 Tм, а до швидкості 0,98 wу tр= 4 Тм.
Виходячи з рівнянь (6.17) — (6.19) на рис. 6.3 побудовані криві перехідного процесу моменту (струму) і кутової швидкості, які відповідають реостатному пуску в три ступіні. Відповідний час розгону на реостатних характеристиках позначений tр1, tр2, tр3, а час виходу на природну характеристику — tр4. Сумарний час розгону електропривода tр = tр1 + tр2 + tр3 + tр4. Перехідний процес закінчується при М = Мст.
На відміну від процесу пуску та розгону електропривода процес гальмування найчастіше відбувається при одній ступіні реостата в силовому колі двигуна.
Перехідні процеси для моменту, струму і кутової швидкості описуються рівняннями, аналогічними рівнянням (6.17), (6.18)і (6.19), у яких початкові умови — момент, струм і швидкість перед гальмуванням: - Мг, - Іг, wг. Усталеними значеннями при цьому є Мcт, Iст і - wу, які установилися б у випадку активного моменту навантаження (рис. 6.4, а). Електромеханічна стала часу для режиму динамічного гальмування і гальмування противмиканням
Рисунок 6.4 – Механічні характеристики та графіки перехідного процесу при динамічному гальмуванні двигуна
де Мк — момент короткого замикання на гальмовій характеристиці (див. рис. 2.8, 3.13).
Час гальмування tг при відповідних Tм для динамічного гальмування і гальмування противмиканням відповідно
(6.20)
(6.21)
Перехідний процес при гальмуванні до повної зупинки електропривода закінчується при w = 0. Для динамічного гальмування криві зміни М і w до точки A (w = 0) зображені на рис. 6.4, б.
Дата добавления: 2018-02-15; просмотров: 1212; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!