Необходимое и достаточное условие коллинеарности векторов
Векторы. Геометрическое представление вектора. Линейные операции над векторами (сложение (правило треугольников, параллелограмма, многоугольников), вычитание и умножение на действительное число), их свойства.
Вектор − это направленный отрезок. Векторы обозначаются 
или 
, где 
− начало вектора, 
− его конец. Длина вектора называется его модулеми обозначается 
или 
.
Коллинеарные векторы − это векторы, направления которых совпадают или противоположны, что обозначают 
׀׀ 
.
Компланарные векторы − это векторы, лежащие в параллельных плоскостях, в частности, в одной плоскости.
Два вектора 
и 
называются равными, если они имеют одинаковую длину и одинаково направлены. Обозначают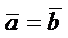 
.
Рассмотрим линейные операции над векторами.
Суммой векторов 
и называется вектор, идущий из начала вектора 
в конец вектора 
при условии, что начало вектора совпадает с концом вектора 
.
Это правило называют правилом треугольника (рис. 2.1, а) или параллелограмма (рис. 2.1, б) сложения векторов.
а) б)
Рис. 2.1 Сложение векторов
по правилу треугольника (а) и параллелограмма (б)
Понятие суммы векторов позволяют ввести:
1) операцию, обратную операции сложения, − разность векторов 
и 
как вектор 
такой, который в сумме с вектором дает вектор (рис. 2.2, а),
2) сложение произвольного конечного числа векторов 
(правило многоугольника) (рис. 2.2, б).
а) б)
Рис.2.2 Вычитание векторов (а) и
сложение векторов по правилу многоугольника (б)
Произведением вектора 
на числоλ называется такой вектор , который удовлетворяет условиям:
а) 
;
б) векторы и − сонаправленные, если число λ > 0, и противоположно направленные, если λ < 0.
Таким образом, из определения операции умножения вектора на число следует, что векторы и 
= λ или сонаправленные или противоположно направленные, т.е. коллинеарные.
Линейная зависимость векторов. Геометрический смысл линейной зависимости двух и трех векторов.
Вектор 
называется линейной комбинацией векторов 
, 
,…, 
, если он получен из этих векторов проведением над ними линейных операций его можно представить в ви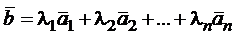де 
, где 
, 
,…, 
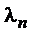− некоторые числа. Это равенство называют также разложением вектора 
по векторам 
, 
,…, 
.
Векторы 
, 
,…, 
являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например, 
. В противном случае (т.е. ни один из векторов 
, 
,…, 
не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
Пара векторов на плоскости является линейно зависимой тогда и только тогда, когда эти векторы коллинеарные.
Тройка векторов в пространстве является линейно зависимой тогда и только тогда, когда эти векторы компланарны.
Необходимое и достаточное условие коллинеарности векторов
Для того что бы 2 не нулевых вектора были колинеларны необходимо и достаточно что бы они были линейно зависимы.
Необходимость:
Достаточность:
Необходимое и достаточное условие компланарности векторов:
Для того что бы 3 не нулевых вектора были компланарными необходимо и достаточно что бы они были линейно зависимы.
Необходимость: дано: 
Очевидно если хотя бы пара из них колинеарны, следовательно они компланарны т.е. линейно зависимы
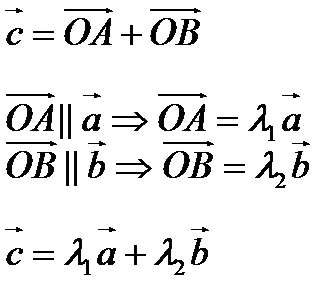
Достаточность:
Дата добавления: 2018-02-18; просмотров: 1949; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!