Формулы деления векторов в данном отношении.
Точка М делит отрезок АВ в отношении λ, если выполняется равенство 
.
Если 
, 
, 
, то
, 
, 
.
Особый интерес представляет случай, когда точка М делит отрезок АВ пополам. Тогда 
=1 и координаты середины отрезка вычисляются по формулам
, 
, 
.
Скалярное произведение векторов.
Скалярным произведением двух векторов 
и 
называется число, равное произведению модулей этих векторов на косинус угла между ними 
.
Свойства скалярного произведения:
1) 
(коммутативность);
2) 
(дистрибутивность);
3) 
, если 
или 
, или 
перпендикулярно 
;
4) 
.
Первые три свойства показывают, что скалярное умножение суммы векторов на другую сумму можно производить по обычному правилу умножения многочленов.
Найдем выражение скалярного произведения векторов 
и 
в декартовых координатах. Для этого запишем разложение векторов и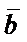 
в базисе 
, 
, 
и с учетом свойства скалярного произведения получим
Учитывая, что
получим
Таким образом,скалярное произведение равно сумме произведений одноименных координат.
Скалярное произведение векторов используется при решении ряда задач:
1) нахождение угла между векторами 
и 
:
;
2) вычисление проекции одного вектора на направление другого вектора:
;
3) проверка перпендикулярности двух векторов:
׀ 
, т.е. 
;
4) вычисление работы постоянной силы 
вдоль прямолинейного участка пути (вектор перемещения 
):
.
Векторное произведение. Геометрический смысл модуля векторного произведения.
|
|
|
Векторным произведение вектора на вектор называется такой вектор 
, который удовлетворяет следующим условиям:
1) модуль вектора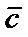 
равен произведению модулей векторов и на синус угла между ними
,
т.е. модуль вектора 
численно равен площади параллелограмма, построенного на векторах и 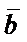как на сторонах;
2) вектор 
перпендикулярен векторам 
и ;
3) вектор 
направлен так, что с конца вектора 
кратчайший поворот от к 
виден происходящим против часовой стрелки.
Свойства векторного произведения:
1) векторное произведение некоммутативно (неперестановочно), при этом 
;
2) для векторного произведения выполняется дистрибутивный (распределительный) закон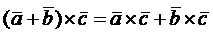 
;
3) 
, где 
− любое действительное число;
4) 
, если векторы и 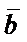коллинеарны или по крайней мере один из сомножителей является нулевым вектором.
Из первых трех свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обычным правилам перемножения многочленов (но порядок следования множителей ввиду некоммутативности векторного произведения меняться не должен).
Найдем векторное произведение векторов 
и в декартовых координатах.
|
|
|
.
Учитывая, что 
,
,
,
получим
.
Векторное произведение используется при решении ряда задач.
Площадь параллелограмма, построенного на векторах 
и равна модулю их векторного произведения 
, а площадь треугольника, построенного на векторах 
и 
, равна 
.
Смешанное произведение векторов. Условие компланарности.
Смешанным произведением трех векторов , и 
называется число, равное векторному произведению векторов и скалярно умноженному на вектор 
: 
. Обозначается 
.
Свойства смешанного произведения:
1) смешанное произведение не изменится, если переставить перемножаемые векторы в круговом порядке
;
2) при перестановке любых двух векторов смешанное произведение изменит только знак
;
3) смешанное произведение компланарных векторов равно 0;
4) модуль смешанного произведения численно равен объему параллелепипеда, построенного на перемножаемых векторах как на сторонах: 
.
Объем треугольной пирамиды, построенной на векторах , 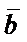и 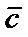определяется по формуле: 
.
Если векторы , и заданы в координатной форме, то их смешанное произведение вычисляется при помощи определителя
.
Дата добавления: 2018-02-18; просмотров: 3170; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!