Поверхности и их уравнения. Плоскость. (...).
В декартовой пространственной системе координат уравнение вида:
Определяет плоск(поверхность) в общем случае.
Линии в пространственной системе координат рассматриваются, как общие точки пересекающихся поверхностей.
Уравнение плоскости проход. через данную точку перп. данному вектору.
Уравнение плоскости проходящей через точку М0 перпендикулярно вектору n.
Уравнение плоскости, проходящие через три заданные точки. Уравнение плоскости в отрезках.
В декартовой системе координат в пространстве каждая плоскость определяется уравнением первой степени (линейным уравнением) и каждое уравнение первой степени определяет плоскость.
Всякий не равный нулю вектор, перпендикулярный данной плоскости, называется нормальным вектором этой плоскости.
Уравнение 
определяет плоскость, проходящуючерез точку 
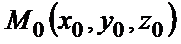, перпендикулярно вектору 
. Если раскрыть скобки в этом уравнении и ввести обозначение 
, то получится общее уравнение плоскости 
. Коэффициенты А, В, С при неизвестных в общем уравнении плоскости − это координаты вектора, перпендикулярного этой плоскости.
Рассмотрим частные случаи расположения плоскостей.
1. Коэффициент 
и уравнение плоскости имеет вид 
. Очевидным решением такого уравнения является нулевое решение ( 
, 
, 
). Значит, это уравнение определяет плоскость, проходящую через начало координат 
.
2. Коэффициент 
и уравнение плоскости имеет вид 
. Так как проекция нормального вектора 
на ось Ох равна 0, то это возможно, если плоскость параллельна оси Ох.
|
|
|
Аналогично, если коэффициент 
и уравнение плоскости имеет вид 
, то эта плоскость параллельна оси Оy. Если уравнение имеет вид 
, т.е. коэффициент при 
равен 0, то это уравнение плоскости, параллельной оси Оz. Вывод: отсутствие в уравнении какой-либо переменной свидетельствует о том, что эта плоскость параллельна оси, соответствующей этой переменной.
3. Коэффициенты 
, 
и уравнение имеет вид 
. Плоскость параллельна осям Ох и Оy и, следовательно, параллельна плоскости Охy.
4. Коэффициенты 
, 
, 
и уравнение имеет вид 
. Плоскость параллельна плоскости Охy (так как 
, 
). Кроме того, она проходит через точку 
(так как 
). Значит уравнение 
(или 
) определяет саму плоскость Охy.
Уравнение плоскости, проходящейчерез три заданные точки 
, 
и 
имеет вид:
.
Составим уравнение плоскости, проходящей через три заданные точки 
, 
и 
:
.
Раскрыв определитель и выполнив преобразования, получим уравнение плоскости в отрезках
.
Здесь a, b, c − отрезки, отсекаемых плоскостью от координатных осей.
Угол между двумя плоскостями, условие параллельности и перпендикулярности плоскостей.
|
|
|
Углом между плоскостями – называется любой из двугранных углов между этими плоскостями.
Угол между плоскостями 
и 
− это угол между их нормальными векторами 
и 
. Поэтому он может быть вычислен с помощью скалярного произведения векторов по формуле
.
Очевидно, если две плоскости параллельны, то их нормальные векторы коллинеарные. Отсюда вытекает условие параллельности плоскостей:
.
Аналогично, условие перпендикулярности плоскостей − это равенство нулю скалярного произведения их нормальных векторов:
.
Дата добавления: 2018-02-18; просмотров: 691; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!