Матричное представление булевых функций
Матричное представление (с использованием кода Грея) булевой функции и сопоставляемых ей допустимых и максимальных интервалов отличается хорошей наглядностью.
Множеству всех наборов значений булевых переменных 
,…, 
(множеству 
всех вершин единичного n-мерного куба) сопоставим прямоугольную матрицу А из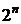 
элементов.
Пусть число столбцов матрицы равно 
, а число ее строк равно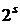 
, где t + s = n.
Каждому набору α значений переменных ,…, сопоставим (взаимнооднозначно) элемент матрицы А. Соответствие зададим специальным образом с помощью надчеркивания строк и столбцов матрицы А, используя код Грея.
Пусть n = 5, t = 3, s = 2. Рассмотрим матрицу А, изображенную на рис.2.3. В ней строкам и столбцам сопоставлены линии разных уровней. Линии одного и того же уровня соответствуют одной и той же переменной и обозначаются именем переменной. Линии разных уровней соответствуют разным переменным.
Будем говорить, что элемент матрицы А представляет набор, в котором переменная 
принимает значение 1, если этот элемент находится под линией, отмеченной переменной , и значение 0 – если рассматриваемый элемент не находится под этой линией. Имея в виду сказанное, сопоставляем элементу, отмеченному точкой на рис. 2.3, набор 11110.
Рис. 2.3
Пусть задано множество 
наборов значений переменных функции f( ,…, ). Сопоставив каждому из них точку на матрице в коде Грея, получим матричное представление булевой функции.
|
|
|
Пусть задан набор значений переменных 11001, найдем соответствующий ему элемент на матрице рис. 2.3. Элемент находится среди столбцов, отмеченных переменными и 
, и принадлежит столбцу, не отмеченному переменной 
. Кроме того, он находится в строках, не отмеченных переменной 
, и принадлежит строке, отмеченной переменной 
.
Матрицы в коде Грея для n < 5 получаются из матрицы рис. 2.3 для n = 5 удалением ее строк и столбцов. Так, для n = 4 матрица может быть получена либо удалением нижней половины строк матрицы рис. 2.3, либо удалением правой половины ее столбцов. Из полученной матрицы можно аналогичным образом построить матрицу для n = 3 и т.д.
Увеличение числа переменных на единицу приводит к увеличению в два раза либо числа столбцов, либо числа строк рассматриваемой матрицы. При этом линии разных уровней исходной матрицы переносятся на новые столбцы (строки) симметрично относительно оси, отделяющей прежнюю матрицу от ее новой добавленной половины. Кроме того, появляется линия дополнительного уровня, охватывающая все добавленные столбцы (строки).
Пусть n = 6, тогда возможны, например, следующие варианты матриц в коде Грея (рис. 2.4):
Рис. 2.4
|
|
|
Итак, можно построить матрицу в коде Грея для любого n. Однако на практике ограничиваются матрицами для n < 10.
КАДР
Матрицы удобны для представления на них интервалов. Выделим простейшие типы интервалов.
Подмножество 
Î называется интервалом ранга r, если оно соответствует элементарной конъюнкции ранга r в том смысле, что на всех элементах этого подмножества и только на них конъюнкция k обращается в единицу.
Отдельный элемент булева пространства размерности n (набор значений n переменных) образует интервал ранга n, представленный точкой в соответствующем элементе матрицы.
Два рядом расположенные элемента матрицы по строке или по столбцу представляют интервал ранга n – 1.
Все элементы некоторой строки матрицы образуют интервал ранга n – t, здесь – число элементов строки матрицы.
Все элементы некоторого столбца матрицы образуют интервал ранга
n – s. Здесь 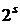– число элементов столбца матрицы.
Четыре рядом расположенные элементы матрицы, образующие квадрат, представляют интервал ранга n – 2.
Такого же ранга интервал образуют четыре элемента, расположенные по углам матрицы.
Каждому интервалу сопоставляется конъюнкция, которая находится по матрице следующим образом. Если все элементы интервала помечены (не помечены) переменной , то переменная включается в конъюнкцию без инверсии (с инверсией).
|
|
|
Имея в виду перечисленные типы интервалов, можно выделять на множестве матрицы в коде Грея более крупные интервалы, в том числе и максимальные. При этом полезно учитывать, что интервал, представленный несколькими областями, образует симметричные структуры на матрице, которые легко выявляются визуально.
Подмножества из , “похожие” на интервал, можно проверить на принадлежность интервалу. Для этого достаточно построить соответствующую подмножеству конъюнкцию и убедиться в совпадении числа элементов подмножества с 
, где r – ранг построенной конъюнкции.
Для получения безызбыточных ДНФ функций небольшого числа переменных, достаточно близких к кратчайшим, можно воспользоваться представлением булевой функции на матрице в коде Грея. При этом не требуется ни построения сокращенной ДНФ, ни построения таблицы Квайна. На рис. 2.5 представлено безызбыточное покрытие максимальными интервалами элементов множества булевой функции. Ему сопоставляется следующая ДНФ: 
Ú 
Ú 
Ú 
Ú 
.
Рис. 2.5
|
|
|
Дата добавления: 2018-02-18; просмотров: 1290; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!