Методы построения сокращенных ДНФ

Метод Квайна–МакКласки

Метод позволяет получить сокращенную ДНФ функции f( ,…, ) из ее совершенной ДНФ и основан на использовании операции поглощения

и операции простого склеивания

= .

ДНФ, сопоставляемая покрытию множества всеми максимальными интервалами, является сокращенной ДНФ функции f. Очевидно, что сокращенная ДНФ единственна для f.

Теорема 2.4 (теорема Квайна). Сокращенная ДНФ булевой функции f( ,…, ) получается из ее совершенной ДНФ путем выполнения всевозможных операций склеивания и поглощения конъюнкций.

Доказательство. Очевидно, поглощаемые конъюнкции не могут присутствовать в сокращенной ДНФ, поскольку не являются простыми импликантами булевой функции f( ,…, ). Покажем, что простые импликанты сокращенной ДНФ могут быть получены из совершенной ДНФ путем многократного выполнения операции простого склеивания.

Выберем некоторую простую импликанту K функции f( ,…, ), представим ее в виде совершенной ДН

Ф, применяя в обратном порядке операцию простого склеивания. Например, K = 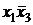, n = 4. Применив операцию простого склеивания по переменной , получим

Ú .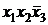

Далее с целью получения совершенной ДНФ применим в обратном порядке операцию простого склеивания к каждой из полученных конъюнкций:

Ú Ú Ú .

Имея совершенную ДНФ конъюнкции K и выполнив простые склеивания обычным образом, получим простую импликанту K. Склеиваем первую и вторую конъюнкции совершенной ДНФ, а затем – третью и четвертую:

Ú .

Выполнив простое склеивание над оставшимися конъюнкциями по переменной , получим простую импликанту K. Принимая во внимание, что все конъюнкции совершенной ДНФ, построенной для простой импликанты K, содержатся среди конъюнкций совершенной ДНФ функции f( ,…, ), приходим к заключению: простая импликанта сокращенной ДНФ получается из совершенной ДНФ путем выполнения, в общем случае многократного, операции склеивания. Ч.Т.Д.

Теорема указывает способ получения сокращенной ДНФ функции f( ,…, ) из ее совершенной ДНФ.

Для изложения, основанного на ней алгоритма, известного как алгоритм Квайна–МакКласки, воспользуемся представлением конъюнкций троичными векторами.

КАДР

2.3.1.1. Представление конъюнкций троичными векторами

Каждой конъюнкции K булевой функции n переменных можно сопоставить n-компонентный троичный вектор следующим образом.

Если в конъюнкции i-я переменная присутствует со знаком инверсии, то i-й компоненте вектора приписывается значение 0, если без инверсии – значение 1. Если i-я переменная в конъюнкции отсутствует, то i-й компоненте сопоставляется значение “–“.

Например, конъюнкции функции 5 переменных сопоставляется вектор 1–01–.

Компоненты со значениями 0, 1 будем называть определенными компонентами троичного вектора, а компоненты со значением “–“ неопределенными.

Между конъюнкциями и троичными векторами имеет место взаимно-однозначное соответствие. Следовательно, операции над конъюнкциями могут быть распространены на операции над троичными векторами. Покажем это для операций поглощения и простого склеивания.

Троичный вектор α поглощает троичный вектор β, если вектор β получается из α заменой некоторых неопределенных компонент α на определенные компоненты. Будем обозначать отношение поглощения между векторами следующим образом: .

Например, α = – –1–0, β = 0–110, .

Для троичных векторов α, β выполняется операция простого склеивания, и результат ее представляется вектором γ, если α, β отличаются друг от друга одной, определенной, например, i-й компонентой. Вектор γ имеет в этой компоненте значение “–“, его остальные компоненты принимают те же значения, что и компоненты векторов α, β.

Пусть α = 01–1–, β = 00–1–, тогда γ = 0– –1–.

Будем считать весом троичного вектора число его единичных компонент. Векторы, веса которых отличаются на единицу, будем называть соседними по весу.

Очевидно, двоичный вектор – это частный случай троичного вектора. Для двоичного вектора множество компонент со значением “–“ пусто.

Перейдем непосредственно к описанию алгоритма Квайна–МакКласки.

КАДР

Алгоритм Квайна–МакКласки

1. Представим совершенную ДНФ булевой функции f( ,…, ) списком двоичных векторов.

2. Упорядочим элементы списка по возрастанию весов векторов. В результате список разобьется на равновесные подмножества векторов.

3. Выполним операции склеивания над векторами соседних по весу подмножеств. Результаты склеиваний занесем в новый список, а векторы, участвующие в склеивании, отметим символом *. В каждом новом списке векторы оказываются разбитыми на равновесные подмножества.

4. Если новый список пуст, переходим к п. 5 алгоритма. Иначе переходим к п. 3 и работаем с новым списком векторов.

5. Выпишем из всех полученных списков, в том числе из исходного упорядоченного списка булевых векторов, векторы, не отмеченный символом *. Образуем из выписанных векторов список, представляющий сокращенную ДНФ булевой функции f( ,…, ).

6. Переходим, если это требуется, к записи сокращенной ДНФ в виде дизъюнкции конъюнкций.

Приведем пример построения сокращенной ДНФ функции по ее совершенной ДНФ:

Ú Ú Ú Ú Ú 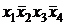Ú Ú .

Представим эту ДНФ списком булевых векторов:

0001
0011
0100
0101
1001
1111
1010
1100

Упорядочим элементы списка по возрастанию весов и разобьем на равновесные подмножества:

1	0001 *
2	0100 *

3	0011 *
4	0101 *
5	1001 *
6	1010
7	1100 *

8	1111

Выполним операции простого склеивания над элементами множеств с весами 1, 2. Получим новый список векторов. В нем слева указаны номера элементов предыдущего списка, участвующих в склеивании. Элементы предыдущего списка, участвующие в склеивании, отмечаются символом *. Новый список представляется в виде

(1,3)	00–1
(1,4)	0–01
(1,5)	–001
(2,4)	010–
(2,7)	–100

Новый список состоит из одного подмножества, следовательно, склеивание его элементов невозможно. Переходим к п. 5 алгоритма. Получаем следующий список троичных векторов:

1010

1111

00–1

0–01

–001

010–

–100

Сокращенная ДНФ имеет вид

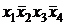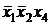Ú Ú Ú Ú Ú Ú .

Отметим, что при реализации алгоритма на этапе склеиваний троичных векторов может потребоваться большой объем вычислений, несмотря на то, что взвешивание троичных векторов позволяет просматривать вместо всевозможных пар векторов – кандидатов на склеивание – только векторы соседних по весу подмножеств.

Для получения минимальных и кратчайших ДНФ из сокращенной, как правило, необходимо выбрасывать некоторые конъюнкции. Ответ на вопрос, какие конъюнкции подлежат исключению, можно получить, построив таблицу Квайна.

КАДР

Таблица Квайна и ее покрытия

Таблица Квайна есть булева матрица, строки которой сопоставлены конъюнкциям сокращенной ДНФ, а столбцы – конъюнкциям совершенной ДНФ. Строки и столбцы могут отмечаться как конъюнкциями, так и представляющими их векторами. Элемент (i, j) матрицы равен 1, если конъюнкция i-й строки поглощает конъюнкцию j-го столбца. Иначе элемент матрицы принимает значение 0. Договоримся нули в матрицу не записывать для удобства ее просмотра. Для нашего примера таблица Квайна представляется в виде

	0001	0011	0100	0101	1001	1111	1010	1100
1010							1		4	A
1111						1			4	B
00–1	1	1							3	C
0–01	1			1					3	D
–001	1				1				3	E
010–			1	1					3	F
–100			1					1	3	G

Рис. 2.2. Таблица Квайна

Здесь конъюнкции, сопоставляемые строкам и столбцам, представлены векторами.

Назовем покрытием столбцов матрицы подмножество ее строк, удовлетворяющее условию: в каждом столбце подмножества содержится хотя бы одна единица.

Заметим, что все множество строк таблицы Квайна является покрытием. В нашем примере можно указать несколько подмножеств строк, являющихся покрытиями. Подмножества будем задавать перечислением номеров строк, образующих покрытие: {1, 2, 3, 4, 5, 7}, {1, 2, 3, 5, 6, 7}.

Имея в виду введенную ранее интерпретацию строк и столбцов, приходим к заключению, что всякому покрытию столбцов таблицы Квайна сопоставляется покрытие множества функции, для которой таблица построена, простыми импликантами этой функции. Среди этих покрытий будем искать такие, которые представляют минимальные и кратчайшие ДНФ функции f. Для этого введем еще ряд определений.

Определение. Покрытие называется безызбыточным, если при удалении из него одной (любой) строки оно перестает быть покрытием множества столбцов таблицы.

Назовем длиной покрытия число его строк.

Определение. Безызбыточное покрытие минимальной длины называется кратчайшим покрытием.

Припишем строкам таблицы Квайна веса, равные рангам сопоставляемых конъюнкций.

Определение. Безызбыточное покрытие с минимальной суммой весов его строк называется минимальным покрытием.

Безызбыточному покрытию сопоставляется безызбыточная, или тупиковая, ДНФ функции f( ,…, ).

Кратчайшему покрытию сопоставляется кратчайшая ДНФ функции f( ,…, ).

Кратчайшей ДНФ функции f( ,…, ) называется ДНФ, реализующая f и содержащая наименьшее число элементарных конъюнкций по сравнению со всеми другими ДНФ, реализующими эту функцию.

Минимальному покрытию сопоставляется минимальная ДНФ функции f( ,…, ).

Минимальной ДНФ функции f( ,…, ) называется ДНФ, реализующая f и содержащая наименьшее число символов переменных по сравнению со всеми другими ДНФ, реализующими эту функцию.

Очевидно, что кратчайшие и минимальные покрытия содержатся среди безызбыточных покрытий.

Итак, задача построения минимальных и кратчайших ДНФ булевой функции f( ,…, ) сводится к построению минимальных и кратчайших покрытий столбцов таблицы Квайна.

В нашем примере приведенные выше покрытия являются одновременно кратчайшими и минимальными. В общем случае минимальное покрытие может не быть кратчайшим.

КАДР

2.3.1.4. Построение всех безызбыточных покрытий

Имея все безызбыточные покрытия, можно выбрать среди них минимальные и кратчайшие покрытия.

Приведем алгоритм построения всех безызбыточных покрытий. С этой целью сопоставим строкам таблицы Квайна заглавные буквы латинского алфавита (рис. 2.2).

Алгоритм

1. Сопоставим каждому столбцу таблицы Квайна элементарную дизъюнкцию, составленную из букв латинского алфавита, отмеченных в столбце единицами.

2. Построим конъюнктивную нормальную форму (КНФ) из полученных элементарных дизъюнкций.

3. Перейдем от КНФ к ДНФ, раскрывая скобки и выполняя операцию поглощения конъюнкций.

Каждая конъюнкция полученной ДНФ сопоставляется некоторому безызбыточному покрытию таблицы Квайна и, следовательно, безызбыточной ДНФ функции f( ,…, ). ДНФ строится из конъюнкций, соответствующих строкам таблицы Квайна, отмеченным буквами в .

Заметим, что для получения минимальных покрытий достаточно приписать конъюнкциям суммы весов строк, отмеченных входящими в конъюнкцию буквами.

Конъюнкции с минимальными суммами представляют всевозможные минимальные ДНФ функции f( ,…, ).

Конъюнкции минимальных рангов представляют всевозможные кратчайшие ДНФ функции f( ,…, ). Проиллюстрируем алгоритм поиска всех безызбыточных покрытий на таблице Квайна рис. 2.2.

Имеем следующую КНФ:

(C Ú D Ú E)(F Ú G) C (D Ú F)E A G B.

Примем во внимание, что для элементарных дизъюнкций, так же как и для элементарных конъюнкций, возможны операции поглощения на основании следующего тождества: (x Ú y) y = y.

Выполнив всевозможные поглощения дизъюнкций, получим более простую КНФ:

C (D Ú F) E A G B.

Далее к ней, применяя п. 3 алгоритма, строим ДНФ:

A B C D E G Ú A B C E F G.

Находим по ее конъюнкциям все безызбыточные ДНФ булевой функции:

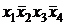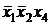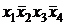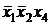= Ú Ú Ú Ú Ú ,

= Ú Ú Ú Ú Ú .

Обе ДНФ являются кратчайшими и минимальными.

Отметим, что алгоритм поиска всех безызбыточных ДНФ булевой функции также связан с большим объемом вычислений. Он, как и алгоритм Квайна, относится к множеству алгоритмов, сложность которых экспоненциально растет с ростом числа переменных функции f( ,…, ).

На практике, имея таблицу Квайна, прибегают к более эффективным в смысле вычислительных затрат алгоритмам, позволяющим найти одно (любое) кратчайшее покрытие, не претендуя на поиск минимального покрытия. Для функций большого числа переменных часто отказываются от построения сокращенной ДНФ, ограничиваясь поиском подмножества простых импликант и поиском безызбыточных покрытий, по возможности близким к кратчайшим.

Важно отметить, что алгоритмы получения покрытий столбцов булевой матрицы ее строками применимы к любым булевым матрицам. При этом строки и столбцы булевой матрицы получают интерпретацию, соответствующую природе решаемой задачи.

Напомним, что поиск хроматического числа в графе сводится к нахождению кратчайшего покрытия столбцов строками булевой матрицы. Строки сопоставляются максимально совместимым подмножествам, а столбцы – вершинам графа.

Сведение той или иной задачи к покрытию столбцов или строк булевой матрицы часто оказывается полезным, с одной стороны, в связи с тем, что уже существуют достаточно быстродействующие алгоритмы, позволяющие находить кратчайшие покрытия для матриц приемлемых размеров, а с другой – для оценки сложности решаемой задачи.

Рассмотрим ситуацию, когда булева функция задана не таблицей, а представлена некоторой ДНФ D = Ú…Ú , существенно более компактной, чем совершенная ДНФ этой функции. Нельзя ли в этом случае обойтись без получения совершенной ДНФ за счет применения в обратном порядке операции простого склеивания, ведь на получение ДНФ D уже могли быть затрачены усилия, связанные с выполнением склеиваний и поглощений конъюнкций? Оказывается, можно. Такую возможность предоставляет метод Блейка.

КАДР

Метод Блейка

Напомним операцию обобщенного склеивания:

Ú = Ú Ú .

Конъюнкцию будем называть результатом обобщенного склеивания. Именно среди результатов обобщенного склеивания, многократно примененного к конъюнкциям произвольной ДНФ булевой функции f( ,…, ), оказываются простые импликанты булевой функции.

Теорема 2.5 (теорема Блейка). Сокращенная ДНФ функции f( ,…, ) получается из произвольной ДНФ этой функции путем выполнения всевозможных операций обобщенного склеивания и поглощения конъюнкций.

Доказательство приведено в работе [Диск.мат. 74].

Изложим на основе теоремы алгоритм Блейка. Пусть предварительно в заданной ДНФ выполнены всевозможные поглощения конъюнкций.

Алгоритм.

1. Начиная со второй конъюнкции в ДНФ D, выбираем очередную конъюнкцию и пытаемся выполнить для нее операцию простого склеивания с предшествующими конъюнкциями D, с первой, второй и т.д. по порядку. Пусть операция склеивания с конъюнкцией , j < i, выполнима и k – результат обобщенного склеивания. Тогда возможны следующие ситуации:

§ k поглощается одной из конъюнкций D, переходим к п. 2 алгоритма,

§ иначе приписываем конъюнкцию k справа к D, исключив из D все конъюнкции, поглощаемые k.

Обозначаем полученную ДНФ также через D и переходим к п. 2 алгоритма.

2. Продолжаем просмотр предшествующих для конъюнкций из D. Если все предшествующие конъюнкции просмотрены, увеличиваем i на единицу, если это возможно, и переходим к п. 1 алгоритма. Если все конъюнкции просмотрены, переходим к п. 3.

3. Очередная ДНФ D представляет сокращенную ДНФ булевой функции f( ,…, ).

Проиллюстрируем применение алгоритма Блейка на примере. Имеем ДНФ: Ú Ú .

Выполнив операцию обобщенного склеивания второй и первой конъюнкций с последующим поглощением конъюнкцией xy первой конъюнкции, получим: Ú Ú .

Выполнив операцию обобщенного склеивания второй и первой конъюнкций, полученной на предыдущем шаге ДНФ, имеем: Ú Ú Ú .

Выполнив операцию обобщенного склеивания третьей и второй конъюнкций с последующим поглощением конъюнкцией y второй, третьей, четвертой конъюнкций, получим сокращенную ДНФ: xz Ú y.

Будем иметь в виду, что если мы хотим получить из построенной методом Блейка сокращенной ДНФ все минимальные или все кратчайшие ДНФ, нам придется извлекать совершенную ДНФ, чтобы воспользоваться таблицей Квайна.

Если ДНФ представляет константу 1, то в процессе реализации всевозможных простых склеиваний эта константа будет получена. Заметим, что применение алгоритма Блейка для проверки ДНФ на представление ею константы 1, как правило, неэффективно в смысле требуемых вычислительных затрат.

КАДР

Дата добавления: 2018-02-18; просмотров: 2571; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!