Получение безызбыточных (тупиковых) ДНФ
Имея сокращенную ДНФ, можно пытаться выбрасывать из нее некоторые конъюнкции, чтобы получать безызбыточные (тупиковые) ДНФ, состоящие, например, из конъюнкций по возможности меньших рангов. Такие безызбыточные ДНФ могут оказаться достаточно близкими к кратчайшим ДНФ, и для их получения не требуется иметь все безызбыточные ДНФ. При этом подходе к получению безызбыточных ДНФ необходимо уметь находить конъюнкции, которые можно исключить из заданной ДНФ, не важно, какой именно: сокращенной или произвольной.
Удаляемая конъюнкция 
должна удовлетворять условию: представляющий ее интервал содержится в объединении интервалов оставшихся конъюнкций заданной ДНФ:
.
Иными словами, конъюнкция поглощается оставшимися конъюнкциями рассматриваемой ДНФ. Речь идет о совместном поглощении конъюнкции .
Можно перейти к следующей постановке задачи. Имеем произвольную конъюнкцию k, не принадлежащую рассматриваемой ДНФ D, необходимо выяснить, не поглощается ли она этой ДНФ. Нас интересует ситуация, когда отдельная конъюнкция ДНФ не поглощает конъюнкцию k.
Определение. Конъюнкции , 
будем называть ортогональными, если сопоставляемые им интервалы имеют пустое пересечение: 
.
В ортогональных конъюнкциях найдется хотя бы одна переменная, такая, что в одной из конъюнкций эта переменная присутствует с инверсией, а в другой – без инверсии.
Например, конъюнкции 
, 
ортогональны по переменной 
.
|
|
|
Очевидно, что конъюнкции ДНФ D, ортогональные конъюнкции k, не могут участвовать в совместном поглощении конъюнкции k, поэтому исключим их все из ДНФ D. Полученную ДНФ обозначим 
. Задачу сведем к проверке поглощения конъюнкции k ДНФ .
Выполним разложение ДНФ по конъюнкции k следующим образом. Каждую конъюнкцию из представим в виде произведения 
, включая в первый сомножитель буквы, присутствующие в k и одновременно. Если таких букв нет, сомножитель равен 1. В включаются остальные буквы конъюнкции .
Итак, = 
.
КАДР
Теорема 2.6. k 
, если и только если 
º 1.
Доказательство. Достаточность. Пусть условие теоремы выполняется. Покажем, что k . Для этого рассмотрим произвольный набор α значений переменных ДНФ. Если k(α) = 0, то значение (α) нас не интересует. Пусть k(α) = 1,тогда по построению = 1 для любого i. Имеем
(α) = 
= 
, но º 1 из условия теоремы. Следовательно, (α) = 1. Поскольку α – произвольный набор, на котором k(α) = 1, k .
Необходимость. Пусть k . Рассмотрим произвольный набор α. Возможны две ситуации:
1. Пусть k(α) = 1, тогда (α) = 1 и (α) = 1. При любом i имеем
1 = (α) = = º 1.
2. Пусть k(α) = 0. Изменим набор α на набор β, так что k(β) = 1, и β отличается от α только по переменным, присутствующим в конъюнкции k, тогда имеем
|
|
|
= 1.
По построению не содержит переменных, общих с конъюнкцией k. Следовательно, º 1. Ч.Т.Д.
Проиллюстрируем применение теоремы примером. Имеем сокращенную ДНФ:
Ú 
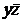Ú xz Ú xy Ú 
Ú 
.
Выделим конъюнкцию и построим для нее ДНФ = Ú xz. Воспользуемся теоремой 2.6, получим из выражение 
Ú x = 1. Следовательно, выделенная конъюнкция поглощается оставшимися конъюнкциями исходной ДНФ и может быть из исходной ДНФ удалена. После удаления конъюнкции имеем ДНФ 
:
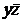= Ú xz Ú xy Ú Ú .
Рассуждая аналогичным образом, получим, что конъюнкция 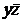может быть удалена из . В результате имеем безызбыточную (тупиковую) ДНФ 
:
= Ú xz Ú xy Ú ,
из которой ни одна из конъюнкций не может быть удалена.
Возьмем, например, конъюнкцию xz. Для нее = xy. Исключив из переменные конъюнкции xz, получим y. Эта функция не равна константе 1, поскольку обращается в единицу на одном из двух наборов представляющей ее таблицы истинности, и т.д.
ДНФ можно рассматривать не только как формулу, но и как множество составляющих ее конъюнкций. Тогда можно говорить о пересечении и объединении ДНФ. Операции объединения и пересечения ДНФ обычно выполняют либо над множествами конъюнкций, представляющих безызбыточные (тупиковые) ДНФ, либо над множествами конъюнкций, представляющих минимальные ДНФ.
|
|
|
Рассмотрим сокращенную ДНФ:
D = 
Ú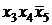 
Ú 
Ú 
Ú 
Ú 
.
Пронумеруем конъюнкции этой ДНФ слева направо. Из нее можно получить две тупиковые ДНФ:
= 
Ú 
Ú 
Ú 
,
= Ú Ú Ú 
.
Образуем пересечение тупиковых ДНФ:
= Ú Ú ,
а затем их объединение:
= Ú Ú Ú Ú .
КАДР
Ядро ДНФ
Определение. Ядром ДНФ D называется совокупность H всех таких конъюнкций:
H = 
,
для каждой из которых выполняется условие
.
Иными словами, конъюнкция входит в ядро H ДНФ D, если она не поглощается совокупностью других конъюнкций ДНФ D.
В рассмотренном выше примере конъюнкции , , входят в ядро, остальные – нет.
Будем иметь в виду, если ДНФ является безызбыточной (тупиковой), то каждая ее конъюнкция входит в ядро.
ДНФ, сопоставляемая безызбыточному покрытию функции f( 
,…, 
), называется безызбыточной или тупиковой.
Теорема 2.7. Конъюнкция k из ДНФ D входит в пересечение тупиковых ДНФ, если и только если она входит в ядро этой ДНФ.
|
|
|
Доказательство. Достаточность. Пусть k входит в ядро. Покажем, что она содержится в пересечении тупиковых ДНФ. Допустим противное, то есть k не содержится в пересечении тупиковых ДНФ. Это значит, что она была исключена при построении одной из тупиковых ДНФ. Однако тогда 
Í 
, то есть не принадлежит ядру ДНФ. Пришли к противоречию.
Необходимость. Пусть k входит в пересечение тупиковых ДНФ. Покажем, что она принадлежит ядру ДНФ. Допустим противное: k не принадлежит ядру. Тогда для нее выполняется условие Í , то есть k может быть удалена при построении некоторой тупиковой ДНФ. Значит, k не принадлежит пересечению тупиковых ДНФ. Пришли к противоречию. Ч.Т.Д.
КАДР
Будем иметь в виду, что для некоторых функций совершенная ДНФ совпадает с сокращенной и, следовательно, совершенная ДНФ является минимальной и кратчайшей одновременно. Речь идет о совершенной ДНФ, конъюнкции которой попарно ортогональны по двум и более переменным. Такие ДНФ встречаются на практике, представляя, например, кодовые слова равновесных кодов, кодов Бергера и т.д.
Сокращенная ДНФ монотонной функции совпадает со своим ядром и, значит, является минимальной и кратчайшей ДНФ одновременно. Это утверждается в нижеследующей теореме.
Функция 
называется монотонной, если для любых двух наборов a и b таких, что 
, имеет место неравенство f (a) £ f (b).
Теорема 2.8. Сокращенная ДНФ монотонной функции не содержит отрицаний переменных и является ее единственной минимальной (кратчайшей) ДНФ.
Доказательство. Докажем сначала первую часть утверждения. Рассмотрим простую импликанту k функции f( ,…, ) ранга r и представим ее в виде 
. Простая импликанта, так же как и функция, обращается в единицу на всяком наборе α значений переменных ,…, , удовлетворяющем условию: 
= … = 
= 1,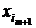 
= … = 
= 0. В силу монотонности функция f( ,…, ) обращается в единицу на всяком наборе a, удовлетворяющем условию = … = = 1. Последнее означает, что конъюнкция 
является импликантой функции f( ,…, ). Тогда конъюнкция k не является простой импликантой этой функции. Пришли к противоречию, следовательно, допущение о наличии отрицаний переменных в простых импликантах сокращенной ДНФ монотонной функции f( ,…, ) не верно.
Итак, на основании только что доказанного произвольная простая импликанта k ранга r монотонной функции f( ,…, ) представляется в виде 
. Покажем, что она не может быть исключена из сокращенной ДНФ функции. Рассмотрим набор α значений переменных ,…, такой, что в нем = … = = 1, 
= … = 
= 0. Покажем, что на этом наборе только конъюнкция k обращается в единицу. Допустим, что найдется другая простая импликанта 
, которая обращается в единицу на этом наборе. По доказанному ранее не содержит отрицаний переменных. Следовательно, поглощает k, то есть k не является простой импликантой. Пришли к противоречию. Делаем заключение: k является единственной простой импликантой, обращающейся в единицу на наборе α, значит, k нельзя исключить из сокращенной ДНФ. В силу произвольного выбора k ни одну из простых импликант нельзя исключить из сокращенной ДНФ функции f( ,…, ). Значит, сокращенная ДНФ является минимальной (кратчайшей) ДНФ монотонной функции. Ч.Т.Д.
КАДР
Дата добавления: 2018-02-18; просмотров: 1141; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!