Для розв’язування яких математичних задач застосовується симплекс метод?

⇐ ПредыдущаяСтр 5 из 15Следующая ⇒

Симплекс-метод — це ітераційна обчислювальна процедура, яка дає змогу, починаючи з певного опорного плану, за скінченну кількість кроків отримати оптимальний план задачі лінійного програмування. Він був розроблений 1949 року американським вченим Дж. Данцігом.

Симплекс-метод застосовується для вирішення задач математичного програмування. Також до задач, які вирішуються симплексним методом можна віднести такі типові економічні задачі, як «Визначення найкращого складу суміші», «Задача про оптимальний план випуску продукції», «Задача про вибір оптимальної програми», «Транспортна задача», «Задача про розміщення» та інші.

Як вибрати спрямовуючий вектор-стовпець?

Після заповнення табл. розраховують значення оцінок плану (останній рядок): . Потім згідно з умовою оптимальності плану задачі лінійного програмування, якщо всі (для задачі на максимум), то план є оптимальним. Допустимо, що одна з оцінок , тоді план не є оптимальним і необхідно здійснити перехід до наступного опорного плану, якому буде відповідати більше значення функціонала. Якщо від’ємних оцінок кілька, то включенню до базису підлягає вектор, який вибирається як 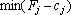. Мінімум знаходять для тих індексів j, де . Якщо існує кілька однакових значень оцінок, що відповідають 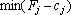, то з відповідних їм векторів до базису включають той, якому відповідає максимальне значення функціонала.

Якщо хоча б для однієї від’ємної оцінки всі коефіцієнти розкладу відповідного вектора недодатні, то це означає, що функціонал є необмеженим на багатограннику розв’язків, тобто багатогранник у даному разі являє собою необмежену область і розв’язком задачі є .

Нехай , тобто мінімальне значення досягається для k-го вектора . Тоді до базису включається вектор . Відповідний стовпчик симплексної таблиці називають напрямним.

22. Що означає "виродження" опорного плану? Як його позбутися?

Опорний план транспортної задачі, як зазначалося раніше, має містити не більше ніж (m + n – 1) відмінних від нуля компонент. Якщо їх кількість дорівнює (m + n – 1), то такий опорний план називають невиродженим. Якщо ж кількість додатних компонент менша ніж (m + n – 1), то опорний план є виродженим. Вироджений план може виникати не лише за побудови опорного плану, але і при його перетвореннях у процесі знаходження оптимального плану. Найчастіше, щоб позбутися виродженості опорного плану, в деякі клітини таблиці транспортної задачі в необхідній кількості вводять нульові постачання. Обсяги запасів постачальників і потреби споживачів після цього не змінюються, однак клітини зі значенням «нуль» вважаються заповненими. Головною умовою при введенні нульової поставки є збереження необхідної і достатньої умови опорності плану транспортної задачі — його ациклічності. Клітина має вибиратись у такий спосіб, щоб неможливо було побудувати замкнений цикл.

23. Поясніть геометричну інтерпретацію задачі лінійного програмування

Кожна нерівність цієї системи геометрично визначає півплощину з граничною прямою a_i₁x₁ + a_i₂x₂ = b_i (i = 1, 2, ...,т). Умови невід’ємності змінних визначають півплощини з граничними прямими х₁ = 0 та х₂ = 0. Система сумісна, тому півплощини як опуклі множини, перетинаючись, утворюють спільну частину, що є опуклою множиною і являє собою сукупність точок, координати кожної з яких є розв’язком даної системи. Сукупність цих точок (розв’язків) називають багатокутником розв’язків, або областю допустимих планів (розв’язків) задачі лінйного програмування. Це може бути точка (єдиний розв’язок), відрізок, промінь, багатокутник, необмежена багатокутна область. Якщо система обмежень сумісна, то за аналогією з тривимірним простором вона утворює спільну частину в n-вимірному просторі — опуклий багатогранник допустимих розв’язків. Отже, геометрично задача лінійного програмування являє собою відшукання координат такої точки багатогранника розв’язків, при підстановці яких у цільову лінійну функцію остання набирає максимального (мінімального) значення, причому допустимими розв’язками є усі точки багатогранника розв’язків. Цільову функцію (Z) в п-вимірному просторі основних змінних можна геометрично інтерпретувати як сім’ю паралельних гіперплощин, положення кожної з яких визначається значенням параметра Z. Властивість 1. (Теорема 1) Множина всіх планів задачі лінійного програмування опукла. Властивість 2. (Теорема 2) Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин многогранника розв’язків. Якщо цільова функція набуває екстремального значення більш як в одній вершині цього многогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин. Властивість 3. (Теорема 3) Якщо відомо, що система векторів А1, А2,…, Аk (k≤n) у розкладі А1х1+А2х2+…+Аnxn=А0, де всі х_j≥0, то точка Х=(х1, х2,…, х_k, 0,…, 0) є кутовою точкою багатогранника розв’язків. Властивість 4. (Теорема 4) Якщо Х=(х1, х2,…, х_n) – кутова точка багатогранника розв’язків, то вектори в розкладі А1х1+А2х2+…+Аnxn=А0, Х≥0, що відповідають додатним х_j, лінійно незалежні.

24. Скільки змінних та обмежень має двоїста задача відповідно до прямої?

Двоїста задача має дві змінні, а отже, її можна розв’язати графічно (рис. 3.2).

Рис. 3.2

Найбільшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:

Отже, Y* = (– 2/3; 4/3); mах F = 1 х (– 2/3) + 4 х 4/3 = 14/3.

Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості. Підставимо Y* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:

Оскільки перше обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то висновуємо, що перша змінна прямої задачі дорівнюватиме нулю х1 = 0 (перша частина другої теореми двоїстості). Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки друга компонента плану у2 = 4/3 додатна, то друге обмеження прямої задачі для Х*виконуватиметься як строге рівняння (друга частина другої теореми двоїстості). Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х1 = 0, та визначити решту змінних: тобто Х* = (0; 5/3; 2/3), min Z = 1 х 0 + 2 х 5/3 + 2 х 2/3 = 14/3. Умова min Z = max F = 14/3 виконується, і тому Х* = (0; 5/3; 2/3); Y* = (– 2/3; 4/3) є оптимальними планами відповідно прямої та двоїстої задач.

Дата добавления: 2018-02-18; просмотров: 1278; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!