Економічна інтерпретація прямої та двоїстої задач лінійного програмування
Чи забезпечуэ принцип оптимальності незалежність наступних розв’зків від здобутих раніше?
Ні не забезпечує
Принцип оптимальності
З викладених у попередніх параграфах міркувань можна висновувати, що для прийняття оптимального рішення на k-му кроці багатокрокового процесу потрібна оптимальність рішень на всіх його попередніх кроках, а сукупність усіх рішень дає оптимальний розв’язок задачі лише в тому разі, коли на кожному кроці приймається оптимальне рішення, що залежить від параметра етапу 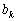 , визначеного на попередньому кроці.
, визначеного на попередньому кроці.
Цей факт є основою методу динамічного програмування і є сутністю так званого принципу оптимальності Р. Белмана, який формулюється так:
Оптимальний розв’язок багатокрокової задачі  має ту властивість, що яким би не був стан системи
має ту властивість, що яким би не був стан системи  в результаті деякої кількості кроків, необхідно вибирати управління
в результаті деякої кількості кроків, необхідно вибирати управління  на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.
на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.
Доведемо справедливість такого твердження, міркуючи від супротивного. Нехай маємо задачу на максимізацію функції  і вектор
і вектор  є її оптимальним планом (стратегією, поведінкою) n-крокового процесу (n-вимірної задачі) з початковим параметром стану b.
є її оптимальним планом (стратегією, поведінкою) n-крокового процесу (n-вимірної задачі) з початковим параметром стану b.
Принцип оптимальності еквівалентний твердженню, що вектор  повинен бути оптимальним планом
повинен бути оптимальним планом  -крокового процесу
-крокового процесу  -вимірної задачі з початковим параметром стану
-вимірної задачі з початковим параметром стану 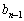 , що дорівнює
, що дорівнює  . Припустимо протилежне, тобто що вектор
. Припустимо протилежне, тобто що вектор  не є оптимальним планом відповідного процесу, а ним є якийсь інший план
не є оптимальним планом відповідного процесу, а ним є якийсь інший план  . Тоді дістанемо:
. Тоді дістанемо:
|
|
|
 ,
,
але
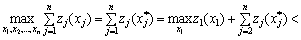
 ,
,
що суперечливо. Отже, принцип оптимальності доведено.
2. Охарактеризуйте головні групи методів розв’язування задач цілочислового програмування.
Для знаходження оптимальних планів задач цілочислового програмування застосовують такі групи методів:
1) точні методи:
o методи відтинання;
o комбінаторні методи;
2) наближені методи.
Основою методів відтинання є ідея поступового «звуження» області допустимих розв’язків розглядуваної задачі. Пошук цілочислового оптимуму починається з розв’язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисловості змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисловість змінних, багатогранник допустимих розв’язків послабленої задачі поступово зменшують доти, доки змінні оптимального розв’язку не набудуть цілочислових значень.
До цієї групи належать:
а) методи розв’язування повністю цілочислових задач (дробовий алгоритм Гоморі);
|
|
|
б) методи розв’язування частково цілочислових задач (другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).
Комбінаторні методи цілочислової оптимізації базуються на ідеї перебору всіх допустимих цілочислових розв’язків, однак, згідно з їх процедурою здійснюється цілеспрямований перебір лише досить невеликої частини розв’язків.
Найпоширенішим у цій групі методів є метод гілок і меж.
Починаючи з розв’язування послабленої задачі, він передбачає поділ початкової задачі на дві підзадачі через виключення областей, що не мають цілочислових розв’язків, і дослідження кожної окремої частини багатогранника допустимих розв’язків.
Для розв’язування задач із бульовими змінними застосовують комбінаторні методи, причому, оскільки змінні є бульовими, то методи пошуку оптимуму значно спрощуються.
Досить поширеними є також наближені методи розв’язування цілочислових задач лінійного програмування. Оскільки для практичних задач великої розмірності за допомогою точних методів не завжди можна знайти строго оптимальний розв’язок за прийнятний час або для розв’язування задачі використовуються наближено визначені, неточні початкові дані, то часто в реальних задачах досить обмежитися наближеним розв’язком, пошук якого є спрощеним.
|
|
|
Значна частина наближених алгоритмів базується на використанні обчислювальних схем відомих точних методів, таких, наприклад, як метод гілок і меж.
До наближених методів належать: метод локальної оптимізації (метод вектора спаду); модифікації точних методів; методи випадкового пошуку та ін.
Головними показниками для зіставлення ефективності застосування конкретних наближених алгоритмів на практиці є такі: абсолютна  та відносна
та відносна 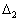 похибки отриманих наближених розв’язків.
похибки отриманих наближених розв’язків.
 ,
,  ,
,
де F — цільова функція (в даному разі для визначеності допускаємо вимогу відшукання максимального її значення); Х1— наближений розв’язок, знайдений деяким наближеним методом; Х* — оптимальний план задачі.
3. Дайте геометричну інтерпретація прямої та двоїстої задачі лінійного програмування
Економічна інтерпретація прямої та двоїстої задач лінійного програмування
Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею.
Економічну інтерпретацію кожної з пари таких задач розглянемо на прикладі виробничої задачі (§ 2.1).
Пряма задача: max F = c1x1 + c2x2 + … + cnxn (3.1)
за умов:  (3.2)
(3.2)
|
|
|
 . (3.3)
. (3.3)
Необхідно визначити, яку кількість продукції кожного j-го виду 
 необхідно виготовляти в процесі виробництва, щоб максимізувати загальну виручку від реалізації продукції підприємства. Причому відомі: наявні обсяги ресурсів —
необхідно виготовляти в процесі виробництва, щоб максимізувати загальну виручку від реалізації продукції підприємства. Причому відомі: наявні обсяги ресурсів —  ; норми витрат і-го виду ресурсу на виробництво одиниці j-го виду продукції —
; норми витрат і-го виду ресурсу на виробництво одиниці j-го виду продукції —  , а також
, а також  — ціни реалізації одиниці j-ої продукції.
— ціни реалізації одиниці j-ої продукції.
Розглянемо тепер цю саму задачу з іншого погляду. Допустимо, що за певних умов доцільно продавати деяку частину чи всі наявні ресурси. Необхідно визначити ціни ресурсів. Кожному ресурсу 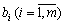 поставимо у відповідність його оцінку
поставимо у відповідність його оцінку  . Умовно вважатимемо, що
. Умовно вважатимемо, що  — ціна одиниці і-го ресурсу.
— ціна одиниці і-го ресурсу.
На виготовлення одиниці j-го виду продукції витрачається згідно з моделлю (3.1)—(3.3) m видів ресурсів у кількості відповідно  . Оскільки ціна одиниці і-го виду ресурсу дорівнює
. Оскільки ціна одиниці і-го виду ресурсу дорівнює  , то загальна вартість ресурсів, що витрачаються на виробництво одиниці j-го виду продукції, обчислюється у такий спосіб:
, то загальна вартість ресурсів, що витрачаються на виробництво одиниці j-го виду продукції, обчислюється у такий спосіб:
 .
.
Продавати ресурси доцільно лише за умови, що виручка, отримана від продажу ресурсів, перевищує суму, яку можна було б отримати від реалізації продукції, виготовленої з тих самих обсягів ресурсів, тобто:
 .
.
Зрозуміло, що покупці ресурсів прагнуть здійснити операцію якнайдешевше, отже, необхідно визначити мінімальні ціни одиниць кожного виду ресурсів, за яких їх продаж є доцільнішим, ніж виготовлення продукції. Загальну вартість ресурсів можна виразити формулою:
 .
.
Отже, в результаті маємо двоїсту задачу:
 (3.4)
(3.4)
за умов:  (3.5)
(3.5)
 (3.6)
(3.6)
Тобто необхідно визначити, які мінімальні ціни можна встановити для одиниці кожного і-го виду ресурсу 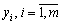 , щоб продаж ресурсів був доцільнішим, ніж виробництво продукції.
, щоб продаж ресурсів був доцільнішим, ніж виробництво продукції.
Зауважимо, що справжній зміст величин 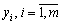 — умовні ціни, що виражають рівень «цінності» відповідного ресурсу для даного виробництва. Англійський термін «shadow prices» у літературі перекладають як «оцінка» або «тіньова, неявна ціна». Академік Л. В. Канторович назвав їх об’єктивно обумовленими оцінками відповідного ресурсу.
— умовні ціни, що виражають рівень «цінності» відповідного ресурсу для даного виробництва. Англійський термін «shadow prices» у літературі перекладають як «оцінка» або «тіньова, неявна ціна». Академік Л. В. Канторович назвав їх об’єктивно обумовленими оцінками відповідного ресурсу.
Задача (3.4)—(3.6) є двоїстою або спряженою до задачі (3.1)—(3.3), яку називають прямою (основною, початковою). Поняття двоїстості є взаємним. По суті мова йде про одну і ту ж задачу, але з різних поглядів. Дійсно, не важко переконатися, що двоїста задача до (3.4)—(3.6) збігається з початковою. Тому кожну з них можна вважати прямою, а іншу — двоїстою. Симетричність двох таких задач очевидна. Як у прямій, так і у двоїстій задачі використовують один набір початкових даних: 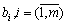 ,
,  ;
;  . Крім того, вектор обмежень початкової задачі стає вектором коефіцієнтів цільової функції двоїстої задачі і навпаки, а рядки матриці А (матриці коефіцієнтів при змінних з обмежень прямої задачі) стають стовпцями матриці коефіцієнтів при змінних в обмеженнях двоїстої задачі. Кожному обмеженню початкової задачі відповідає змінна двоїстої і навпаки.
. Крім того, вектор обмежень початкової задачі стає вектором коефіцієнтів цільової функції двоїстої задачі і навпаки, а рядки матриці А (матриці коефіцієнтів при змінних з обмежень прямої задачі) стають стовпцями матриці коефіцієнтів при змінних в обмеженнях двоїстої задачі. Кожному обмеженню початкової задачі відповідає змінна двоїстої і навпаки.
Початкова постановка задачі та математична модель може мати вигляд як (3.1)—(3.3), так і (3.4)—(3.6). Отже, як правило, кажуть про пару спряжених задач лінійного програмування.
4. Сформулюйте принцип оптимальності Р.Белмана.
Принцип оптимальності
З викладених у попередніх параграфах міркувань можна висновувати, що для прийняття оптимального рішення на k-му кроці багатокрокового процесу потрібна оптимальність рішень на всіх його попередніх кроках, а сукупність усіх рішень дає оптимальний розв’язок задачі лише в тому разі, коли на кожному кроці приймається оптимальне рішення, що залежить від параметра етапу 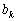 , визначеного на попередньому кроці.
, визначеного на попередньому кроці.
Цей факт є основою методу динамічного програмування і є сутністю так званого принципу оптимальності Р. Белмана, який формулюється так:
Оптимальний розв’язок багатокрокової задачі  має ту властивість, що яким би не був стан системи
має ту властивість, що яким би не був стан системи  в результаті деякої кількості кроків, необхідно вибирати управління
в результаті деякої кількості кроків, необхідно вибирати управління  на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.
на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.
Доведемо справедливість такого твердження, міркуючи від супротивного. Нехай маємо задачу на максимізацію функції  і вектор
і вектор  є її оптимальним планом (стратегією, поведінкою) n-крокового процесу (n-вимірної задачі) з початковим параметром стану b.
є її оптимальним планом (стратегією, поведінкою) n-крокового процесу (n-вимірної задачі) з початковим параметром стану b.
Принцип оптимальності еквівалентний твердженню, що вектор  повинен бути оптимальним планом
повинен бути оптимальним планом  -крокового процесу
-крокового процесу  -вимірної задачі з початковим параметром стану
-вимірної задачі з початковим параметром стану 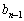 , що дорівнює
, що дорівнює  . Припустимо протилежне, тобто що вектор
. Припустимо протилежне, тобто що вектор  не є оптимальним планом відповідного процесу, а ним є якийсь інший план
не є оптимальним планом відповідного процесу, а ним є якийсь інший план  . Тоді дістанемо:
. Тоді дістанемо:
 ,
,
але
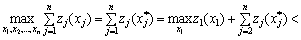
 ,
,
що суперечливо. Отже, принцип оптимальності доведено.
5. Як визначити, що виробництво продукції є нерентабельним (рентабельним)?
Оцінку рентабельності продукції, що виготовляється на підприємстві, можна здійснювати за допомогою двоїстих оцінок та обмежень двоїстої задачі, які характеризують кожний вид продукції. Ліва частина кожного обмеження двоїстої задачі є вартістю відповідних ресурсів, які використовують для виробництва одиниці j-ї продукції. Якщо ця величина перевищує ціну одиниці продукції (сj), то виготовляти таку продукцію невигідно, вона нерентабельна і в оптимальному плані прямої задачі відповідна їй змінна хj = 0. Якщо ж загальна оцінка всіх ресурсів дорівнює ціні одиниці продукції, то виготовляти таку продукцію доцільно, вона рентабельна і в оптимальному плані прямої задачі відповідна змінна хj > 0. Підставимо значення оптимального плану двоїстої задачі Y* у її систему обмежень. Якщо вартість ресурсів на виробництво одиниці продукції (ліва частина обмеження) перевищує ціну цієї продукції (права частина обмеження), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
6. Що означає "правильне відтинання"?
Алгоритм, запропонований Гоморі, передбачає застосування досить простого способу побудови правильного відтинання.
Нехай маємо задачу цілочислового програмування:
 (6.5)
(6.5)
за умов:  ,
,  (6.6)
(6.6)
 ,
,  (6.7)
(6.7)
 — цілі числа
— цілі числа  . (6.8)
. (6.8)
Допустимо, що параметри  — цілі числа. Не враховуючи умови цілочисловості, знаходимо розв’язок задачі (6.5)—(6.7) симплексним методом. Нехай розв’язок існує і міститься в симплексній таблиці. Розглянемо довільний оптимальний план
— цілі числа. Не враховуючи умови цілочисловості, знаходимо розв’язок задачі (6.5)—(6.7) симплексним методом. Нехай розв’язок існує і міститься в симплексній таблиці. Розглянемо довільний оптимальний план  задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну
задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну  через вільні змінні:
через вільні змінні:  . (6.9) Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення:
. (6.9) Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення: 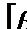 — ціла частина числа b,
— ціла частина числа b, 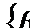 — дробова частина числа b. Отримаємо:
— дробова частина числа b. Отримаємо:  , (6.10)
, (6.10)
або
 . (6.11) Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (6.5)—(6.7). Допустимо тепер, що розглянутий план
. (6.11) Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (6.5)—(6.7). Допустимо тепер, що розглянутий план  є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (6.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:
є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (6.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:
 , (6.12) де N — деяке ціле число. Величина N не може бути від’ємною. Якщо б
, (6.12) де N — деяке ціле число. Величина N не може бути від’ємною. Якщо б  , то з рівняння (6.12) приходимо до нерівності:
, то з рівняння (6.12) приходимо до нерівності:
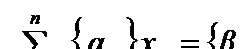 . Звідки
. Звідки  . Тобто це означало б, що дробова частина
. Тобто це означало б, що дробова частина 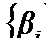 перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним. Якщо від лівої частини рівняння (6.12) відняти деяке невід’ємне число, то приходимо до нерівності:
перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним. Якщо від лівої частини рівняння (6.12) відняти деяке невід’ємне число, то приходимо до нерівності:  ,(6.13) яка виконується за допущенням для будь-якого цілочислового плану задачі (6.5)—(6.7). У такий спосіб виявилося, що нерівність (6.13) є шуканим правильним відтинанням.
,(6.13) яка виконується за допущенням для будь-якого цілочислового плану задачі (6.5)—(6.7). У такий спосіб виявилося, що нерівність (6.13) є шуканим правильним відтинанням.
7. Як розрахувати інтервали можливих змін цін на одиницю кожного виду продукцї?
Під впливом різних обставин ціна одиниці продукції на підприємстві може змінюватися. І тому завжди цікаво знати, у межах яких змін ціни продукції кожного виду оптимальний план її виробництва залишається таким: Х * = (0; 0; 35; 45). Для визначення інтервалів зміни коефіцієнтів цільової функції скористаємось тим, що при цьому симплекс-таблиця, яка відповідає оптимальному плану, зберігає свій вигляд за винятком елементів оцінкового рядка. Нові оцінки (Zj – Cj) мають задовольняти умову оптимальності задачі максимізації, тобто бути невід’ємними. Зміну коефіцієнта С1 позначимо DС1. Оскільки х1 — небазисна змінна, то в симплекс-таблиці зміниться лише відповідна оцінка Z1 – C1: (Z1 – C1) = 4 ? (–2) + 0 ? 1 +3 ? 3/2 – (2 + DС1) = 5 – DС1. За умови Z1 – C1 ? 0 дістанемо нерівність 5 – DС1 ? 0, тобто DС1 ? 5. Це означає, що коли ціна одиниці продукції А за інших однакових умов зросте не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться Х * = (0; 0; 35; 45). Лише максимальний дохід зміниться на max ?Z= DС1х1. Аналогічно розраховується інтервал зміни коефіцієнта DС2: (Z2 – C2) = 5/2 – DС2 ? 0; DС2 ? 5/2. Зі зростанням ціни одиниці продукції В на 5/2 ум. од. за інших однакових умов оптимальний план виробництва продукції не зміниться, а max ?Z = DС2Х2.
Поясніть, що називається областю доступних планів..
Вектор Х = (х1, х2, …, хп), координати якого задовольняють системі обмежень називають допустимим розв’язком, або допустимим планом задачі. Сукупність допустимих розв’язків (планів) задачі утворює область допустимих розв’язків задачі.
Опорним планом задачі лінійного програмування називається план, утворений координатами вершини многогранника планів задачі.
Якщо задача лінійного програмування має розв’язок і серед її планів є опорні, то хоча б один із них буде оптимальним.
Сукупність усіх розв’язків задачі лінійного програмування є многогранною опуклою множиною, яку називають многогранником розв’язків.
Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин многогранника розв’язків. Якщо цільова функція набуває екстремального значення більш як в одній вершині цього многогранника, то вона досягає його і в будь-який точці, що є лінійною комбінацією таких вершин.
9. Яка задача математичного програмування називається цілочисловою
Існує доволі широкий клас задач математичного програмування, в економіко – математичних моделях яких одна або кілька змінних мають набувати цілих значень, наприклад, коли йдеться про кількість верстатів у цеху, тобто коли така вимога випливає з особливостей технології виробництва. До цілочислового програмування належать також задачі оптимізації, в яких змінні набувають лише двох значень – 0 або 1 (бульові, або бінарні, змінні). До цілочислового програмування відносять задачі про призначення, найкоротший шлях і т. ін. У реальних задачах часто цілочислових значень набувають не всі, а одна чи кілька змінних. Такі задачі називають частково цілочисловими. Особливість геометричної інтерпретації цілочислової задачі в порівнянні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисловості розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок.
10. Опишіть алгоритм методу Гоморі
Алгоритм, запропонований Гоморі, передбачає застосування досить простого способу побудови правильного відтинання.
Нехай маємо задачу цілочислового програмування:
 (6.5)
(6.5)
за умов:  ,
,  (6.6)
(6.6)
 ,
,  (6.7)
(6.7)
 — цілі числа
— цілі числа  . (6.8)
. (6.8)
Допустимо, що параметри  — цілі числа. Не враховуючи умови цілочисловості, знаходимо розв’язок задачі (6.5)—(6.7) симплексним методом. Нехай розв’язок існує і міститься в симплексній таблиці. Розглянемо довільний оптимальний план
— цілі числа. Не враховуючи умови цілочисловості, знаходимо розв’язок задачі (6.5)—(6.7) симплексним методом. Нехай розв’язок існує і міститься в симплексній таблиці. Розглянемо довільний оптимальний план  задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну
задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну  через вільні змінні:
через вільні змінні:  . (6.9) Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення:
. (6.9) Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення: 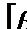 — ціла частина числа b,
— ціла частина числа b, 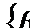 — дробова частина числа b. Отримаємо:
— дробова частина числа b. Отримаємо:  , (6.10)
, (6.10)
або
 . (6.11) Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (6.5)—(6.7). Допустимо тепер, що розглянутий план
. (6.11) Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (6.5)—(6.7). Допустимо тепер, що розглянутий план  є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (6.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:
є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (6.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:
 , (6.12) де N — деяке ціле число. Величина N не може бути від’ємною. Якщо б
, (6.12) де N — деяке ціле число. Величина N не може бути від’ємною. Якщо б  , то з рівняння (6.12) приходимо до нерівності:
, то з рівняння (6.12) приходимо до нерівності:
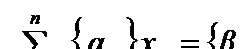 . Звідки
. Звідки  . Тобто це означало б, що дробова частина
. Тобто це означало б, що дробова частина 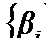 перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним. Якщо від лівої частини рівняння (6.12) відняти деяке невід’ємне число, то приходимо до нерівності:
перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним. Якщо від лівої частини рівняння (6.12) відняти деяке невід’ємне число, то приходимо до нерівності:  ,(6.13) яка виконується за допущенням для будь-якого цілочислового плану задачі (6.5)—(6.7). У такий спосіб виявилося, що нерівність (6.13) є шуканим правильним відтинанням.
,(6.13) яка виконується за допущенням для будь-якого цілочислового плану задачі (6.5)—(6.7). У такий спосіб виявилося, що нерівність (6.13) є шуканим правильним відтинанням.
Дата добавления: 2018-02-18; просмотров: 1353; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
