Термодинамическое определение
Термодинамическое определение внутренней энергии указывает на способ измерения этой величины. В математическом выражении для первого начала термодинамики:
где
· 
— подведённое к телу количество теплоты, измеренное в джоулях
· 
— работа, совершаемая телом против внешних сил, измеренная в джоулях
необходимо положить 
для адиабатически изолированной системы. Приняв какое-либо состояние системы за нулевое, можно измерить работу, совершаемую внешними силами при переходе из нулевого состояния в любое другое состояние (или обратно). Тем самым система будет «энергетически проградуирована», каждому её состоянию будет сопоставлено определенное значение внутренней энергии[2]. Такая система, в свою очередь, сможет служить прибором (калориметром), с помощью которого можно будет измерять изменение внутренней энергии других систем, приводимых в тепловой контакт с системой.
Для квазистатических процессов выполняется следующее соотношение:
где
· 
— температура, измеренная в кельвинах
· 
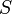— энтропия, измеренная в джоулях/кельвин
· 
— давление, измеренное в паскалях
· 
— химический потенциал
· 
— количество частиц в системе
48) Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.
Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие сопытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.
|
|
|
Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия 
становится функцией не только температуры, но и объёма.
Уравнение Ван-дер-Ваальса — это одно из широко известных приближённых уравнений состояния, имеющее компактную форму и учитывающее основные характеристики газа с межмолекулярным взаимодействием[1].
Уравнение состояния
Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.
Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где
· — давление,
· 
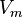— молярный объём,
· 
— абсолютная температура,
· 
— универсальная газовая постоянная.
Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка 
учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка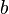 
— объем молекул газа.
|
|
|
Для 
молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
где
· 
— объём,
19) Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль.
Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
20)
) 
волчок.
5. Тензор момента инерции
Рассмотрим твердое тело, закрепленное в точке О. Пусть г = — радиус-вектор точки М этого тела, v — скорость точки М.
Как известно, момент импульса N определяется соотношением , где V — объем тела, dm = ρ dV (ρ — плотность тела).
Обозначая через Ni контравариантные координаты вектора N и используя формулу (8.60) для векторного произведения, получим
(напомним, что сikl = gis cskl, где cskl — координаты дискриминантного тензора в данном базисе пространства Е3, см. п. 6 §3 этой главы).
|
|
|
По теореме Эйлера существует мгновенная ось вращения тела. Обозначая через ω вектор мгновенной угловой скорости, получим v = [ωr]. Снова обращаясь к формуле (8.60) для векторного произведения, найдем
vl = clpn ωp rn. (8.82)
Подставляя найденное выражение vl в правую часть (8.81) и учитывая независимость ωр от переменных интегрирования, получим следующее выражение для Ni:
Кинетическая энергия волчка dEkп = ωkdLk,
11. Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F :
Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
где a— угол между r и F; r sina = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.
Моментом силы относительно неподвижной оси z называется скалярная величина Mz , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента Мz не зависит от выбора положения точки О на оси z.
|
|
|
Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью: 
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: 
где r — радиус-вектор, проведенный из точки О в точку A, p=mv — импульс материальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р.
Модуль вектора момента импульса
где a — угол между векторами r и р, l — плечо вектора р относительно точки О.
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.
Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
Используя формулу (17.1) v = wr, получим 
т. е. 
Закон сохранения момента импульса: момент импульса замкнутой
системы сохраняется, т.е. не изменяется с течением времени: 
12. Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы . Тело при этом, как правило, рассматривается как материальная точка, а центр также считается точечным, обычно совпадая с физическим источником силы; в простейшем случае он фиксирован в пространстве.
Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды.
5. Инерциа́льная система отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся. Инерциальными называют системы отсчета, в которых выполняется закон инерции. Закон же инерции заключается в том, что тела сохраняют свою скорость неизменной, если на них не действуют другие тела.
1 закон Ньютона. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы(или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
2 закон Ньютона. В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.F=ma
3 закон Ньютона. Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
6. Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени. (в поступательном движении).Во вращательном движении момент силы, действуя в течение определённого времени, создаёт импульс момента силы. Импульс момента силы — это мера воздействия момента силы относительно данной оси за данный промежуток времени.
Работа силы и ее выражение через криволинейный интеграл При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:
Здесь точкой обозначено скалярное произведение, 
— вектор перемещения; подразумевается, что действующая сила 
постоянна в течение всего того времени, за которое вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений 
если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат, интеграл определяется следующим образом:
,
где 
и 
— радиус-векторы начального и конечного положения тела соответственно.
55. Первое начало термодинамики. Вечный двигатель первого рода.
Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.
Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца[1]. Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.
Вечный двигатель первого рода — устройство, способное бесконечно совершать работу без затрат топлива или других энергетических ресурсов. Согласно закону сохранения энергии, все попытки создать такой двигатель обречены на провал. Невозможность осуществления вечного двигателя первого рода постулируется в термодинамике как первое начало термодинамики.
История: Попытки исследования места, времени и причины возникновения идеи вечного двигателя — задача весьма сложная. Не менее затруднительно назвать и первого автора подобного замысла. К самым ранним сведениям о Perpetuum mobile относится, по-видимому, упоминание, которое мы находим у индийского поэта, математика и астронома Бхаскары, а также отдельные заметки в арабских рукописях XVI в., хранящихся в Лейдене, Готе и Оксфорде[1]. В настоящее время прародиной первых вечных двигателей по праву считается Индия. Так, Бхаскара в своём стихотворении, датируемом примерно 1150 г., описывает некое колесо с прикреплёнными наискось по ободу длинными, узкими сосудами, наполовину заполненными ртутью. Принцип действия этого первого механического перпетуум мобиле был основан на различии моментов сил тяжести, создаваемых жидкостью, перемещавшейся в сосудах, помещённых на окружности колеса. Бхаскара обосновывает вращение колеса весьма просто: «Наполненное таким образом жидкостью колесо, будучи насажено на ось, лежащую на двух неподвижных опорах, непрерывно вращается само по себе». Первые проекты вечного двигателя в Европе относятся к эпохе развития механики, приблизительно к XIII веку. К XVI—XVII векам идея вечного двигателя получила особенно широкое распространение. В это время быстро росло количество проектов вечных двигателей, подаваемых на рассмотрение в патентные ведомства европейских стран. Среди рисунков Леонардо Да Винчи была найдена гравюра с чертежом вечного двигателя.
56. Внутренняя энергия реального газа.
В отличие от идеальных газов, где внутренняя энергия представляет собой лишь кинетическую энергию движения молекул, зависящую от температуры и не зависящую от занимаемого газом объема, поскольку в газе отсутствует межмолекулярное взаимодействие, в реальных газах межмолекулярные взаимодействия играют существенную роль. Поэтому внутренняя энергия реального газа определяется суммой потенциальной энергии взаимодействия молекул и кинетической энергии их движения.
Так как потенциальная энергия взаимодействия молекул зависит от их взаимного расположения, то она должна изменяться при изменении объема газа. Потенциальную энергию взаимодействия молекул 1 моль газа можно вычислить по формуле добавочное внутреннее давление, входящее в уравнение Ван-дер-Ваальса.
Подставив значение рм в уравнение (2.109), имеем
Эта энергия имеет отрицательный знак, так как молекулярные силы, создающие внутреннее давление, являются силами притяжения.
Используя закон Джоуля, можно вычислить внутреннюю энергию реального газа:
По формуле (2.110) определяется внутренняя энергия 1 моль реального газа, внутренняя энергия v моль определяется по формуле
Внутренняя энергия реального газа зависит как от температуры, так от объема.
43.БАРОМЕТРИЧЕСКАЯ ФОРМУЛА И РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
Барометрическая формула.
Если температура не зависит от высоты, то давление газа меняется с высотой по закону:
,Где
h- высота
R=8.31Дж/(моль*К) – молярная газовая постоянная
k=1,38*10-23 Дж/К – постоянная Больцмана
M- молярная масса; m- масса одной молекулы; T-температура
Поделив барометрическую формулу на kT, с учетом уравнения состояния идеального газа, получим распределение Больцмана — зависимость концентрации молекул от потенциальной энергии:
где — Eп потенциальная энергия молекулы. В однородном поле силы тяжести Eп=mgh .
44. Закон Максвелла о распределении по скоростям и энергиям.
Для вывода функции распределения молекул по скоростям f(v) равной отношению числа молекул dN, скорости которых лежат в интервале от v до v + dv к общему числу молекул N и величине интервала dv
Используя методы теории вероятностей, Максвелл нашел функцию f (v) - закон распределения молекул идеального газа по скоростям:
f (v) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т)
f(v) зависит от отношения кинетической энергии молекулы, отвечающей рассматриваемой скорости к величине kT характеризующей среднюю тепловую энергию молекул газа.
Скорости, характеризующие состояние газа:
7. Консервативные и неконсервативные силы
Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное.
Характерное свойство таких сил – работа на замкнутой траектории равна нулю:
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.
Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное.
Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
8. Потенциальная энергия.
Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил.
Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.
ЕП1 - ЕП2 = -DЕП = А12конс, 
.
Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.
.
Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.
Её связь с силой
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы 
, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии 
. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.
Для установления этой связи вычислим элементарную работу 
, совершаемую силами поля при малом перемещении 
тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой 
. Эта работа равна
где 
- проекция силы на направление .
Поскольку в данном случае работа совершается за счет запаса потенциальной энергии , она равна убыли потенциальной энергии 
на отрезке оси :
Из двух последних выражений получаем
Откуда
Последнее выражение дает среднее значение на отрезке . Чтобы
получить значение в точке нужно произвести предельный переход:
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
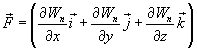
в математике вектор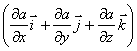 
,
где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом 
.Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком
| (4.15) |
Вопрос 23
)Преобразования Лоренца сохраняют инвариантным интервал для любой пары событий (точек пространства-времени) — то есть любой пары точек пространства-времени Минковского:
В 1892 году Лоренц ввёл теорию сокращения, предполагающую сокращение длин всех твёрдых тел в направлении движения, количественно совпадающее с тем, что понимается сейчас под лоренцевым сокращением.
Преобразования Лоренца были впервые опубликованы Лоренцем в 1904 году, но в то время их форма была несовершенна. К современному, полностью самосогласованному виду их привели французский математик А. Пуанкаре и параллельно и независимо А. Эйнштейн в 1905 году.
впоследствии формально-аксиоматической трактовке этих преобразований.
Лоренц-инвариантность — свойство физических законов записываться одинаково во всех инерциальных системах отсчета (с учетом преобразований Лоренца). Принято считать, что этим свойством должны обладать все физические законы, и экспериментальных отклонений от него не обнаружено. Однако некоторые теории пока не удаётся построить так, чтобы выполнялась лоренц-инвариантность.
Инвариант
Понятие инвариантности (инвариантов) в физике лежит в русле принятого в математике понятия «инвариант преобразований (группы преобразований)» (той или иной конкретной группы преобразований — сдвигов времени, преобразований Лоренца и т. п.).
Инвариант в физике — физическая величина, значение которой в некотором физическом процессе не изменяется с течением времени. Примеры: энергия, компоненты импульса и момента импульса в замкнутых системах.
Вопрос 24.
два события, одновременные в одной системе отсчёта, могут оказаться не одновременными в другой системе отсчёта.пояснение
Предположим, что рядом с каждыми часами в обеих системах отсчёта находятся наблюдатели. Положив в преобразованиях Лоренца 
, получаем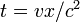 
. Это означает, что наблюдатели в системе 
, одновременно с совпадением времени на центральных часах, регистрируют различные показания на часах в системе 
. Для наблюдателей, расположенных справа от точки 
, с координатами 
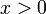, в момент времени часы неподвижной системы отсчёта показывают «будущее» время: 
. Наблюдатели , находящиеся слева от , наоборот, фиксируют «прошлое» время часов
Дата добавления: 2018-02-18; просмотров: 948; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!