Механические модели. Число степеней свободы.

Механика есть наука о механическом движении тела. Механика делится на три раздела: кинематику, динамику и статику.

Кинематика - раздел механики, в котором дается математическое описание движения тел, но не объясняется причины, определяющие тот или иной характер их движения.

Динамика – изучает механические движения, в зависимости от вызывающих его причин

Статика – изучает равновесие твердых тел.

Основными понятиями классической механики, составляющими механическую модель мира, являются абсолютное пространство, абсолютное время и материальная точка.

Абсолютное пространство можно представить себе как пространство внутри ящика, стенки которого раздвинуты до бесконечности. Оно вмещает в себя всю материю, но от нее не зависит . Абсолютное пространство одновременно неосязаемо и незыблемо. Основными его свойствами являются однородность и изотропность, т.е. все точки абсолютного пространства и все направления в нем равноценны.

Абсолютное время t по определению протекает равномерно, не зависит от свойств материи и от места в пространстве , т.е. предполагается, что существует принципиальная возможность измерить величину t посредством синхронизированных часов сразу во всех точках пространства, и в результате этих измерений получить всюду одно и то же значение t.

Материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь.

Абсолютно твердым телом называется система материальных точек, расстояние между которыми со временем не изменяются. Следовательно, размеры и форма абсолютно твердого тела сохраняются с течением времени.

Тело, относительно которого положение и рассматривают перемещение относительно других тел, называется телом отсчета. Для количественного описания движения других тел с этим телом связывают некоторую систему координат. Приборы для измерения времени t и координат x, y ,z произвольной точки пространства вместе с телом, на котором они находятся, составляют систему отсчета.

Число независимых координат, полностью определяющее положение тела в пространстве называют числом степеней свободы.

Линия, описанная материальной точкой, называется ее траекторией.

Длина траектории, описанная материальной точкой, называется длиной пути.

Кинематика материальной точки. Тангенциальное и нормальное ускорения. Радиус кривизны траектории.

Движение материальной точки считается известным , если заданы функции x=x(t), y=y(t), z=z(t), при помощи которых в любой момент времени t определить ее положение в пространстве.

Совокупность функций эквивалента зависимости радиус-вектора тела от времени:

Линия, которую прочерчивает материальная точка при своем движении в пространстве , называется ее траекторией

Вектор 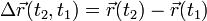называется вектором перемещения частицы из точки P₁ в точку P₂, а вектор - ее средней скоростью за время от t₁ и t₂

Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:

Характеризует быстроту перемещения материальной точки.

Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:

Характеризует быстроту изменения скорости.

Вектор ускорения частицы можно представить в виде суммы двух взаимно ортогональных вектора и

Величина называется тангенциальным ускорением и характеризует величину изменения модуля скорости:

Величина называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:

. ,где R – радиус кривизны траектории.

Если траекторией движения частицы является окружность, то центр кривизны есть центр окружности, а радиус кривизны равен ее радиусу. В силу теоремы Пифагора модули векторов a, и связаны соотношением a²= ²+ ²

Дата добавления: 2018-02-18; просмотров: 813; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!