Применение одношаговых методов для решения обыкновенных
Дифференциальных уравнений высоких порядков
Преобразуем дифференциальное уравнение (7.1) n-го порядка к системе n дифференциальных уравнений 1-го порядка

| (7.16) |
Запись уравнения (7.1) в виде системы (7.16) называется формой Коши. Начальные условия (7.1') при таком преобразовании выглядят так:
| z1(x0)=z1,0 ; z2(x0)=z2,0 ; z3(x0)=z3,0 ; . . . ; zn(x0)=zn,0 ; | (7.16’) |
Для примера преобразуем к форме Коши уравнение Бесселя :
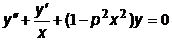 .
.
Обозначим искомую функцию y(x) через z1(x), а ее первую производную - z2(x). Тогда получим систему уравнений первого порядка, эквивалентную исходному уравнению:

Вычислительный алгоритм "усовершенствованного" метода Эйлера для задачи Коши (7.16,7.16') выглядит аналогично (7.8):

| (7.17) |
где i=1,2,...,n ;  ; k=1,2,...,n .
; k=1,2,...,n .
Вычислительный алгоритм "модифицированного" метода Эйлера для задачи Коши (7.16,7.16') выглядит аналогично (7.12):

| (7.18) |
где i=1,2,...,n ; 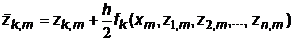 ; k=1,2,...,n .
; k=1,2,...,n .
Вычислительная схема метода Рунге-Кутта четвертого порядка для задачи Коши (7.16,7.16') имеет вид:
 , ,
| (7.19) |
| где | K i,0 = h fi(xm, z 1,m, z 2,m,..., z n,m), |
| K i,1 = h fi(xm+0.5h, z 1,m+0.5K1,0, z 2,m+0.5K2,0,..., z n,m+0.5Kn,0), | |
| K i,2 = h fi(xm+0.5h, z 1,m+0.5K1,1, z 2,m+0.5K2,1,..., z n,m+0.5Kn,1), | |
| K i,3 = h fi(xm+h, z 1,m+K1,2, z 2,m+K2,2,..., z n,m+Kn,2); | |
| i=1,2,...,n. |
Аналогичным образом обобщается на случай системы уравнений и схема (7.14) Кутта-Мерсона.
Общая характеристика одношаговых методов
Всем одношаговым методам присущи определенные общие черты:
1) Чтобы получить информацию в новой точке, надо иметь данные лишь в одной предыдущей точке. Это свойство можно назвать "самостартованием", поэтому одношаговые методы в литературе иногда называются самостартующими.
2) В основе всех одношаговых методов лежит разложение функции в ряд Тейлора, в котором сохраняются члены, содержащие h в степени до k включительно. Целое число k называется порядком метода. Погрешность на шаге имеет порядок k+1.
3) Все одношаговые методы не требуют действительного вычисления производных - вычисляется лишь сама функция, однако могут понадобиться ее значения в нескольких промежуточных точках. Это влечет за собой дополнительные затраты времени и усилий.
4) Свойство "самостартования" позволяет легко менять величину шага интегрирования h.
Методы прогноза и коррекции
Эти методы в отличие от рассмотренных выше являются многоступенчатыми. Алгоритмы таких методов основываются на аппроксимации интерполяционными полиномами либо правой части обыкновенного дифференциального уравнения f(x,y), либо интегральной кривой y=y(x). Ниже рассматриваются два таких метода: метод Адамса и метод Гира.
Метод Адамса
Суть метода Адамса состоит в следующем: одним из одношаговых методов, например, методом Рунге-Кутта четвертого порядка строится искомая интегральная кривая y=y(x) в нескольких точках x1,x2,...,xn, а затем к ним применяются методы аппроксимации для получения решений в новых точках, лежащих как внутри промежутка [x1,xn] - (интерполяция), так и за его пределами (экстраполяция).
Рассмотрим четырехточечный вариант метода Адамса для задачи Коши (7.2),(7.2').
С помощью любого из одношаговых методов вычислим решения y1,y2,y3 заданного уравнения в точках x1,x2,x3. Правая часть (7.2) - функция f(x,y) на интегральной кривой, соответствующей начальному условию (x0,y0), будет, очевидно, функцией только одного аргумента x: f(x,y) = f(x, y(x)) = f(x), значения которой в рассматриваемых точках обозначим f0, f1, f2, f3 (f0 - значение f(x,y) в точке (x0,y0), заданной начальными условиями (7.2’)). В окрестности узлов x0,x1,x2,x3 функцию f(x) приближенно заменим интерполяционным полиномом Ньютона
| f(x)= f0+ f01(x-x0)+f012(x-x0)(x-x1)+f0123(x-x0)(x-x1)(x-x2), | (7.20) |
где f01, f012, f0123 - разделенные разности.
Представим искомое решение y4 в точке x4=x3+h в виде тейлоровского разложения около точки x3:
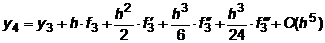 , ,
| (7.21) |
где 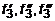 - производные по x от правой части исходного уравнения в точке x3.
- производные по x от правой части исходного уравнения в точке x3.
Дифференцируя полином (7.20) получим выражения для производных:
 (x)= (x)=
| f01+f012(x-x0+x-x1)+f0123[(x-x0)(x-x1)+(x-x0)(x-x2)+ (x-x1) (x-x2)]= = f01+f012(2x-x0-x1)+f0123[3x2-2x(x0+x1+x2)+ x0x1+x0x2+x1x2]; |
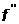 (x)= (x)=
| 2f012+2f0123(3x-x0-x1-x2); |
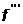 (x)= (x)=
| 6f0123. |
Эти соотношения при x=x3 в случае равноотстоящих узлов принимяют вид:
 =(2f0+9f1-18f2+119f3) / h ; =(2f0+9f1-18f2+119f3) / h ;
| |
 =(-f0+4f1-5f2+2f3) / h2 ; =(-f0+4f1-5f2+2f3) / h2 ;
| (7.22) |
 =(-f0+3f1-3f2+f3) / h3 . =(-f0+3f1-3f2+f3) / h3 .
|
Подставляя производные (7.22) в разложение (7.21) получим экстраполяционную формулу Адамса:
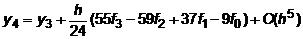
| (7.23) |
имеющую четвертый порядок точности.
Изменяя количество членов, учитываемых в разложении (7.21), можно получить формулы Адамса различных порядков.
Остаточный член формулы (7.23) равен
 .
.
Значительная величина коэффициента (  ) в этом остаточном члене обусловлена тем, что точка x4 лежит вне интервала расположения узлов, по которым построен полином Ньютона. Т.е. здесь мы имеем дело с экстраполяцией, погрешность которой всегда больше, чем погрешность интерполяции. С целью уменьшения погрешности можно получить аналогичным способом, но для узлов x1,x2,x3,x4 интерполяционную формулу Адамса :
) в этом остаточном члене обусловлена тем, что точка x4 лежит вне интервала расположения узлов, по которым построен полином Ньютона. Т.е. здесь мы имеем дело с экстраполяцией, погрешность которой всегда больше, чем погрешность интерполяции. С целью уменьшения погрешности можно получить аналогичным способом, но для узлов x1,x2,x3,x4 интерполяционную формулу Адамса :

| (7.24) |
Эта формула является неявной, т.к. искомая величина y4 необходима для вычисления значения функции f4=f(x4,y4) правой части дифференциального уравнения. Выражение (7.24) можно рассматривать как нелинейное уравнение относительно неизвестной y4 и решать его одним из методов решения трансцендентных уравнений. Обычно здесь используется метод простых итераций, т.к. уравнение (7.24) уже имеет необходимую для этого метода форму  . При этом в качестве начального приближения берется значение y4, определенное по экстраполяционной формуле (7.23).
. При этом в качестве начального приближения берется значение y4, определенное по экстраполяционной формуле (7.23).
Формулу (7.23) называют формулой прогноза, а формулу (7.24) - формулой коррекции.
Эти две формулы без труда переносятся на дифференциальные уравнения высоких порядков, записанные в форме Коши.
Метод Гира
Одним из одношаговых методов получим решения y1,y2,y3 задачи Коши (7.2,7.2’) в точках x1,x2,x3. В окрестности узлов x0,x1,x2,x3,x4 искомое решение y(x) приближенно заменим интерполяционным полиномом Ньютона четвертой степени:
| y(x)= + | y0+y01(x-x0)+y012(x-x0)(x-x1)+ y0123(x-x0)(x-x1)(x-x2)+y01234(x-x0)(x-x1)(x-x2)(x-x3), | (7.25) |
где y01, y012, y0123, y01234 - разделенные разности порядков с первого по четвертый.
Левую часть уравнения (7.2), т.е. производную y’(x), приближенно найдем путем дифференцирования по x полинома (7.25):
| y’(x)= + - | y01+y012(2x-x0-x1)+y0123[3x2-2x(x0+x1+x2)+ x0x1+x0x2+x1x2]+ y01234[4x3-3x2(x0+x1+x2)+2x(x0x1+x0x2+x0x3+x1x2+x1x3+x2x3)- x0x1x2-x0x1x3-x0x2x3-x1x2x3]; | (7.26) |
Разделенные разности для равноотстоящих узлов выражаются через узловые значения аппроксимируемой функции:
| y01 | =(y1-y0) / h, | |
| y012 | =(y2-2y1+y0) / (2h2), | (7.27) |
| y0123 | =(y3-3y2+3y1- y0) / (6h3), | |
| y01234 | =(y4-4y3+6y2-4y1+y0) / (24h4). |
Полагая в (7.26) x=x4 и учитывая (7.27), получим:
| y’(x4)=(3y0-16y1+36y2-48y3+25y4) / (12h). | (7.28) |
C другой стороны, исходное дифференциальное уравнение (7.2) при x=x4 принимает вид:
| y’(x4)=f(x4,y4). | (7.29) |
Приравнивая правые части (7.28) и (7.29), находим:
| y4=[3(4hf(x4,y4)-y0)+16y1-36y2+48y3] / 25. | (7.30) |
Формула (7.30) представляет собой неявную схему Гира четвертого порядка для решения задачи Коши (7.2,7.2’). Выражение (7.30) есть уравнение относительно y4, для решения которого можно применить метод простых итераций. Начальное приближение к y4 можно получить из следующих соображений. Полагая в выражении (7.26) x=x3, имеем:
| y’(x3)=(-y0+6y1-18y2+10y3-y4) / (12h). | (7.31) |
Приравнивая правые части (7.2) при x=x3 и выражения (7.31), получим так называемую схему прогноза
| y4=4hf(x3,y3)+(y0-10y3)/3-2y1+6y2, | (7.32) |
которую и можно использовать в качестве начального приближения для решения уравнения (7.30).
Дата добавления: 2018-02-15; просмотров: 506; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
