Решение с помощью рядов Тейлора

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Предположим, что нами уже найдено приближенное решение уравнения (7.2) для точек x_0, x_1, x_{2, . . . ,} x_m. При этом последовательные значения x_i расположены на расстоянии h друг от друга, т.е. x_i+1 = x_i + h.

Разложим искомую функцию y(x) в ряд Тейлора в окрестности точки x_m:

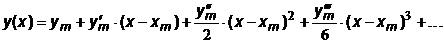где 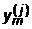- значение j -й производной от функции y(x), вычисленное в точке x = x_m.

Найдем приближенное значение y_m₊₁ для точки x_m₊₁, подставив в это разложение вместо x величину x_m₊₁ :

(7.3)

Чем больше членов этого ряда мы возьмем для вычисления, тем точнее будет решение.

Из (7.2) имеем: 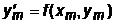. Дифференцируя обе части (7.2) по x и учитывая, что y есть функция от x, получаем:

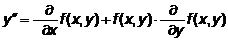
или для сокращения записи: 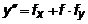, где f_x, f_y - частные производные от функции по x и y соответственно.

Тогда выражение (7.3) приобретает вид:

(7.4)

где O(h³) означает, что в следующие (отброшенные) члены ряда значение h входит в степени не ниже третьей.

Таким образом, если для решения уравнения (7.2) будет использована формула (7.4), то погрешность усечения будет приблизительно равна Ch³, где C - некоторая постоянная, не зависящая от h.

Решение дифференциального уравнения данным способом является одноступенчатым, так как для вычисления каждого y_m₊₁ требуется информация только об одной предыдущей точке (x_m, y_m).

С практической точки зрения трудность использования этого метода заключается в необходимости нахождения и вычисления частных производных f_x, f_y, что в некоторых ситуациях бывает просто невозможно. Кроме того, если попытаться получить лучшее приближение, то необходимо вычислять уже третью производную:

Производные более высоких порядков становятся еще более сложными. На практике этот метод не используется, а здесь он приведен как основа для вывода других методов и оценки их погрешностей.

Метод Эйлера

Это простейший метод решения задачи Коши, позволяющий интегрировать дифференциальные уравнения первого порядка. Его точность невелика, и поэтому на практике им пользуются сравнительно редко. Однако на основе этого метода легче понять алгоритмы других, более эффективных методов.

Итак, решается задача Коши (7.2, 7.2’). Запишем разложение (7.3) для m=0, отбросим в нем члены, содержащие h во второй и более высоких степенях, и получим:

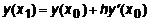(7.5)

Величину находим из дифференциального уравнения (7.2), подставив в него начальное условие: 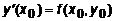. Таким образом можно получить приближенное значение зависимой переменной при малом смещении h от начальной точки.

Этот процесс можно продолжить, используя соотношение

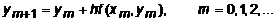
(7.6)

и делая сколь угодно много шагов. Графически метод Эйлера показан на рис.7.3. Хотя тангенс угла наклона касательной к истинной кривой в исходной точке известен и равен y'(x₀), он изменяется в соответствии с изменением независимой переменной. Поэтому в точке x₀+h наклон касательной уже не таков, каким он был в точке x₀. Следовательно, при сохранении начального наклона касательной на всем интервале [x₀,x₁] в результаты вносится погрешность. Ошибка метода имеет порядок h², а сам метод является методом первого порядка, так как в его вычислительной формуле (7.6) параметр h имеет максимальную степень -1.

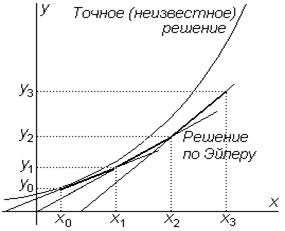Рис.7.3. Геометрическая интерпретация метода Эйлера

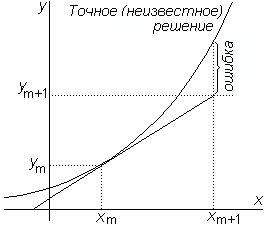Рис.7.4. Ошибка метода Эйлера на m-м шаге

На рис.7.5 представлена блок-схема решения задачи Коши по методу Эйлера

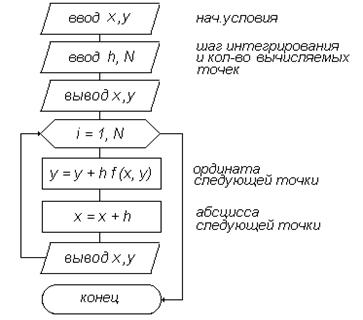
Рис.7.5. Алгоритм метода Эйлера

Дата добавления: 2018-02-15; просмотров: 522; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!