Одношаговые методы решения задачи Коши

Стр 1 из 5Следующая ⇒

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Задача Коши

Обыкновенное дифференциальное уравнение порядка n имеет вид:

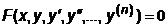
(7.1)

где 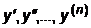⁾- производные первого, второго, ... , n -го порядков от искомой функции y. Его решением является семейство функций

y = y(x,a₁, a₂, ... , a_n),

где a₁, a₂, ... , a_n - произвольные константы.

Например, простейшее дифференциальное уравнение 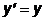имеет решение y = ae^x (рис.7.1). Каждому какому угодно значению параметра a соответствует своя функция, и все эти функции удовлетворяют исходному уравнению.

Рис.7.1. Семейство кривых - решение дифференциального уравнения y' = y

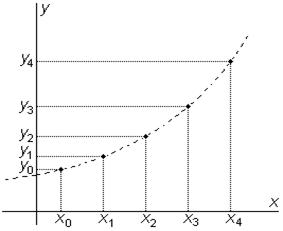Рис.7.2. Результат численного решения задачи Коши

Если в дополнение к уравнению (7.1) задать конкретные значения

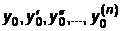
для некоторого значения x₀ в виде

;

;...;

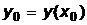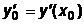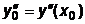(7.1’)

то тем самым определяется конкретный набор a₁, a₂, ... , a_n и, следовательно, единственная конкретная функция y(x,a₁, a₂, ... , a_n) из всего семейства решений.

Условия (7.1') называются начальными условиями, а вся задача, включающая дифференциальное уравнение (7.1) и начальные условия (7.1'), называется "задачей Коши".

К сожалению, класс дифференциальных уравнений, позволяющих аналитическими методами получить решение, довольно узок. Например, уравнение y' = x² + y²не имеет аналитического решения. В большинстве практических задач функция F или коэффициенты, входящие в нее, могут содержать существенные нелинейности или даже задаваться в виде таблиц экспериментальных данных, и тогда аналитическое решение задачи Коши становится невозможным.

При численном решении задачи Коши необходимо задаваться границами x_нач, x_кон изменения аргумента x и величиной h, являющейся шагом его изменения, который определяет дискретность вычисления значений функции y = y(x).

Решение, полученное численным методом, есть таблица соответствующих значений (x_i,y_i), i = 0,1,2,...,n, где x₀=x_нач, x_n= x_кон; x_i+1= x_i+ h (см.рис.7.2).

Поскольку численное решение задачи Коши широко применяется в различных областях науки и техники, то оно в течение многих лет было объектом пристального внимания и число разработанных для него методов очень велико. Здесь мы остановимся на следующих двух группах методов решения задачи Коши.

1. Одношаговые методы, в которых для нахождения каждой новой точки на кривой y=y(x) требуется информация лишь об одном предыдущем шаге. Одношаговыми являются метод Эйлера и методы Рунге-Кутта.

2. Методы прогноза и коррекции (многошаговые методы), в которых для отыскания каждой следующей точки кривой y=y(x) требуется информация более чем об одной из предыдущих точек. К этой группе относятся методы Адамса, Гира и т.д.

Погрешности

Прежде чем перейти к обсуждению конкретных методов численного решения дифференциальных уравнений, остановимся на источниках погрешностей, связанных с численной аппроксимацией. Таких источников три:

1. Погрешность округления обусловлена ограничениями на представление чисел в используемой ЭВМ, так как для любой из них число значащих цифр, запоминаемых и используемых в вычислениях, ограниченно.

2. Погрешность ограничения (усечения) связана с тем, что для аппроксимации функции вместо бесконечных рядов часто используются лишь несколько первых ее членов. Это обычный для численных методов прием, являющийся источником погрешностей, целиком обусловленных применяемым методом и не зависящих от характеристик самой ЭВМ.

3. Погрешность распространения является результатом накопления погрешностей, появившихся на предыдущих этапах счета. Так как ни один приближенный метод не может дать совершенно точных результатов, то любая возникшая в ходе вычислений погрешность сохраняется и на последующих стадиях счета.

Указанные три источника погрешностей являются причиной наблюдаемых ошибок двух типов:

1. Локальная ошибка - сумма погрешностей, вносимых в вычислительный процесс на каждом шаге вычислений.

2. Глобальная ошибка - разность между вычисленным и точным значением величины на каждом этапе реализации численного алгоритма, определяющая суммарную погрешность, накопившуюся с момента начала вычислений.

Одношаговые методы решения задачи Коши

Одношаговые методы рассмотрим на примере решения обыкновенного дифференциального уравнения первого порядка вида

y' = f (x,y) ,

(7.2)

при начальном условии

y(x₀) = y₀.

(7.2’)

С помощью этих методов вычисляют последовательные значения y, соответствующие дискретным значениям независимой переменной x.

Дата добавления: 2018-02-15; просмотров: 754; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 Следующая ⇒

Мы поможем в написании ваших работ!